Research on service life prediction of closely spaced array hole column laminated cooling structure
-
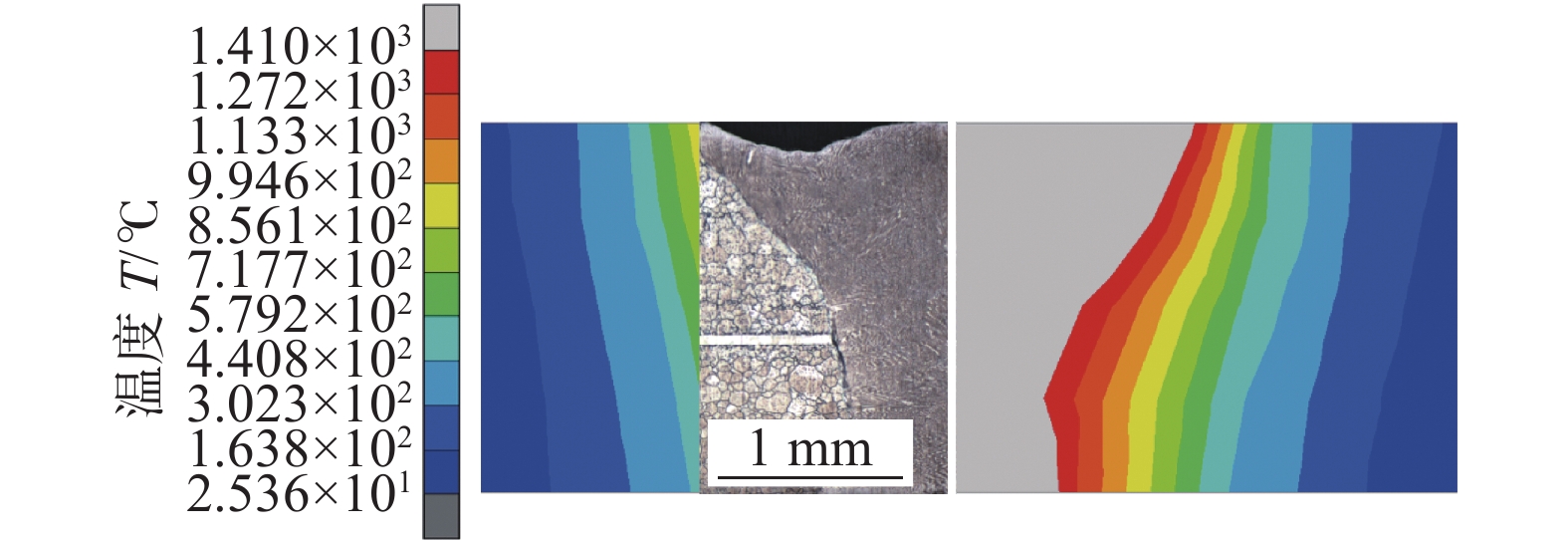
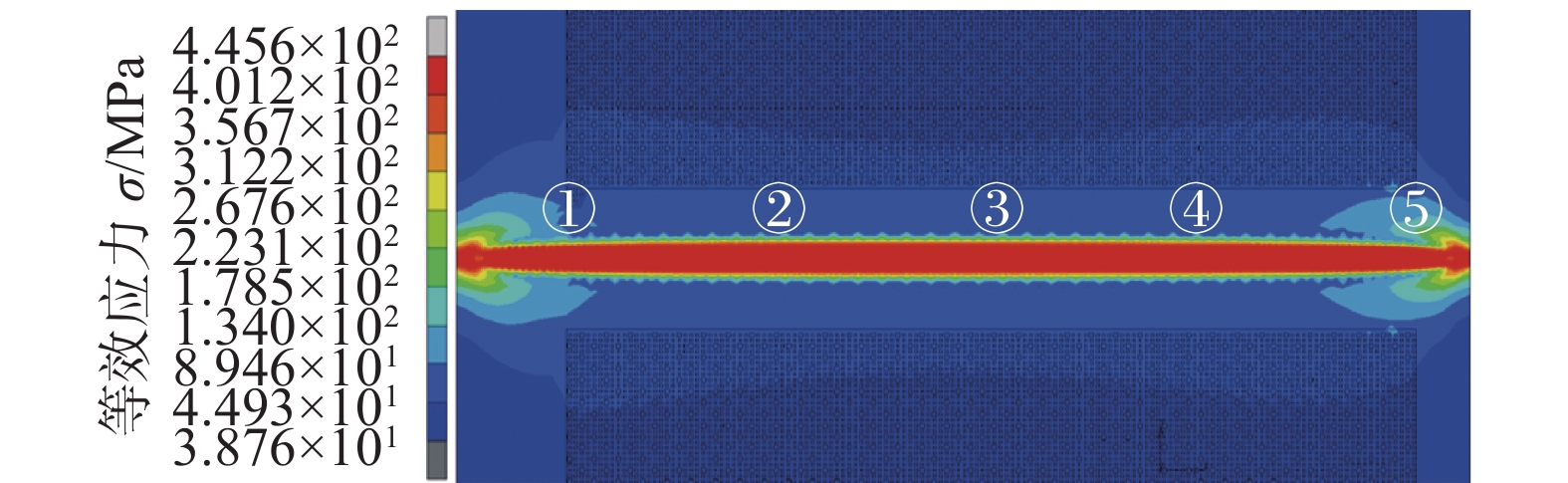
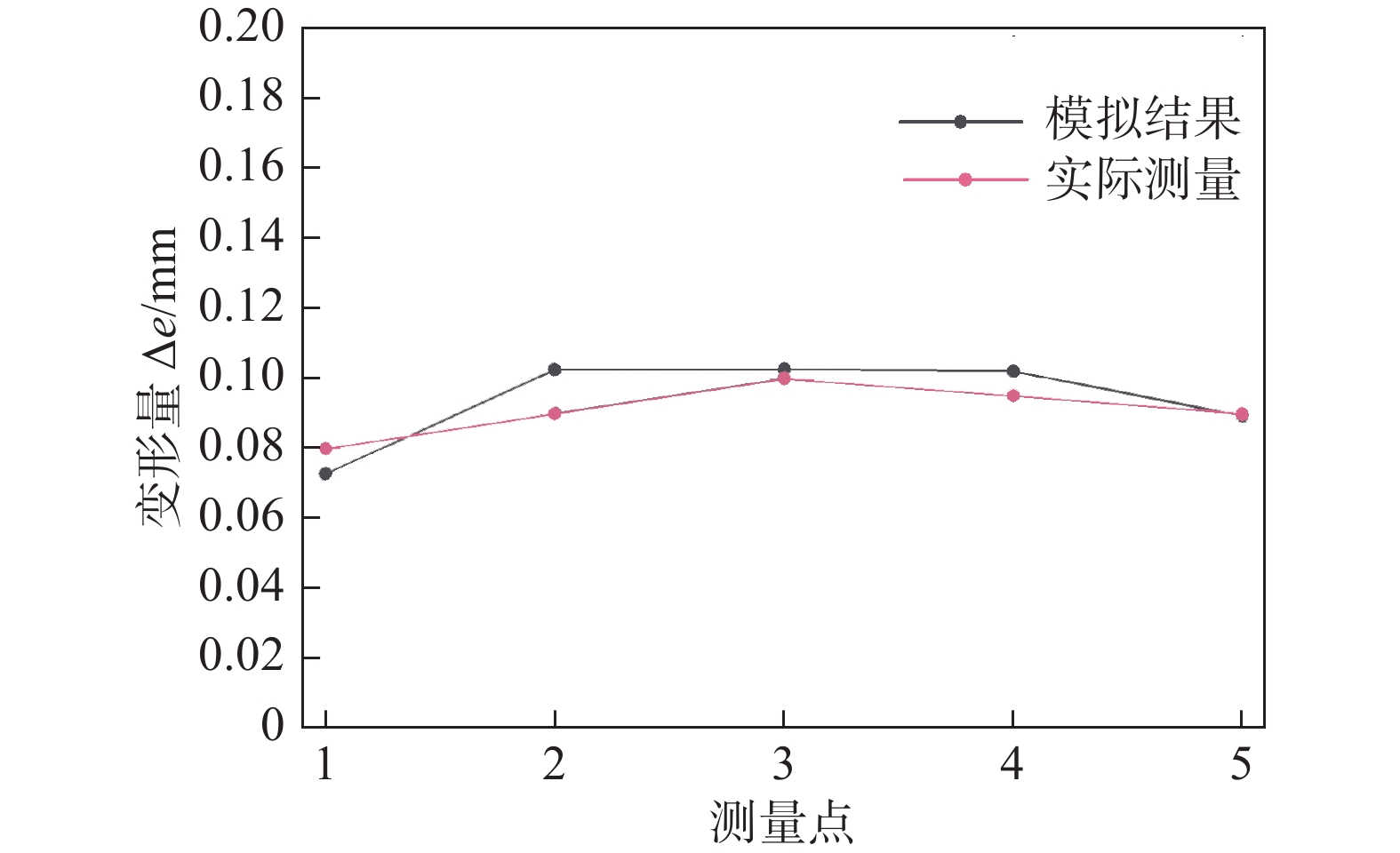
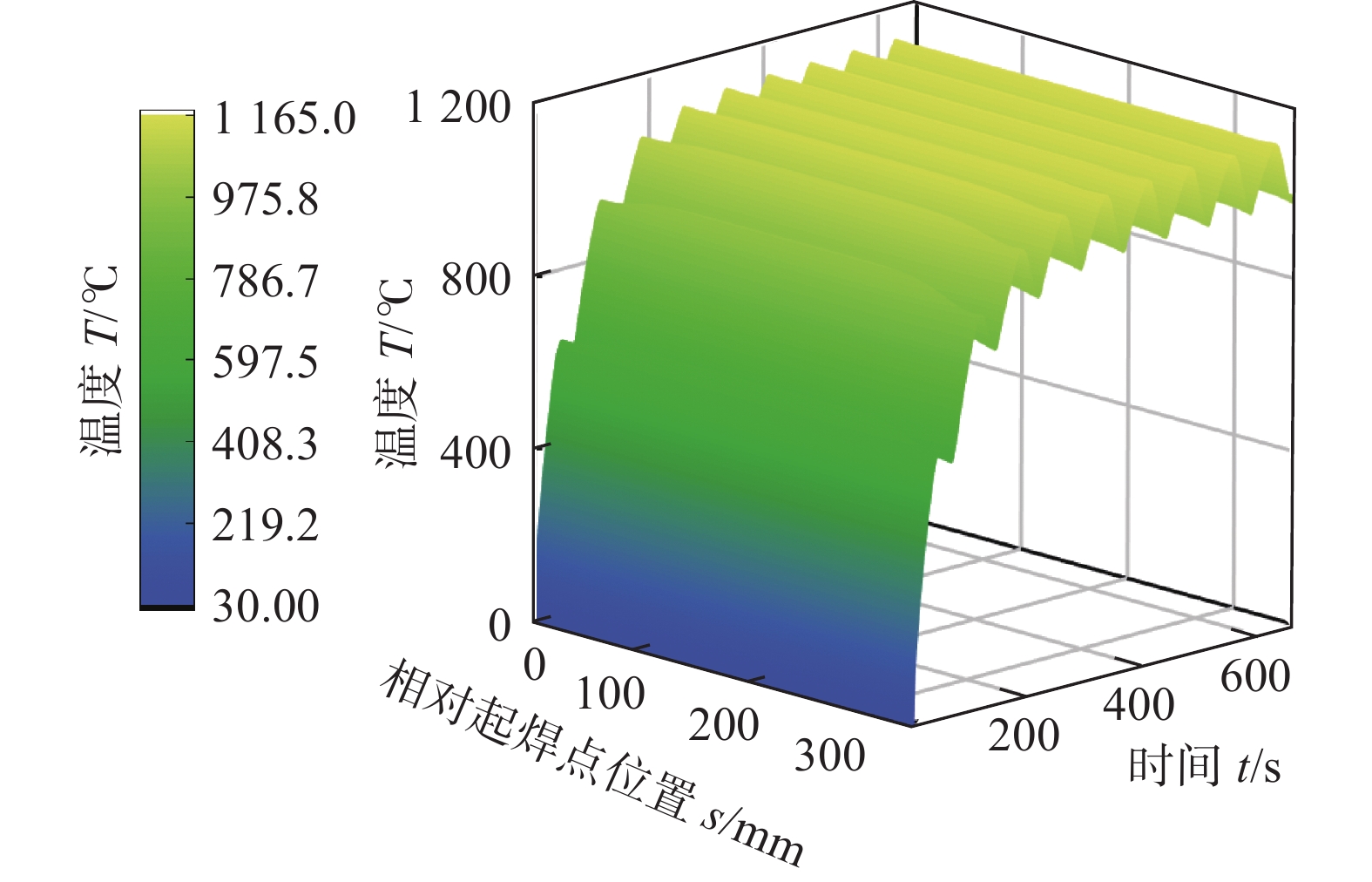
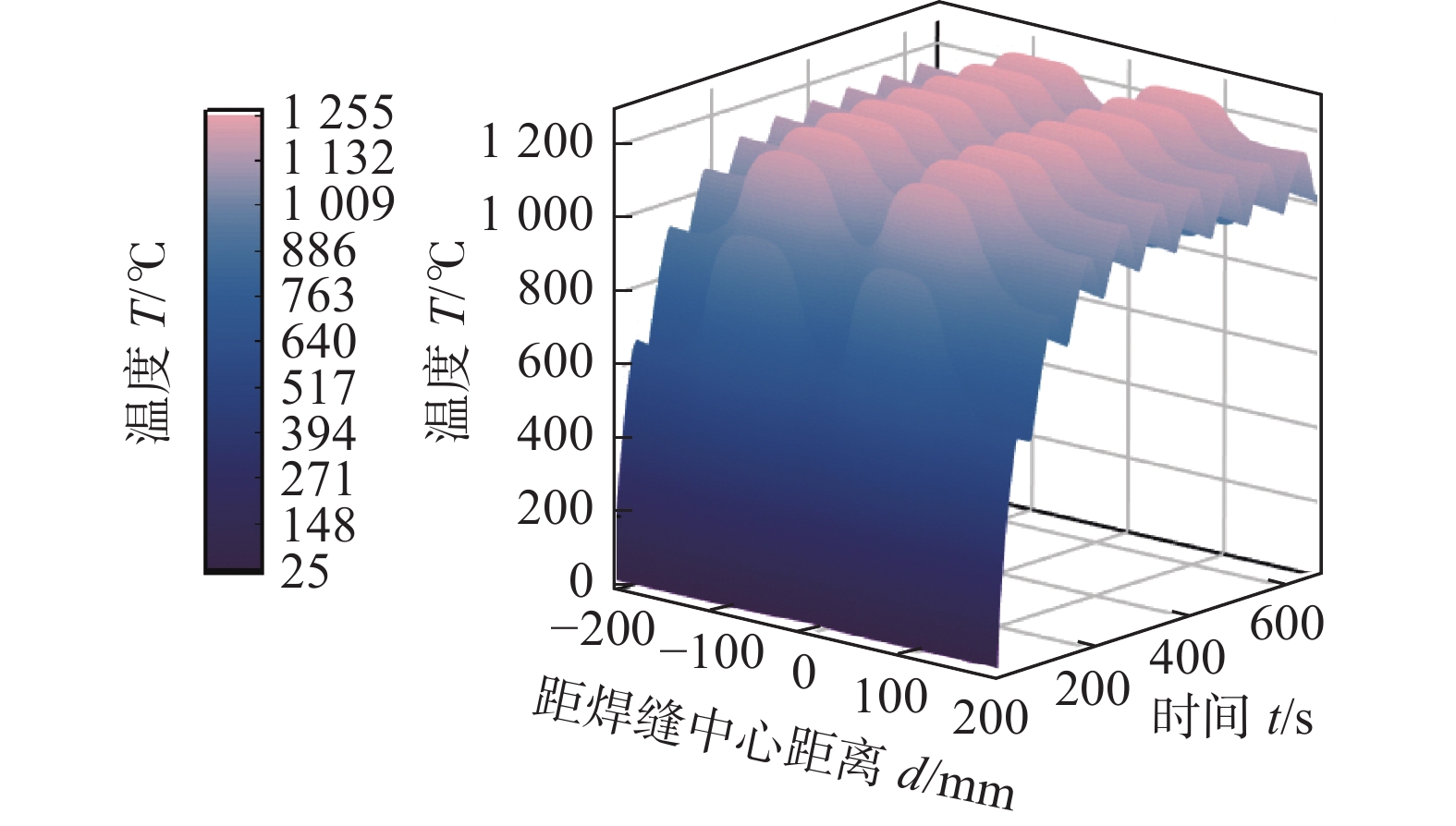
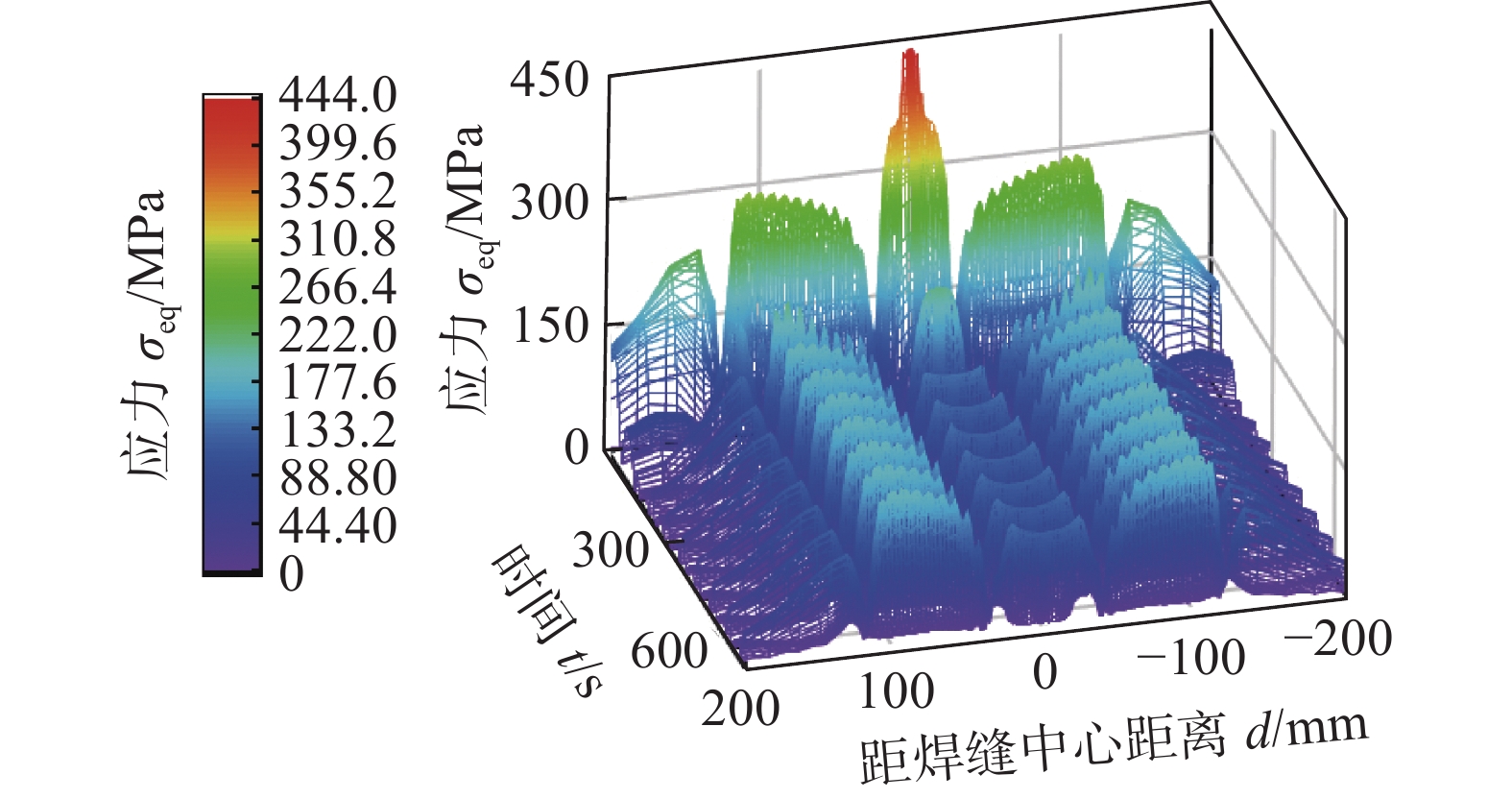
摘要: 层板冷却结构的服役可靠性直接影响发动机的使用安全,利用数值模拟方法分析了典型的密排阵列孔柱层板冷却结构,激光焊接过程及服役过程中温度和应力场分布规律,并依据模拟结果利用Morrow修正的Manson-Coffin公式进行了层板冷却结构的热疲劳寿命评估. 结果表明,层板孔道区域服役状态受焊接残余应力的影响很小,而服役过程对其影响较大,热应力幅值在孔道及附近区域达到最大,为焊缝区域热应力幅值的1.6倍,属于服役过程中的危险区域,预估此处的疲劳寿命受热疲劳影响较大,为此类结构实际应用中应重点关注的关键区域.Abstract: The service reliability of the laminar cooling structure directly affects the service safety of the engine. In this study, numerical simulation method was used to analyze the distribution of temperature and stress field in the laser welding process and service process of the typical closely spaced array hole column laminar cooling structure. According to the simulation results, the thermal fatigue life of the laminar cooling structure was evaluated by using the Morrow modified Coffin-Manson formula. The results show that the service state of the laminar passage area was little affected by the welding residual stress, but the service process has a great impact on it. The thermal stress amplitude in the laminar passage and nearby area reached the maximum, which was 1.6 times of the thermal stress amplitude in the weld area. It belongs to the dangerous area in the service process. It is estimated that the fatigue life here is greatly affected by thermal fatigue, which should be paid attention to in practical application.
-
Keywords:
- laminar cooling structure /
- residual stress /
- thermal stress /
- fatigue life
-
0. 序言
焊接结构钢板广泛应用于航空航天、石油储罐和管道运输等工业领域[1-3]. 焊接结构钢板焊接质量往往取决于焊接工艺参数和焊接环境,在其生产加工和使用过程中,难免会产生一些无法用肉眼看见的损伤或缺陷,如腐蚀、裂纹和应力破裂等,有必要对其定期进行无损检测[4]. 超声导波成像检测方法传播距离远、衰减小,广泛应用于工业无损检测与结构健康监测中[5-6].
超声阵列成像检测中,常用的阵列型式有直线阵列和非阵列等典型形式[7]. 合成孔径阵列超声导波成像检测相关研究表明,发射孔径由不同发射阵元构成,描述发射孔径时往往用发射孔径包含的特定阵元数来表达[8]. 在“一发多收”合成孔径阵列中,某一特定发射阵元构成发射孔径,多个接收阵元构成接收孔径. 接收矩阵含有成像信息,接收孔径接收到的成像数据可用接收矩阵来表达,接收矩阵是研究超声导波合成孔径直线阵列成像的有力工具,接收矩阵的秩与接收阵元数相对应[7]. 在“一发多收”阵列中,多个不同的发射阵元发射声波信号后,其回波被满秩接收孔径接收,就可形成多帧满秩成像[9]. 与之相对应地,多个不同的发射阵元发射声波信号后,其回波被变秩接收孔径接收,就将形成多帧变秩成像,可从阵列不同方位视角对同一散射声场中不同散射信息分别加以重点表征.
在对焊接结构板进行检测时,当两缺陷相距较近或具有焊缝结构时,缺陷反射回波会产生部分重叠或散射,声波衰减较大,影响成像质量[7]. 甚至无法直接从成像结果中分辨缺陷,可通过对阵列参数进行优化,对阵元接收的板中导波信号进行多点聚焦,用来补偿声波因材料厚度或材料引起的波的色散[10],以增强导波信号[11]. 针对碳纤维增强树脂基复合材料层压板分层缺陷的准确识别问题,通过对相控阵超声激活孔径进行优化选择,有效提高缺陷检测精度[12]. 针对焊缝内粗大柱状晶引起的超声波散射和晶粒取向不同导致的声束偏折问题,可采取时间反转算子分解超声阵列信号全矩阵数据分离噪声进行信号增强. 对于单一板中超声导波,运用波幅矩阵和渡时矩阵,对弧形阵列接收数据矩阵信息进行多帧满秩成像,图像SNR得到了不同程度增大[9, 13]. 以上研究工作可为焊接结构超声导波成像检测研究与应用提供有益借鉴. 然而,在对焊接结构进行超声导波成像检测中,焊缝散射的存在,使得成像受到很大影响[14]. 也就是说,焊接结构中焊缝散射条件下,当接收孔径为变秩接收孔径时,多帧变秩成像的规律和机理尚待进一步研究.
文中提出将超声导波合成孔径直线阵列多帧变秩成像,用于焊接结构板中缺陷检测研究. 针对焊接结构板中直线合成孔径阵列,研究了焊缝散射条件下超声导波多帧变秩成像机理,可为丰富与发展超声导波阵列成像检测的研究与应用提供重要基础.
1. 成像检测理论与试验方法
1.1 超声导波合成孔径成像
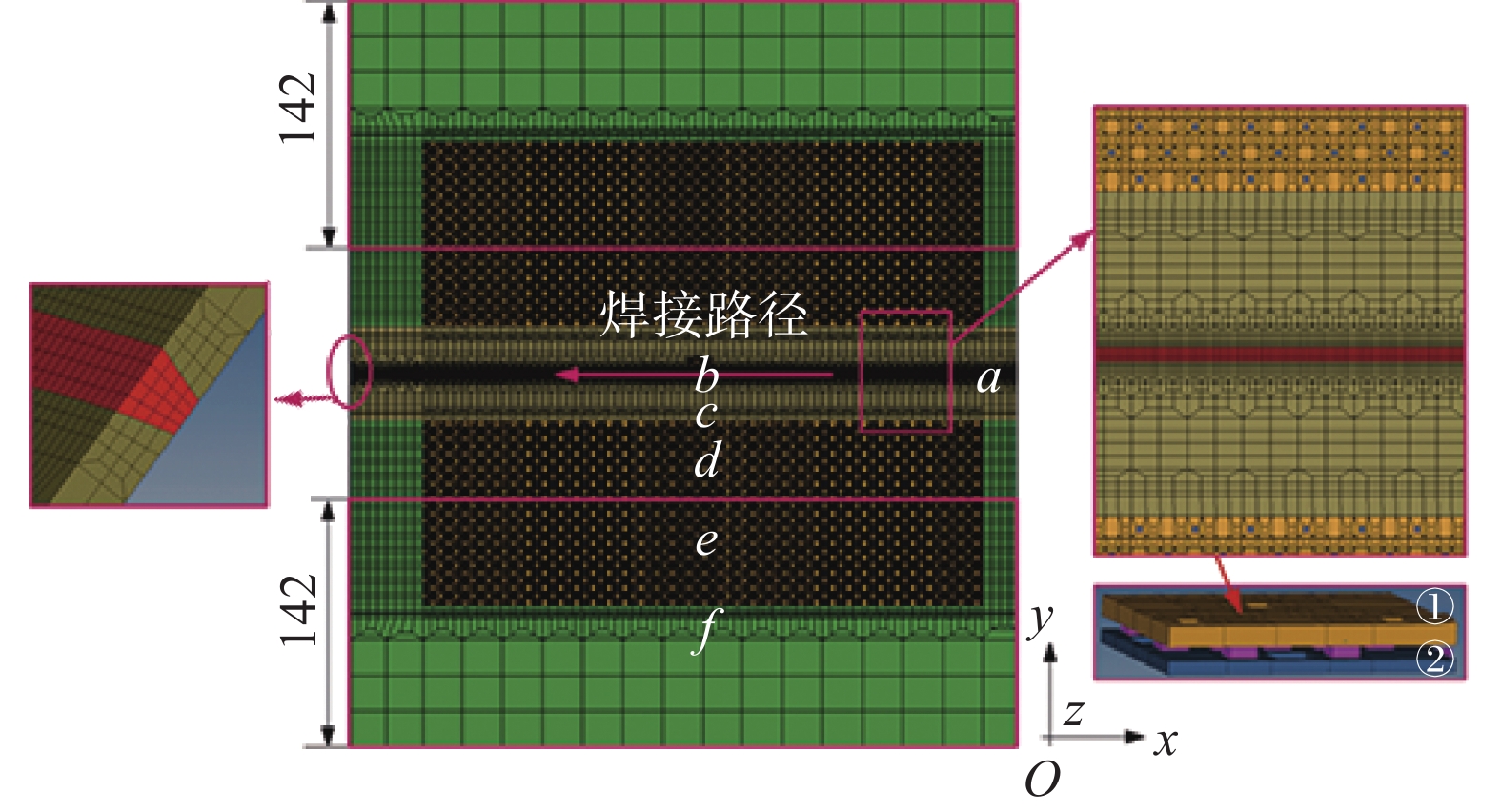
超声导波具有多个模态,在导波信号中形态表现为“多个波包”. 对特定模态的导波来说,散射体回波“波包”中峰值较为明示且集中,有利于进行成像. 合成孔径成像是通过将不同位置小孔径(或阵元)同相位回波信号合成为一个大孔径信号,获得更高SNR和分辨率的超声图像,增强缺陷定位、定量精度. 设二维声场中空间任一散射点P(x, y), $ \left( {{x_m},{y_m}} \right) $为发射阵元m的坐标,$ \left( {{x_n},{y_n}} \right) $为接收阵元n的坐标,cg为声波在目标区域中传播速度. 超声合成孔径成像示意图,如图1所示. 1号阵元、2号阵元和3号阵元,直至16号阵元构成了直线阵列,dm与dn分别为m号阵元和n号阵元到散射点P(x, y)的距离.
换能器发射导波信号,对于合成孔径阵列而言,第m个阵元为发射阵元,第n个阵元为接收阵元,则其发射接收时间为
$$ \left\{\begin{split} &{t_{m,n}}(P) = \frac{{{d_m}(P) + {d_n}(P)}}{{{c_g}}} \\&{{\text{d}}_m}(P) = \sqrt {{{({x_m} - x)}^2} + {{({y_m} - y)}^2}}\\& {{\text{d}}_n}(P) = \sqrt {{{({x_n} - x)}^2} + {{({y_n} - y)}^2}} \end{split}\right. $$ (1) 式中:dm (P)为m阵元发射到P点的传播距离;dn(P)为n阵元接收P点反射声波传播的距离.
阵列中相邻阵元的延时时间为
$$ t_{m,n}^d(p) = {(\Delta t)_{\max }} - {t_{m,n}}(p) $$ (2) 式中:$ {(\Delta t)_{\max }} $为阵列中阵元到聚焦点P的最大传输时间.
对各阵元声场进行叠加计算,可得到总声场数据矩阵,理想单一频率成分的阵元发射信号的叠加为
$$ {B_{{\mathrm{SAFT}}}}({d_m},\theta ) = \sum\limits_{n = 0}^N {{{\text{e}}^{{\text{j}}{\omega _0}\left( - \tfrac{{2{d_m}}}{{{c_g}}} - {t_{m,n}}\right)}}} $$ (3) 式中:θ为发射阵元相对散射点偏转角度;dm为第m个发射阵元到散射体的距离;tm,n为声波传播时间;cg为板中声波群速度.
当阵列参数确定后,孔径大小是影响阵列声场特性的重要参数,进而影响成像分辨率. 实际换能器作为阵元发射信号时,其声波是多种频率成分且有一定频带宽度的信号. 特定频带宽度的换能器作为阵列阵元发射接收导波的合成孔径信号为
$$ {B_{{\mathrm{SAFT}}}}({d_m},\theta ) = \sum\limits_{n = 1}^N \left[\int_{{\omega _1}}^{{\omega _2}} {{{\text{e}}^{{\text{j}}\omega \left( - \tfrac{{2{d_m}}}{{{c_g}}} - {t_{m,n}}\right)}}d\omega } \right] $$ (4) 式中:$ {\omega _1} $为信号下限频率f1对应的角频率,取2πf1;$ {\omega _2} $为信号上限频率f2对应的角频率,取2πf2.
下限频率f1和上限频率f2取值,如图2所示. 对于超声SH导波而言,超声SH导波回波信号“波包”相对单一,“波包”中的相邻峰值较为集中,特别有利于进行成像检测.
1.2 超声导波直线阵列多帧变秩成像
在无焊缝结构单一板材的超声导波合成孔径多帧变秩成像中,阵列接收的信号较为简单,不会产生较为复杂的信号. 焊接结构中由于具有焊缝散射,会对超声回波信号的接收产生干扰,影响其成像. 焊接结构超声导波直线阵列多帧变秩成像是指发射孔径一定时,接收孔径中阵元接收发射孔径的信号是不同的,可表达为波幅矩阵和渡时矩阵[9],包含了焊接结构板中阵列成像时可拟利用的所有信息. 超声导波合成孔径直线阵列成像时,假定有N个单一模态超声导波换能器作为阵元构成直线阵列,第m个阵元发射声波被散射体P(x, y)散射后被第n阵元接收到的回波信号$ {X_{mn}}(t) $为
$$ \begin{split} & {X_{mn}}(t) = {\left( {{x_{m0}}(t)\cdots {x_{mn}}(t)\cdots {x_{mN}}(t)} \right)^{\mathrm{T}}} \\& \qquad\qquad(m,n = 1,2,3\cdots N) \end{split}$$ (5) 令散射体回波信号中某一具有周期信号的主峰值在$ {X_{mn}}(t) $中为Amn,其主峰值对应的渡越时间为Tmn,当阵元m发射声波,接收孔径阵元数为s,在发射孔径不变前提下,当接收孔径阵元数变化时,对应的接收矩阵的秩也变化,称之为变秩接收孔径. 当具有焊缝结构时,板中导波的波幅矩阵AmN[14]为
$$ \begin{gathered} {A_{mN}} = {[{a_1} \cdots {a_s} \cdots {a_N}]^T}= \\ \left[ {\begin{array}{*{20}{c}} {{A_{1,{\text{1}}}}}& \cdots &{{A_{1,s}}\begin{array}{*{20}{c}} \cdots \end{array}} \\ \vdots & & \vdots \\ {{A_{s{\text{,1}}}}}& \cdots &{{A_{s,s}}\begin{array}{*{20}{c}} \cdots \end{array}} \\ \vdots & & \vdots \\ {{A_{N,{\text{1}}}}}& \cdots &{{A_{N,n}}\begin{array}{*{20}{c}} \cdots \end{array}} \end{array}\begin{array}{*{20}{c}} {{A_{1,N}}}& \cdots &{{A_{1,k(N + 1) - 1}}} \\ & \vdots & \vdots \\ {{A_{s,N}}}& \cdots &{{A_{s,k(N + 1) - 1}}} \\ & \vdots & \vdots \\ {{A_{N,N}}}& \cdots &{{A_{N,k(N + 1) - 1}}} \end{array}} \right] \\ \end{gathered} $$ (6) 式中:m为发射阵元数;N为接收孔径阵元数;k为焊缝散射因子,表示散射体回波信号“波包”峰值的个数.
焊缝散射造成缺陷信号“多峰”,这时焊缝散射因子k>1,破坏了成像检测信号的椭圆簇曲线阵列特征,造成了成像质量劣化[14],这是影响成像清晰度的重要因素. 此时,焊缝散射条件下阵列信号波幅矩阵$ A_{^{N,k(N + 1) - 1}}^w $为
$$A_{N, k(N+1)-1} = \left[ \begin{array}{ccccc} A_{1,(s+1)} & \cdots & A_{1,(s+k)} & \cdots & A_{1, k(N+1)-1} \\ \vdots & & \vdots & & \vdots \\ A_{u,(s+1)} & \cdots & A_{u,(s+K)} & \cdots & A_{u, k(N+1)-1} \\ \vdots & & \vdots & & \vdots \\ A_{N,(s+1)} & \cdots & A_{N,(s+K)} & \cdots & A_{N, k(N+1)-1} \end{array} \right] $$ (7) 与波幅矩阵对应的渡时矩阵$ T_{N,k(N + 1) - 1}^w $为
$$ \boldsymbol{T}_{N, k(N+1)-1}=\left[\begin{array}{ccccc} t_{1,(\mathrm{~s}+1)} & \cdots & t_{1,(s+k)} & \cdots & t_{1,(k(N+1)-1)} \\ \vdots & & \vdots&& \vdots \\ t_{u,(s+1)} & \cdots & t_{u,(s+k)} & \cdots & t_{u,(k(N+1)-1)} \\ \vdots & & \vdots&& \vdots \\ t_{N,(s+1)} & \cdots & t_{N,(s+k)} & \cdots & t_{N,(k(N+1)-1)} \end{array}\right] $$ (8) 显然,波幅矩阵与渡时矩阵的秩R相等,且有
$$ R = R\left( {T_{^{N,k(N + 1) - 1}}^{\text{T}}} \right) = R\left( {A_{^{N,k(N + 1) - 1}}^{\text{T}}} \right) = s + N(k - 1)$$ (9) 波幅矩阵与渡时矩阵统称为接收矩阵. 接收矩阵的秩R,反映了接收孔径和接收孔径的大小. 无焊缝散射时,焊缝散射因子k = 1,式(9)中接收矩阵的秩R等于接收阵元数s;当有焊缝散射时,焊缝散射因子k>1,式(9)描述了焊缝散射的相关信息,此时,接收矩阵的秩R大于接收阵元数s. 从导波合成孔径阵列成像算法和成像机理出发,接收矩阵为导波阵列成像提供了幅值和渡越时间信息. 结合文献[14]可知,在分析超声SH导波直线阵列成像所特有的椭圆簇轨迹特征基础上,可将接收矩阵用于描述焊缝散射.
当N个阵元发射声波信号,接收矩阵的秩为R时,接收孔径阵元接收回波信号为
$$ {B_{{\mathrm{SAFT}}}}(R) = \sum\limits_{m = 1}^N {\sum\limits_{n = 1}^R \left[\int_{{\omega _1}}^{{\omega _2}} {{{\text{e}}^{{\text{j}}\omega \left( - \tfrac{{2{d_m}}}{{{c_g}}} - {t_{m,s}}\right)}}d\omega } \right]} $$ (10) 成像区域内任一点反射回波信号转换为该散射体相应像素点的灰度g(R, x, y),那么焊接结构板中超声导波直线阵列多帧变秩成像为
$$ \begin{split} & g(R,x,y) = 25{\text{6}} \times \frac{{{B_{{\mathrm{SAFT}}}}(R) - {P_{\min }}}}{{{P_{\max }} - {P_{\min }}}} =\\& 25{\text{6}} \times \frac{{\displaystyle\sum\limits_{m = 1}^N {\displaystyle\sum\limits_{n = 1}^R \left[\int_{{\omega _1}}^{{\omega _2}} {{{\text{e}}^{{\text{j}}\omega \left( - \tfrac{{2{d_m}}}{{{c_g}}} - {t_{m,s}}\right)}}d\omega } \right]} - {P_{\min }}}}{{{P_{\max }} - {P_{\min }}}} \end{split} $$ (11) 式中:Pmax为成像区域中所有散射点中的最大回波幅信号幅值;Pmin为成像区域中所有散射点中的最小回波幅值.
式(11)所表达的图像具有256级灰度. 焊缝散射条件下进行超声导波多帧变秩成像实施时,对于焊缝散射因子k > 1时,对焊缝散射导致的多个“波包”峰值进行取值. 可以看出,当超声导波直线阵列多帧变秩成像时,接收孔径改变时,接收矩阵及其秩也相应改变.
1.3 成像检测试验系统
为验证超声导波直线阵列多帧变秩成像检测的可行性,构建了焊接板结构超声导波直线阵列多帧变秩成像检测系统,如图3所示,系统由成像处理器、数据采卡、脉冲信号发射接收器、具有对接焊缝的焊接结构钢板试样和直线阵列等构成,其中超声SH导波换能器作为阵元构成直线阵列,换能器[15]是课题组为了开展超声导波多帧变秩成像检测研究先行特别研制,阵列阵元数为16,阵元间距为50 mm,超声导波换能器中心频率为0.65 mHz,所激发导波以SH0模态为主,波长约为4.9 mm. 焊接结构钢板的尺寸为
2250 mm ×1000 mm × 4 mm, 钢板中人工通孔缺陷孔A、孔B、孔C和孔D的直径分别为5,8,10 mm和12 mm. 当声波经过对接焊缝时形成焊缝散射条件,焊缝形貌如图4所示.2. 试验结果与分析
根据式(11)针对图3系统进行焊缝散射条件下超声导波直线阵列多帧变秩成像检测试验,得到多帧变秩图像,如图5所示. 图5中当接收矩阵的秩R为4,8,12和16所对应的图像,与波长尺寸相当的人工缺陷孔A、孔B、孔C和孔D均得到了较好显示. 当接收孔径发生变化时,接收矩阵的秩相应发生变化,成像区域内接收矩阵数据也会发生变化. 当发射孔径不变,接收矩阵的秩改变时,就形成了不同的多帧变秩图像. 从这些图像中可清晰显示人工缺陷信息,成像效果总体较好,焊缝由于焊缝散射回波强,图像灰度特别高.
当发射孔径不变、接收孔径变化时,直线阵列多帧变秩所成图像灰度有所不同,如图6所示,当接收矩阵的秩R变化时,孔A的灰度从R = 4开始整体上呈现为逐渐下降趋势,孔B的灰度整体基本保持不变,孔C和孔D的灰度整体上呈现递增趋势. 随着接收矩阵的秩R的变化,图像的背景灰度也在变化. 这里暂以缺陷为中心、取10倍波长区域内灰度值平均值作为缺陷的背景灰度,如图7所示,孔A、孔B和孔D缺陷的背景灰度总体上变化幅度不大. 但孔C由于距焊缝较近,焊缝散射对孔C影响较大,使孔C背景灰度大体呈现逐渐增加趋势. 稳定的背景灰度,有利于图像中缺陷信息的显示.
图像SNR是图像的另一主要特征,SNR越大,图像对缺陷信息的表征效果越好. 超声导波直线阵列多帧变秩图像的SNR,如图8所示. 随着接收矩阵的秩R的增加,图像SNR呈现整体上升趋势,特别是孔C和孔D的SNR整体呈现逐渐增大的趋势特别明显. 但以个别缺陷来说,SNR的变化细节略有差异. 在接收矩阵的秩R增大的前半程,孔A和孔B的SNR呈现准单调递增,当接收矩阵的秩R为7时,孔A的SNR达到最大,出现“拐点”,之后,SNR逐渐降低. 值得一提的是,随着接收矩阵的秩R的增大,从总体上看,多帧变秩图像SNR得到了增大,但在半满秩时,SNR曲线均出现“准拐点”,增大放缓,当接收矩阵的秩R为8时,整体的“准拐点”出现. 考虑到成像实际,从整体分析来看,接收矩阵的秩R约为10时,也就是接收矩阵的秩R约为满秩的2/3时,整体成像效果较好. 经过分析,这时多帧变秩图像的缺陷灰度值比非变秩图像增大28.7%;当然,此时的多帧变秩成像运算效率也得到了提高.
3. 结论
(1)分析了超声导波直线合成孔径成像,提出焊缝散射条件下超声导波直线阵列多帧变秩成像检测方法,探讨了焊缝散射条件下超声导波直线阵列多帧变秩成像机理.
(2)理论分析表明,作为接收矩阵的波幅矩阵与渡时矩阵具有相同的秩,随着接收矩阵的秩的变化,接收孔径相应改变,直接表现为接收阵元数的变化.
(3)在超声导波直线阵列多帧变秩成像中,焊缝散射因子可用来表征散射. 随着接收矩阵的秩的增大,超声导波直线阵列多帧变秩图像的灰度和SNR得到不同程度增大,满秩的2/3时SNR曲线出现拐点,这时成像效果较好. 成像检测试验与理论分析互相得到了验证,将超声导波直线阵列多帧变秩成像用于焊接结构进行检测具有较好的可行性.
-
表 1 合金热物性参数
Table 1 Alloy thermophysical parameters
温度T/℃ 弹性模量E/GPa 屈服强度ReL/MPa 热膨胀系数 $\alpha $ /K−1热导率 $\lambda $ /(W·m−1·K−1)比热容c/(J·g−1·K−1) RT 232 470 — 10.4 0.403 100 225 — 11.9 12.2 0.423 200 217 — 12.6 14.3 0.444 300 209 — 13.2 15.9 0.465 400 201 — 13.8 17.5 0.486 500 193 290 14.5 19.3 0.502 600 184 275 15.2 21.1 0.523 700 176 270 15.8 23.0 0.540 800 169 250 16.5 24.8 0.557 900 161 130 17.1 25.5 0.573 1000 153 64 17.9 27.6 0.590 -
[1] 高亚伟, 董建新, 姚志浩, 等. GH5188高温合金组织特征及冷热加工过程组织演变[J]. 稀有金属材料与工程, 2017, 46(10): 2922 − 2928. Gao Yawei, Dong Jianxin, Yao Zhihao, et al. Microstructure characteristics and microstructure evolution during cold and hot working of GH5188 superalloy[J]. Rare Metal Materials and Engineering, 2017, 46(10): 2922 − 2928.
[2] 吴静, 蔡文哲, 王雨龙. 火焰筒热疲劳寿命评估[C]//中国航天第三专业信息网第三十九届技术交流会暨第三届空天动力联合会议, 洛阳. 2018. Wu Jing, Cai Wenzhe, Wang Yulong. Thermal fatigue life assessment of flame tube[C]//The 39th Technical Exchange Conference and the 3rd Aerospace Power Joint Conference of China Aerospace Third Professional Information Network, Luoyang. 2018.
[3] 徐绍桐, 王长辉, 杨成骁. 液体火箭发动机再生冷却结构弹塑性分析[J/OL]. 航空动力学报. DOI: 10.13224/j. cnki. jasp. 20210328. https://doi.org/10.13224/j.cnki.jasp.20210328. Xu Shaotong, Wang Changhui, Yang Chengxiao. Elastoplastic analysis of regenerative cooling structure of liquid rocket engine [J/OL]. Journal of Aerodynamics. DOI:10.13224/j.cnki.jasp.20210328. https://doi.org/10.13224/j.cnki.jasp.20210328.
[4] 吴向宇, 黎旭, 时艳, 等. 典型层板冷却结构热疲劳破坏特性研究[J]. 航空动力学报, 2014, 29(5): 1177 − 1183. doi: 10.13224/j.cnki.jasp.2014.05.025 Wu Xiangyu, Li Xu, Shi Yan, et al. Study on thermal fatigue failure characteristics of typical laminate cooling structures[J]. Journal of Aerodynamics, 2014, 29(5): 1177 − 1183. doi: 10.13224/j.cnki.jasp.2014.05.025
[5] Barrett P R, Ahmed R, Menon M, et al. Isothermal low-cycle fatigue and fatigue-creep of Haynes 230[J]. International Journal of Solids & Structures, 2016, 88-89: 146 − 164.
[6] 易慧. 环形燃烧室火焰筒强度寿命技术研究[D]. 南京: 南京航空航天大学, 2008. Yi Hui. Technical study on strength and life of annular combustor liner [D] Nanjing: Nanjing University of Aeronautics and Astronautics, 2008.
[7] 耿小亮, 郭运强, 张克实, 等. 火焰筒热疲劳分析与寿命估计[J]. 机械强度, 2007, 29(2): 305 − 309. doi: 10.3321/j.issn:1001-9669.2007.02.026 Geng Xiaoliang, Guo Yunqiang, Zhang Keshi, et al. Thermal fatigue analysis and life estimation of flame tube[J]. Mechanical strength, 2007, 29(2): 305 − 309. doi: 10.3321/j.issn:1001-9669.2007.02.026
[8] 张俊红, 戴胡伟, 鲁鑫, 等. 流固耦合作用下航空发动机燃烧室热疲劳研究[J]. 西安交通大学学报, 2018, 52(5): 149 − 156. doi: 10.7652/xjtuxb201805021 Zhang Junhong, Dai Huwei, Lu Xin, et al. Study on thermal fatigue of aeroengine combustion chamber under fluid structure interaction[J]. Journal of Xi'an Jiaotong University, 2018, 52(5): 149 − 156. doi: 10.7652/xjtuxb201805021
[9] 全栋梁, 郁新华, 刘松龄, 等. 层板冷却结构流阻特性的实验与数值模拟[J]. 推进技术, 2003, 24(5): 425 − 428. doi: 10.3321/j.issn:1001-4055.2003.05.010 Quan Dongliang, Yu Xinhua, Liu Songling, et al. Experimental and numerical simulation of flow resistance characteristics of laminar cooling structure[J]. Propulsion Technology, 2003, 24(5): 425 − 428. doi: 10.3321/j.issn:1001-4055.2003.05.010
[10] 郁新华, 全栋梁, 刘松龄, 等. 层板结构内部换热特性的研究[J]. 航空学报, 2003, 24(5): 405 − 410. doi: 10.3321/j.issn:1000-6893.2003.05.005 Yu Xinhua, Quan Dongliang, Liu Songling, et al. Study on the internal heat transfer characteristics of laminated structures[J]. Journal of Aeronautics, 2003, 24(5): 405 − 410. doi: 10.3321/j.issn:1000-6893.2003.05.005
[11] 王鸣, 卢元丽, 吉洪湖. 冲击孔对层板冷却叶片前缘传热影响的数值研究[J]. 航空动力学报, 2013, 28(10): 2240 − 2247. doi: 10.13224/j.cnki.jasp.2013.10.013 Wang Ming, Lu Yuanli, Ji Honghu. Numerical study on the effect of impact hole on the heat transfer at the leading edge of laminated cooling blade[J]. Journal of Aerodynamics, 2013, 28(10): 2240 − 2247. doi: 10.13224/j.cnki.jasp.2013.10.013
[12] 张洁, 武鹏伟, 张东启, 等. 铝合金薄壁箱体焊接应力有限元模拟[J]. 热加工工艺, 2013, 42(3): 203 − 205. doi: 10.14158/j.cnki.1001-3814.2013.03.054 Zhang Jie, Wu Pengwei, Zhang Dongqi, et al. Finite element simulation of welding stress of aluminum alloy thin-walled box[J]. Hot Working Process, 2013, 42(3): 203 − 205. doi: 10.14158/j.cnki.1001-3814.2013.03.054
[13] 杨阳, 邓年春, 郭晓. 钢管混凝土拱桥大管径拱肋环焊缝焊接数值模拟[J]. 焊接学报, 2020, 41(10): 79 − 86, 102. doi: 10.12073/j.hjxb.20200322002 Yang Yang, Deng Nianchun, Guo Xiao. Numerical simulation of girth weld welding of large diameter arch rib of concrete-filled steel tube arch bridge[J]. Transactions of the China Welding Institution, 2020, 41(10): 79 − 86, 102. doi: 10.12073/j.hjxb.20200322002
[14] 唐文书, 肖俊峰, 高松, 等. Nimonic263合金薄板激光焊热源模型及参数研究[J]. 热加工工艺, 2019, 48(19): 131 − 136. doi: 10.14158/j.cnki.1001-3814.2019.19.033 Tang Shi, Xiao Junfeng, Gao Song, et al. Study on heat source model and parameters of laser welding Nimonic263 alloy sheet[J]. Hot Working Process, 2019, 48(19): 131 − 136. doi: 10.14158/j.cnki.1001-3814.2019.19.033
[15] 孙坤, 王洪斌, 张树林, 等. 基于热响应的陶瓷基复合材料火焰筒热冲击试验[J]. 航空发动机, 2021, 47(3): 86 − 90. doi: 10.13477/j.cnki.aeroengine.2021.03.014 Sun Kun, Wang Hongbin, Zhang Shulin, et al. Thermal shock test of ceramic matrix composite flame tube based on thermal response[J]. Aeroengine, 2021, 47(3): 86 − 90. doi: 10.13477/j.cnki.aeroengine.2021.03.014
[16] Tong L W, Huang X W, Zhou F, et al. Experimental and numerical investigations on extremely-low-cycle fatigue fracture behavior of steel welded joints[J]. Journal of Constructional Steel Research, 2016, 119: 98 − 112. doi: 10.1016/j.jcsr.2015.12.015
[17] 童第华, 陈志伟. 局部应变法预测飞机结构带孔部件疲劳寿命[J]. 航空材料学报, 2011, 31(5): 86 − 90. doi: 10.3969/j.issn.1005-5053.2011.5.017 Tong Dihua, Chen Zhiwei. Prediction of fatigue life of perforated components of aircraft structures by local strain method[J]. Journal of Aeronautical Materials, 2011, 31(5): 86 − 90. doi: 10.3969/j.issn.1005-5053.2011.5.017
[18] 麻桃花, 陈金霞. 2219铝合金焊接接头疲劳寿命的计算机预测与试验验证[J]. 热加工工艺, 2016, 45(5): 186 − 189. doi: 10.14158/j.cnki.1001-3814.2016.05.053 Ma Taohua, Chen Jinxia. Computer prediction and experimental verification of fatigue life of 2219 aluminum alloy welded joints[J]. Hot Working Process, 2016, 45(5): 186 − 189. doi: 10.14158/j.cnki.1001-3814.2016.05.053




 下载:
下载: