Effect of stress concentration at weld toes on combined high and low cycle fatigue of EH36 steel welded joints
-
摘要:
为研究船舶结构用钢EH36钢焊接接头焊趾处应力集中对高低周复合疲劳的影响，对不同焊缝形貌20 mm厚EH36钢双面全熔透对接接头进行高低周复合疲劳试验. 研究发现，高低周复合疲劳对接头寿命的降低幅度随着高周应力比的增大而增大；结合数字图像相关法测量结果分析，发现焊趾处应力集中系数越大，接头的高低周复合疲劳寿命越低，其降低幅度随着高周应力比的增大而增大. 基于试验数据对模型进行验证，结果表明，应力集中系数高的接头疲劳寿命低且寿命预测结果分散性增大；Palmgren-Miner模型和Zhu模型由于未充分考虑高低周耦合损伤作用，导致寿命预测结果相对危险. 修正后Zhu模型在充分考虑低周疲劳对高低周复合疲劳寿命的影响后，预测寿命大于实际寿命的预测点较少，预测结果相对安全，且分散性较小，误差也较小.
Abstract:In order to study the effect of stress concentration at the weld toes on combined high and low cycle fatigue(CCF) of EH36 steel welded joints for ship structure, CCF tests were carried out on EH36 steel double-sided butt joints with 20 mm thick and different weld profiles. The results show the extent of reduction in joint life subjected to CCF increased with increasing high stress ratio of high cycle fatigue; Based on the digital image correlation method, the higher the stress concentration coefficient at the weld toes, the lower the CCF life of the joints. The extent of reduction increased with increasing stress ratio of high cycle fatigue. Validation of the models based on experimental data shows that joints with high stress concentration coefficient have lower fatigue life and increased dispersion of life prediction results; The Palmgren-Miner model and Zhu model do not fully consider the CCF damage effect, which leads to dangerous prediction results of CCF life. The modified Zhu model fully considers the influence of CCF. There are few prediction data points that the predicted life is higher than the actual life.The prediction results are relatively safer. The dispersion and the error are smaller.
-
0. 序言
EH36钢为船舶结构用钢，主要应用于大型焊接海洋平台结构[1-2]. EH36钢焊接接头在服役过程中承受周期性波浪载荷引起的高周疲劳(high cycle fatigue, HCF)载荷与装卸载引起的低周疲劳(low cycle fatigue, LCF)载荷的共同作用[3-4]，易发生高低周复合疲劳(combined high and low cycle fatigue, CCF)破坏. 尤其焊趾处由于焊缝几何不连续性产生的应力集中会加速高低周疲劳失效[5- 6]. 焊接接头作为疲劳断裂的关键部位，焊缝倾角、板厚、余高、焊缝宽度和焊趾过渡圆弧半径的作用将导致焊趾处应力集中[7-11]. Tsutsumi等人[12]通过试验和模拟分析研究，发现焊趾处应力集中会导致焊接接头疲劳寿命降低. 因此，应充分重视焊趾对焊接接头高低周疲劳规律的影响及相应的寿命预测和评估.
高低周复合疲劳寿命预测主要采用高周和低周寿命线性叠加模型. 然而，Gan等人[13]通过对船体结构典型焊接接头疲劳寿命研究，发现高低周耦合损伤对疲劳寿命的降低有显著影响. Qiu等人[14]通过高低周应力幅比阈值研究了高低周复合疲劳对寿命的影响，发现高低周耦合损伤加速试样疲劳失效. Zhao等人[15]对TC11钛合金试件高低周复合疲劳试验，发现高周疲劳的平均应力水平和应力比对高低周复合寿命有较大的影响，非线性累积损伤准则的预测效果优于线性累积损伤准则.
目前对于船舶领域钢材焊接结构的高低周复合疲劳的研究较少，且尚未阐明焊缝几何不连续性引起的焊趾处应力集中对高低周复合疲劳寿命的影响. 因此以船舶结构钢为研究材料，对不同焊缝形貌的焊接接头进行高低周复合疲劳试验，研究焊接结构的高低周复合疲劳性能和寿命预测方法具有重大意义.
1. 试验方法
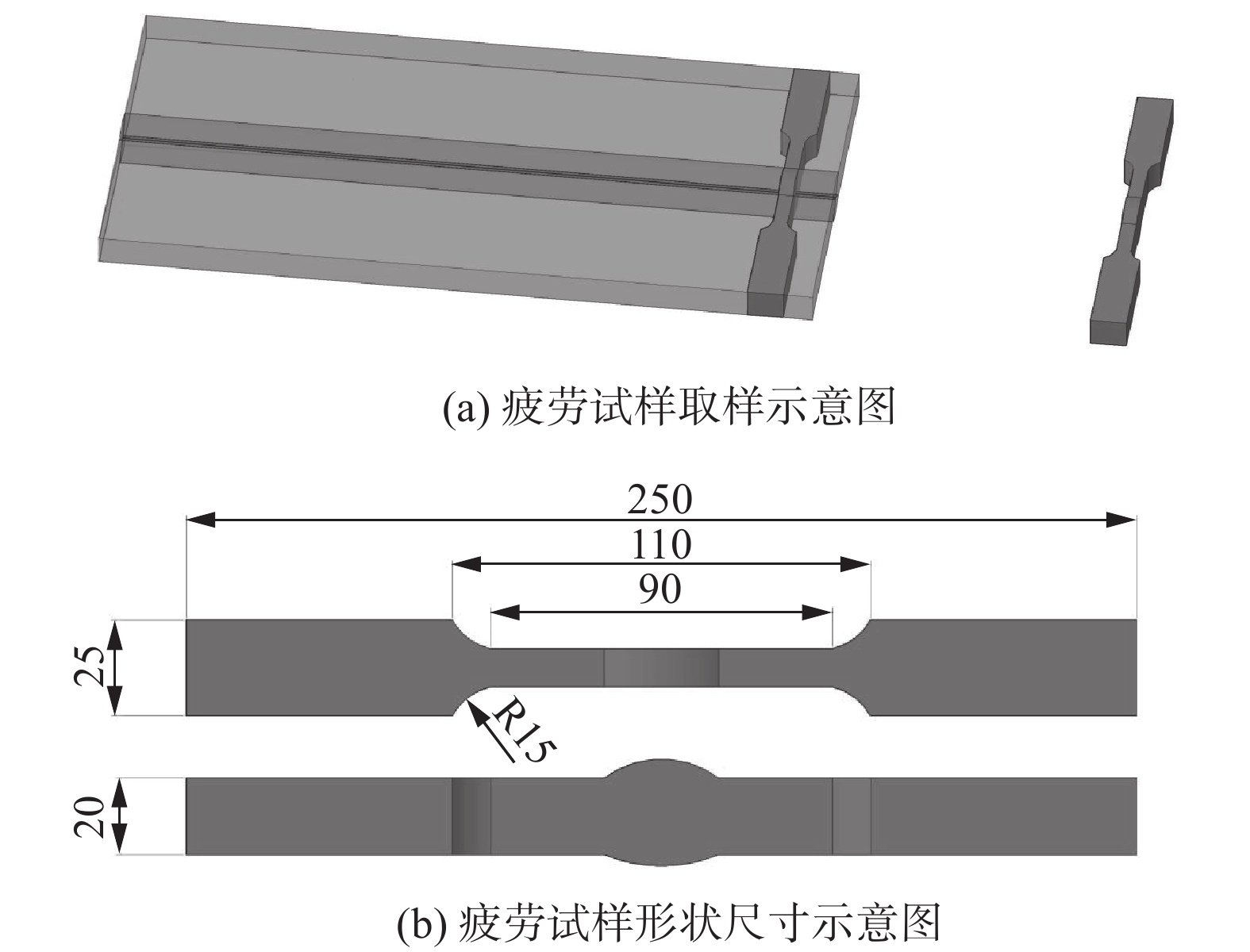
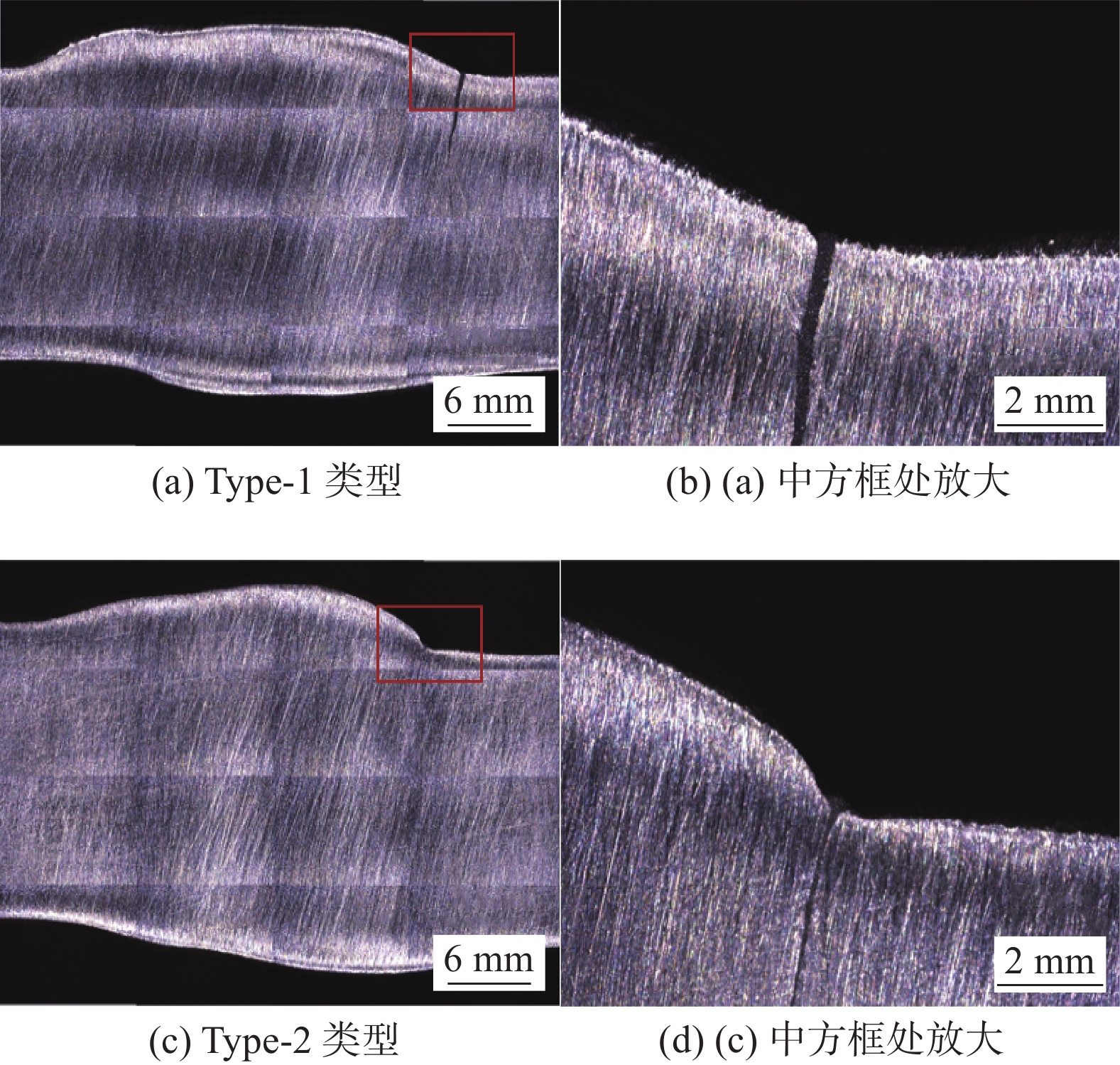
试验材料为船舶结构钢EH36钢，其力学性能见表1. 选取20 mm厚双面全熔透对接焊缝为研究节点[16]，载荷方向垂直于焊缝. 根据ASTM E466-15[17]的标准要求取样，试样形状尺寸如图1所示，采用GMAW打底加SAW填充、盖面的焊接工艺分别制备了Type-1、Type-2两种类型焊缝形貌的焊接接头，如图2a、2c所示. GMAW和SAW关键焊接工艺参数见表2.
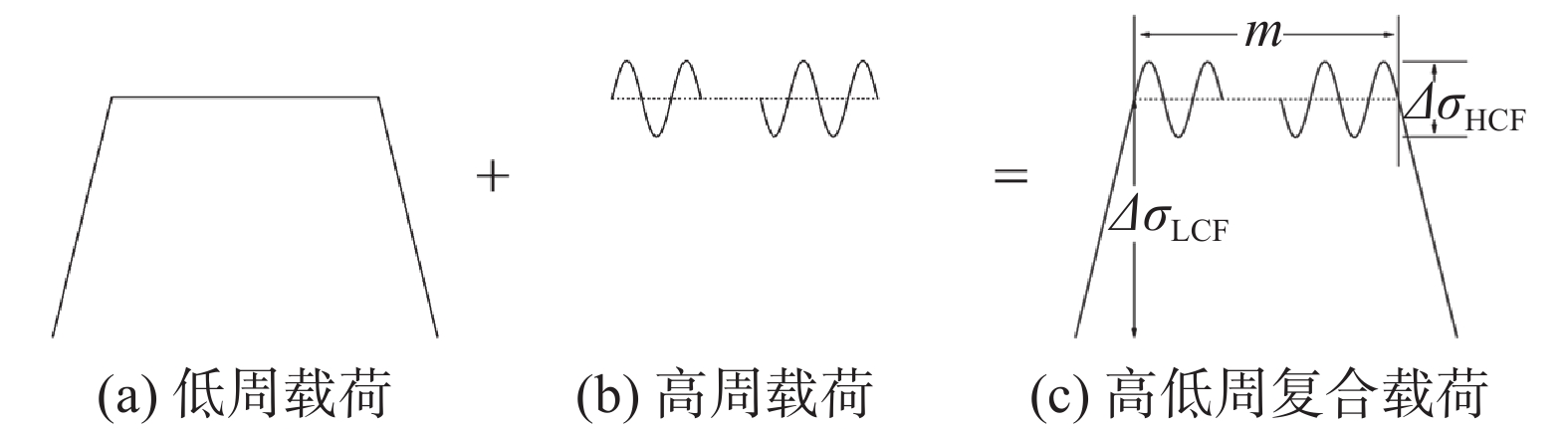
表 1 EH36钢力学性能Table 1. Mechanical properties of EH36 steel牌号 屈服强度ReL/MPa 抗拉强度Rm/MPa 断后伸长率A(%) EH36 ≥355 490 ~ 630 21 ![]()
图 1 疲劳试样取样以及形状尺寸示意图(mm)Figure 1. Sampling, size and form of the fatigue specimens (mm). (a) sampling of the fatigue specimens; (b) size and form of the fatigue specimens![]()
图 2 两种类型试样的焊缝形貌Figure 2. Weld profiles of two specimens. (a) Type-1; (b) magnify of Type-1; (c) Type-2; (d) magnify of Type-2表 2 焊接工艺参数Table 2. Welding process parameters焊接方法 焊丝牌号 电流I/A 焊接速度v/(mm·min−1) GMAW JM-58(ϕ1.2) 127～155 170～280 SAW PREMLER WELD Ni1K(ϕ4.0) 400～650 400～600 疲劳试验分为高低周复合疲劳试验和不同应力比下的常幅疲劳试验. 高低周复合疲劳试验采用的载荷谱由一个低周梯形波载荷(图3a)与叠加在低周载荷峰值上的高周正弦载荷(图3b)组成，如图3c所示. 文中高低周复合疲劳载荷谱中低周载荷应力比RLCF=0.1；高周载荷平均应力σHavg即为低周载荷最大应力σLmax，高周频率为128 Hz，在σHavg=300 MPa，RHCF=0.5、0.6、0.7，三个应力水平下进行试验，高低周复合循环次数比m为10000. 常幅疲劳试验在与高低周复合疲劳载荷相同应力水平的常幅疲劳载荷下进行.
![]()
图 3 疲劳试验载荷示意图Figure 3. Fatigue loadings. (a) low cycle fatigue loading; (b) high cycle fatigue loading; (c) combined high and low fatigue cycle loading为探究焊趾处应力集中对接头疲劳寿命的影响，针对Type-1、Type-2两种类型焊缝形貌的接头试样进行高低周复合疲劳试验和常幅疲劳试验，每个应力水平进行3次重复试验. 两种类型试样在不同应力水平下疲劳失效的位置均发生在焊趾处，如图2b、图2d所示. 用超景深测量两种类型试样断裂位置的焊缝倾角а、板厚T、余高h、焊缝宽度hp、焊趾过渡圆弧半径ρ和错边Δб，见表3.
表 3 两种类型接头焊缝几何参数Table 3. Geometrical parameters of two welded joints试样类型 几何参数 均值 Type-1 焊缝倾角а(°) 26.05 板厚T/mm 20.00 余高h/mm 3.273 焊缝宽度hp/mm 33.74 过渡圆弧半径ρ/mm 8.425 错边Δб/mm 0.937 Type-2 焊缝倾角а(°) 50.60 板厚T/mm 20.00 余高h/mm 4.648 焊缝宽度hp/mm 26.63 过渡圆弧半径ρ/mm 1.022 错边Δб/mm 2.020 2. 试验结果及分析
2.1 EH36钢焊接接头S-N曲线
表4和表5分别为Type-1类型焊接接头在各应力水平下的高低周复合疲劳试验结果和相同应力水平下的常幅疲劳试验结果，表6为R=0.1时的常幅疲劳试验结果.
表 4 Type-1类型接头高低周复合疲劳试验结果Table 4. Combined high and low cycle fatigue test results of Type-1 welded joints试样编号 低周应力比RLCF 高周应力比RHCF 高周应力幅值ΔσHCF/MPa 疲劳寿命N/次 300/0.5C-1 0.1 0.5 200 144983 300/0.5C-2 0.1 0.5 200 126924 300/0.5C-3 0.1 0.5 200 150016 300/0.6C-1 0.1 0.6 150 315563 300/0.6C-2 0.1 0.6 150 327714 300/0.6C-3 0.1 0.6 150 355930 300/0.7C-1 0.1 0.7 106 2010492 300/0.7C-2 0.1 0.7 106 1794010 300/0.7C-3 0.1 0.7 106 1989428 表 5 Type-1类型接头常幅疲劳试验结果(平均应力σavg=300 MPa)Table 5. Constant amplitude fatigue test results of Type-1 welded joints (σavg=300 MPa)试样编号 应力比R 应力幅值Δσ/MPa 疲劳寿命N/次 300/0.5H-1 0.5 200 152302 300/0.5H-2 0.5 200 196278 300/0.5H-3 0.5 200 176452 300/0.6H-1 0.6 150 470065 300/0.6H-2 0.6 150 419282 300/0.6H-3 0.6 150 445682 300/0.7H-1 0.7 106 3099247 300/0.7H-2 0.7 106 2786650 300/0.7H-3 0.7 106 2517640 表 6 Type-1类型接头常幅疲劳试验结果(应力比R=0.1)Table 6. Constant amplitude fatigue test results of Type-1 welded joints(R=0.1)试样编号 应力比R 应力幅值Δσ/MPa 疲劳寿命N/次 300L-1 0.1 270 50291 300L-2 0.1 270 44974 300L-3 0.1 270 40254 222L-1 0.1 200 201218 222L-2 0.1 200 196988 222L-3 0.1 200 151752 166L-1 0.1 150 512587 166L-2 0.1 150 661207 166L-3 0.1 150 470533 高周疲劳载荷叠加在低周疲劳载荷上时，原高周疲劳载荷的平均应力也会相应增大，此时接头的疲劳寿命降低. 比较表5与表6中同一应力幅值的数据，发现接头寿命在平均应力较高时下降，Δσ=200 MPa时下降了4.5%，Δσ=150 MPa时下降了18.81%. 因此，为更直观地比较高低周复合疲劳对焊接接头寿命的影响，可将高低周复合疲劳寿命与其相同应力水平下的常幅疲劳寿命进行比较.
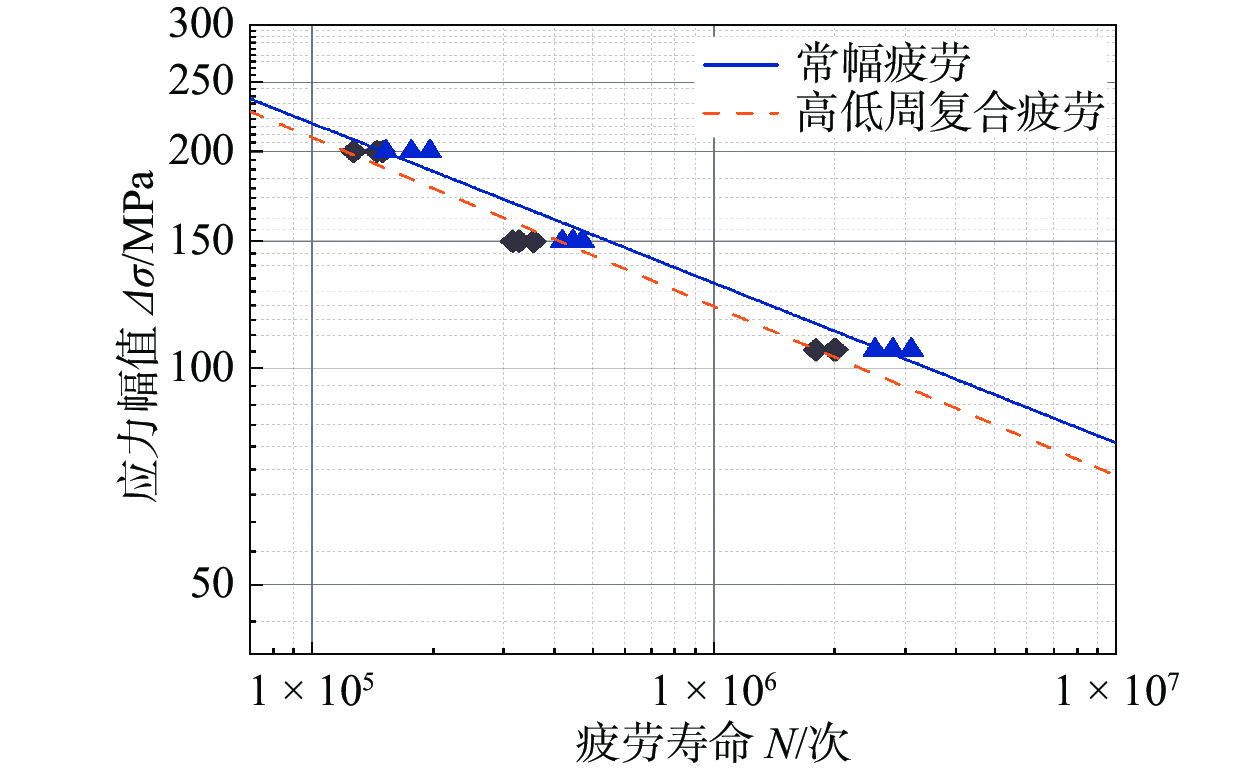
图4为高低周复合疲劳试验S-N曲线与其相同应力水平下常幅疲劳试验S-N曲线. 从图4中可以看出，高低周复合疲劳降低了接头的疲劳寿命，且寿命降低幅度随着高周应力比的增大而增大，具体降低幅度见表7. 当高周应力比为0.5、0.6、0.7时，疲劳寿命分别降低了19.64%、25.15%、30.05%. 其原因是随着复合疲劳中高周应力比的增加，高周应力幅值降低，使得高低周复合疲劳寿命增加，其中低周寿命相应增加，由于低周循环次数的增多，塑性诱导裂纹闭合效应减弱，导致其寿命降低幅度增大[18].
![]()
图 4 Type-1类型接头高低周复合疲劳S-N曲线与常幅疲劳S-N曲线Figure 4. S-N curves of combined high and low cycle fatigue tests and constant amplitude fatigue tests of Type-1 welded joints表 7 不同应力比下高低周复合疲劳寿命降低幅度Table 7. Fatigue life decrease of combined high and low cycle fatigue at different stress ratios应力水平 常幅疲劳寿命
NCAF/次高低周复合疲劳寿命
NCCF/次寿命降低幅度
εN(%)300/0.5 175010 140641 19.64 300/0.6 445009 333069 25.15 300/0.7 2801179 1931310 30.05 2.2 焊趾处应力集中对接头疲劳寿命的影响
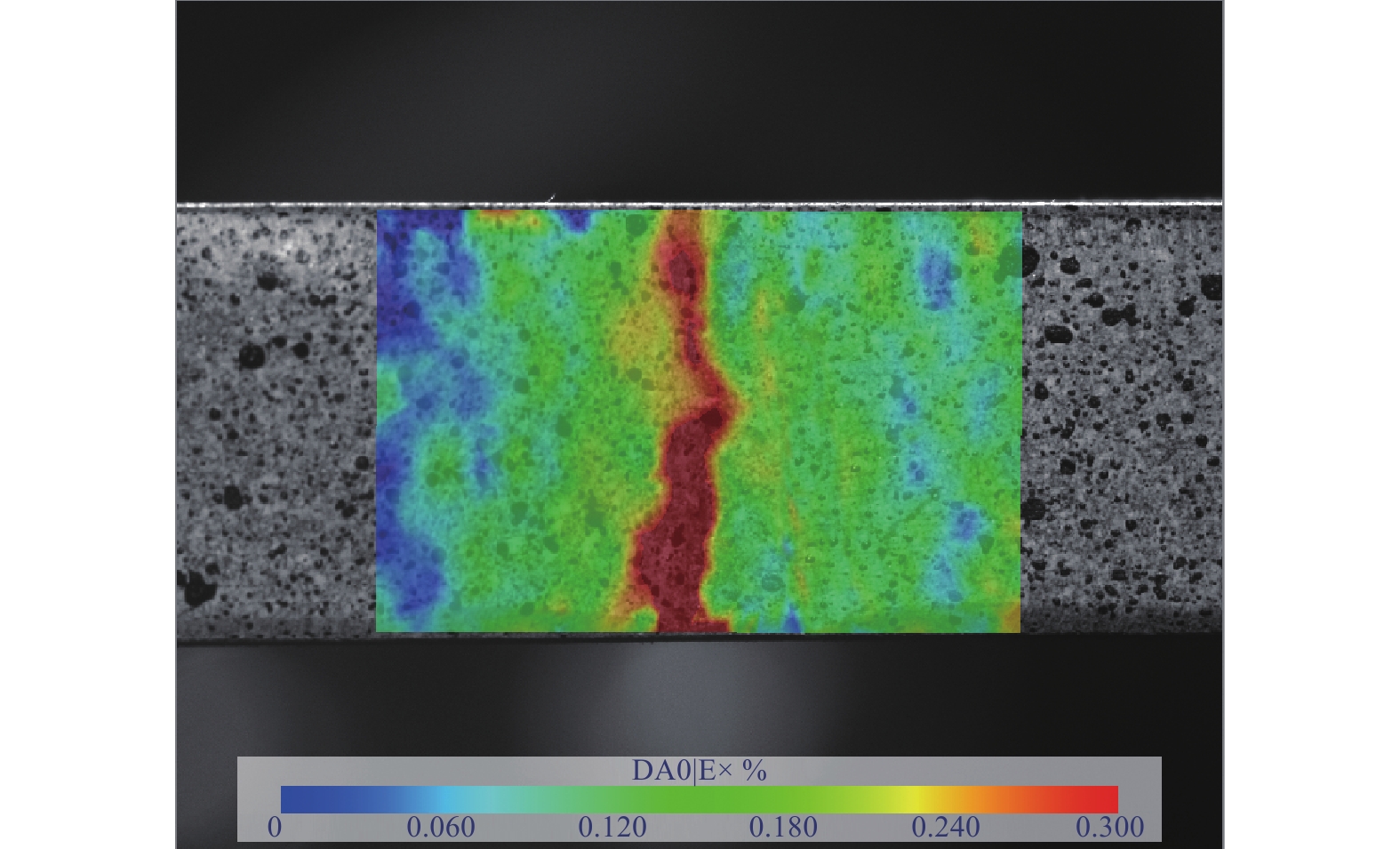
影响焊接接头高低周疲劳寿命的因素除应力水平外，还有焊趾处应力集中. 基于数字图像相关法(digital image correlation method, DIC)测量结果，得到了高低周复合疲劳过程中焊趾处应变场[19]，如图5所示. 从图5可以看出焊趾处应变是周围区域的2倍左右，根据胡克定律中应力应变关系，可从图5推断出焊趾处存在明显应力集中.
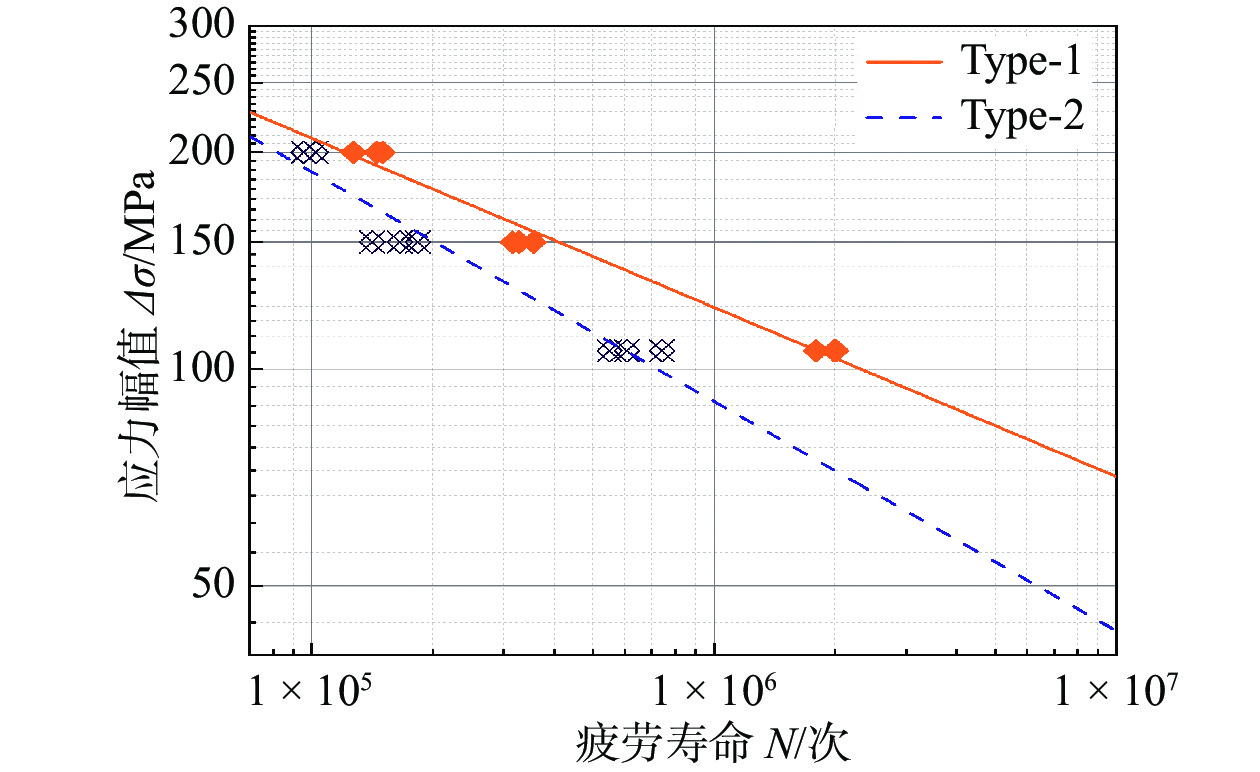
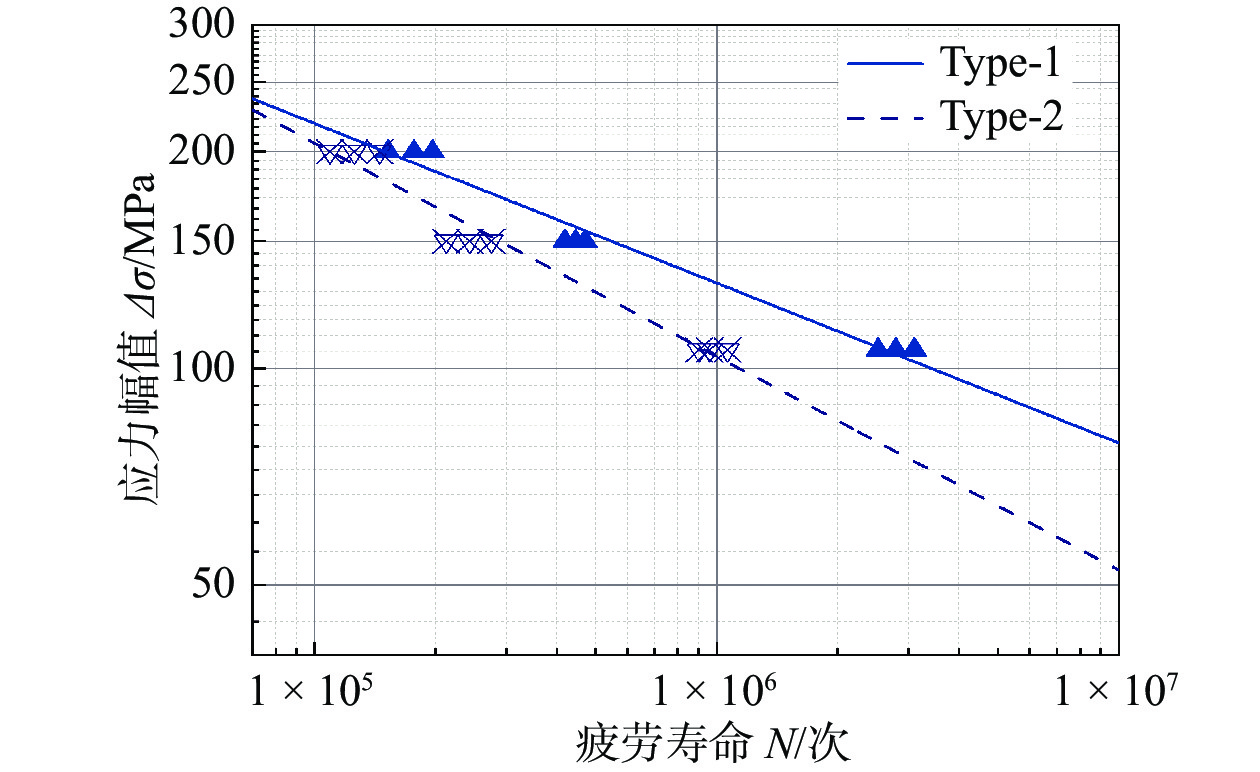
表8和表9分别为Type-2类型焊接接头在各应力水平下的高低周复合疲劳试验结果和相同应力水平下的常幅疲劳试验结果，表10为R=0.1时的常幅疲劳试验结果. 图6、图7分别为Type-1、Type-2两种类型焊缝形貌接头的高低周复合疲劳S-N曲线和对应的常幅疲劳S-N曲线. 从图6、图7可以看出，在相同应力水平下，Type-2类型接头的疲劳寿命较Type-1类型均有降低，具体降低幅度见表11，其降低幅度随着应力比的增大而增大，当应力比为0.5、0.6、0.7，Type-2类型接头的高低周复合疲劳寿命较Type-1类型分别降低了30.59%、50.94%、67.21%.
表 8 Type-2类型接头高低周复合疲劳试验结果Table 8. Combined high and low cycle fatigue test results of Type-2 welded joints试样编号 低周应力比RLCF 高周应力比RHCF 高周应力幅值ΔσHCF/MPa 疲劳寿命N/次 h300/0.5C-1 0.1 0.5 200 95192 h300/0.5C-2 0.1 0.5 200 102212 h300/0.5C-3 0.1 0.5 200 95454 h300/0.6C-1 0.1 0.6 150 141294 h300/0.6C-2 0.1 0.6 150 165487 h300/0.6C-3 0.1 0.6 150 183425 h300/0.7C-1 0.1 0.7 106 550027 h300/0.7C-2 0.1 0.7 106 742598 h300/0.7C-3 0.1 0.7 106 607245 表 9 Type-2类型接头常幅疲劳试验结果(平均应力σavg=300 MPa)Table 9. Constant amplitude fatigue test results of Type-2 welded joints(σavg=300 MPa)试样编号 应力比R 应力幅值Δσ/MPa 疲劳寿命N/次 h300/0.5H-1 0.5 200 125423 h300/0.5H-2 0.5 200 145009 h300/0.5H-3 0.5 200 109157 h300/0.6H-1 0.6 150 212545 h300/0.6H-2 0.6 150 274904 h300/0.6H-3 0.6 150 242758 h300/0.7H-1 0.7 106 902564 h300/0.7H-2 0.7 106 1062651 h300/0.7H-3 0.7 106 959898 表 10 Type-2类型接头常幅疲劳试验结果(应力比R=0.1)Table 10. Constant amplitude fatigue test results of Type-2 welded joints (R=0.1)试样编号 应力比R 应力幅值Δσ/MPa 疲劳寿命N/次 h300L-1 0.1 297 25145 h300L-2 0.1 297 30026 h300L-3 0.1 297 25229 ![]()
图 6 两种类型焊缝形貌焊接接头高低周复合疲劳S-N曲线Figure 6. S-N curves of combined high and low cycle fatigue tests of welded joints with two weld profiles![]()
图 7 两种类型焊缝形貌焊接接头常幅疲劳S-N曲线Figure 7. S-N curves of high cycle fatigue tests of welded joints with two weld profiles$$\begin{split} K_t=&1 + \dfrac{1-e^{\left(-0.9a \sqrt{\dfrac{T + 2 h + 0.6 h_o}{2 h}}\right)}}{1-e^{\left(-0.45 t \text{π} \sqrt{\dfrac{T + 2 h + 0.6 h_o}{2 h}}\right)}} \times 2 \\&\times \left[\dfrac{h}{\rho} \cdot \dfrac{1}{2.8 \times\left(\dfrac{T + 2 h + 0.6 \cdot h_p}{T}\right)-2}\right]^{0.65} \end{split} $$ (1) 经计算，Type-1类型接头焊趾处应力集中系数为1.414，Type-2类型接头焊趾处应力集中系数为3.603.
表 11 焊接接头寿命降低幅度Table 11. Fatigue life decrease of welded joints应力水平 Type-1类型接头
疲劳寿命N1/次Type-2类型接头
疲劳寿命N2/次寿命降低幅度
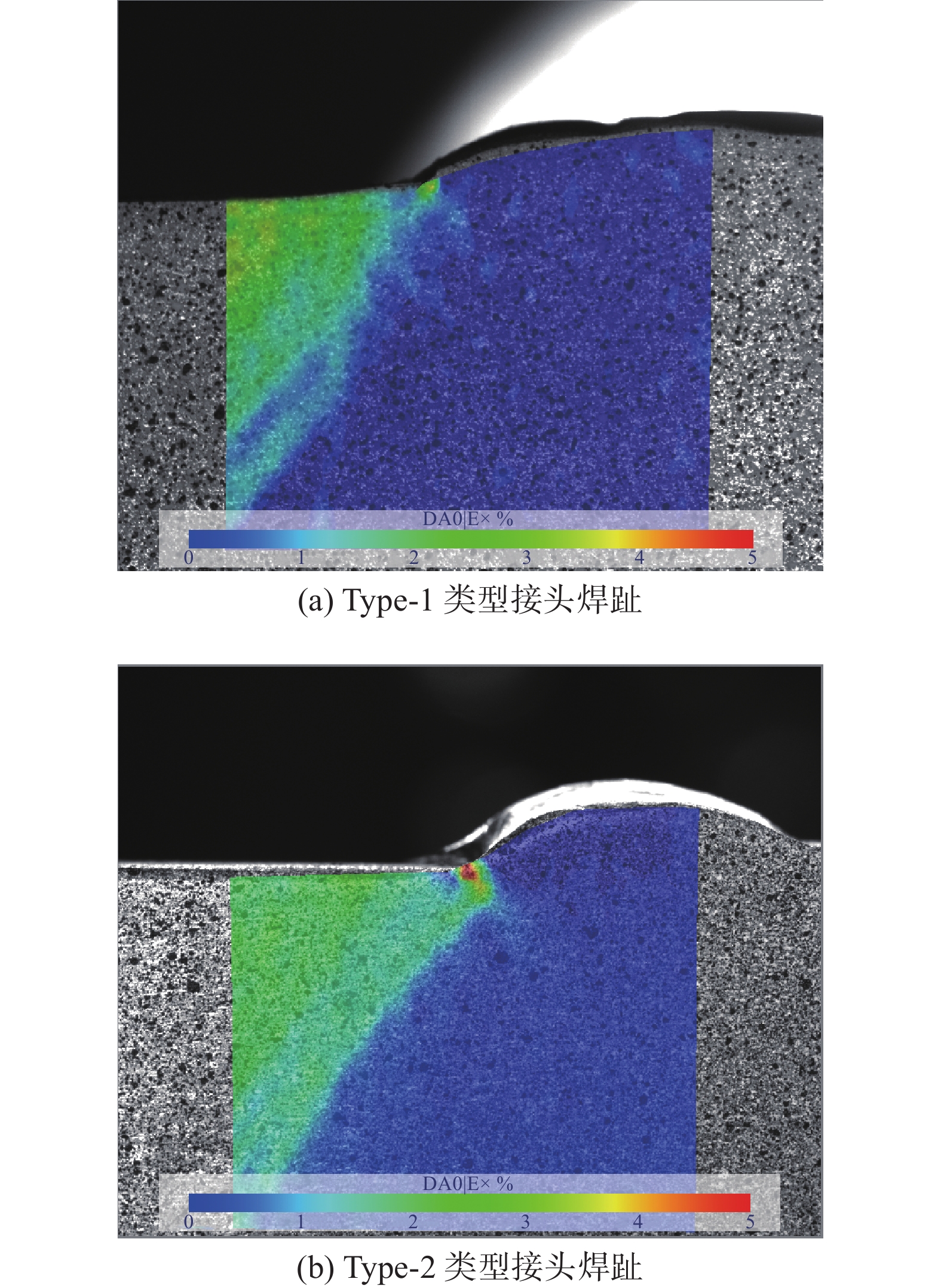
εN(%)300/0.5C 140641 97619 30.59 300/0.6C 333069 163402 50.94 300/0.7C 1931310 646312 67.21 300/0.5H 175010 126529 27.70 300/0.6H 445009 243402 45.30 300/0.7H 2801179 975037 65.19 300L 45173 28304 37.34 图8为同一寿命下两种类型接头焊趾处应变场，Type-2类型接头焊趾处应变约是Type-1类型接头的2.5倍，根据胡克定律中应力应变关系，可推断出Type-2类型接头焊趾处应力集中较Type-1类型接头更为明显，这与应力集中系数Kt有很好的对应关系，焊缝几何不连续性越大，焊趾处应力集中越大，接头疲劳寿命越低[11, 22]. 试验采用的试样加工时基本释放了焊接残余应力[23]，若焊接结构中存在残余应力，可修正平均应力来考虑残余应力的影响[24].
![]()
图 8 两种类型接头焊趾处应力集中Figure 8. Strain fields at weld toes of two weld profiles. (a) strain fields at weld toe of Type-1 welded joint; (b) strain fields at weld toe of Type-2 welded joint2.3 高低周复合疲劳寿命预测
变幅载荷下疲劳寿命预测常用Palmgren-Miner线性模型，但实际上高低周复合疲劳寿命NCCF不只是低周寿命NLCF与高周寿命NHCF的简单线性叠加，二者之间存在着交互作用. 忽略高低周疲劳载荷的交互作用将导致试样疲劳寿命被高估，不能保证结构安全性的要求[25-27]. 此外，焊趾处应力集中也很大程度影响着高低周复合疲劳寿命预测模型的精确性.
为研究高低周复合模型对EH36钢焊接接头疲劳寿命预测的适用性，对Palmgren-Miner模型[28]、T-K模型[29]和Zhu模型[30]进行验证，模型中材料常数根据试验数据拟合[31].
Palmgren-Miner模型：
$$ {N_{\text{CCF}}} = \dfrac{{1 + m}}{{\dfrac{m}{{{N_{{\text{HCF}}}}}} + \dfrac{1}{{{N_{{\text{LCF}}}}}}}} $$ (2) 式中：NCCF为高低周复合疲劳寿命；NHCF为高周寿命；NLCF为低周寿命；m为高低周复合循环次数比.
T-K模型：
$$ {N_{\text{CCF}}} = \left( {1 + m} \right) \cdot {N_{{\text{LCF}}}} \cdot {\left( {\dfrac{1}{m}} \right)^{\gamma \cdot \alpha }} $$ (3) 式中：NCCF为高低周复合疲劳寿命；NLCF为低周寿命；m为高低周复合循环次数比；γ为材料常数，取1.55；α为高低周应力幅值比.
Zhu模型：
$$ {N_{{\text{CCF}}}} = \dfrac{{1 + m}}{{\dfrac{m}{{{N_{{\text{HCF}}}}}} + \dfrac{1}{{{N_{{\text{LCF}}}}}} + \dfrac{1}{{\left( {m + 1} \right) \cdot \lg {{\left( {{N_{{\text{HCF}}}}} \right)}^\alpha }}}}} $$ (4) 式中：NCCF为高低周复合疲劳寿命；NHCF为高周寿命；NLCF为低周寿命；m为高低周复合循环次数比；α为高低周应力幅值比.
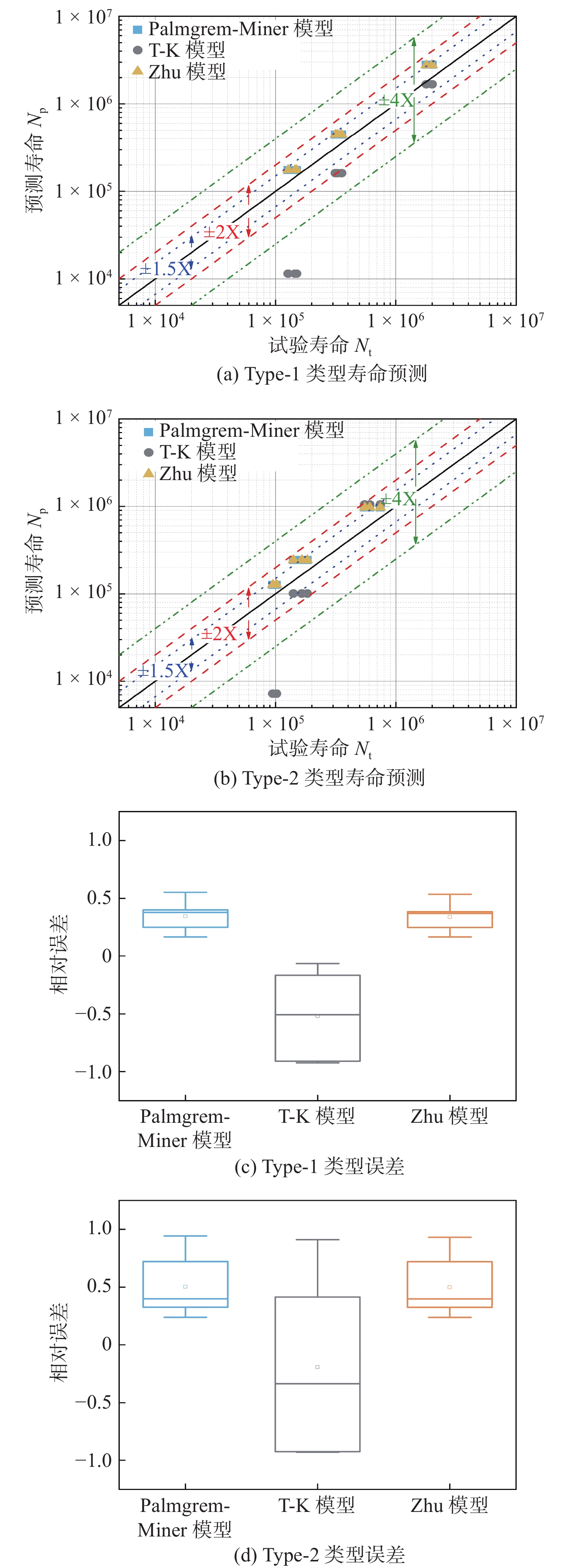
基于试样试验寿命Nt和模型预测寿命Np绘制两种类型接头的高低周复合疲劳寿命预测图和误差箱线图，如图9所示. 寿命预测图中的点线、划线和双点划线分别表示1.5倍分散带、2倍分散带和4倍分散带. 从图9中可以看出，应力集中系数大的焊接接头高低周复合疲劳寿命预测结果分散性大，可能原因是焊趾处应力集中对高低周耦合损伤有一定影响.
![]()
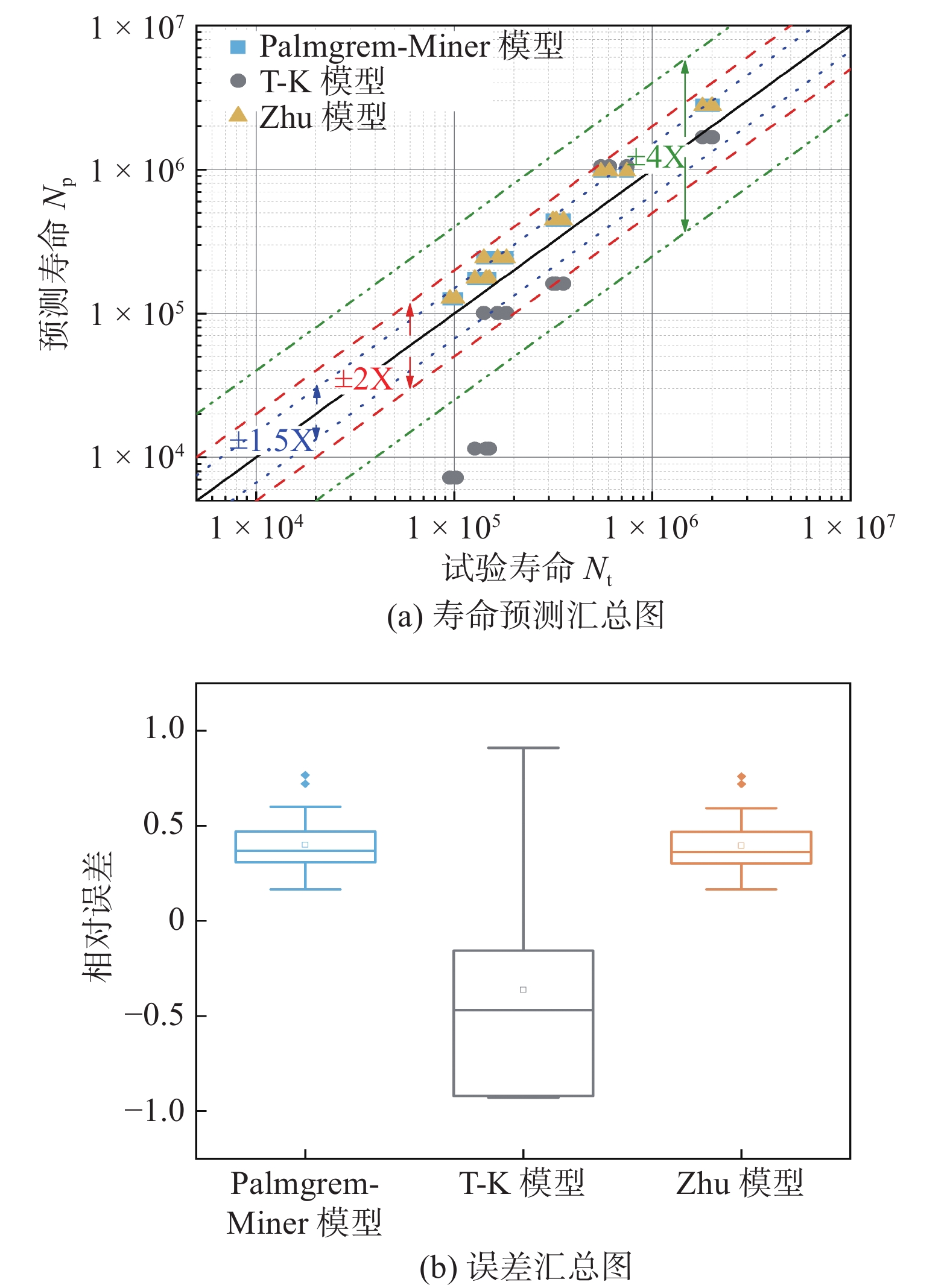
图 9 两种类型焊接接头寿命预测图和误差箱线图Figure 9. Life prediction and error under two weld profiles. (a) Life prediction under Type-1 welded joints; (b) Life prediction under Type-2 welded joints; (c) error under Type-1 welded joints; (d) error under Type-2 welded joints图10为寿命预测汇总图和误差箱线汇总图，从图10中可以看出，Palmgren-Miner模型的高低周复合疲劳寿命预测结果相对实际寿命偏大，预测结果相对危险. T-K模型的预测寿命分散性较大，误差也较大，出现了在4倍寿命分散带以外的预测点，该模型不适用于EH36钢焊接接头高低周复合疲劳寿命预测. 由于试验中高低周复合疲劳循环次数比m较大，Zhu模型在考虑高低周复合疲劳耦合损伤作用后，其寿命预测结果与Palmgren-Miner模型相比仍没有明显差异.
![]()
图 10 寿命预测汇总图和误差箱线汇总图Figure 10. Summary of life prediction and error. (a) summary of life prediction; (b) summary of error通过分析发现，Zhu模型考虑了一个循环内m次高周疲劳循环和1次低周疲劳循环的交互作用，对于高低周复合循环次数比m大的情况，Zhu模型会高估m对耦合作用的影响，模型应用受到限制[32]. 因此根据实际情况，将高低周复合疲劳过程中由高周平均应力卸载到低周最低应力，再次加载到高周平均应力这一过程视为高低周复合疲劳的1次交互作用，并对Zhu模型进行修正，将耦合损伤项修正为1/log(NHCF)α.
得到修正后的Zhu模型，即
$$ {N_{{\text{CCF}}}} = \dfrac{{1 + m}}{{\dfrac{m}{{{N_{{\text{HCF}}}}}} + \dfrac{1}{{{N_{{\text{LCF}}}}}} + \dfrac{1}{{\lg {{({N_{{\text{HCF}}}})}^\alpha }}}}} $$ (5) 图11为Zhu模型修正前后的寿命预测图和误差箱线图. 从图11中可以看出，修正后Zhu模型的高低周复合疲劳寿命预测结果分散性较小，误差也较小，预测点均处于1.5倍分散带以内，且预测寿命大于实际寿命的预测点较少，寿命预测结果相对安全.
![]()
图 11 修改前后Zhu模型寿命预测图和误差箱线图Figure 11. Life prediction and error of Zhu model. (a) life prediction of Zhu model; (b) error of Zhu model3. 结论
(1)高低周复合疲劳对寿命的影响随着高周应力比的增大而增大. 相同应力幅值下，接头寿命随平均应力增大而降低.
(2)在相同载荷条件下，焊趾处应力集中系数越大，接头的高低周复合疲劳寿命越低，其寿命降低幅值随着高周应力比的增大而增大. 此外，焊趾处应力集中系数大的接头寿命预测结果分散性大.
(3)Palmgren-Miner模型和Zhu模型寿命预测结果相对危险. 修正后Zhu模型的寿命预测结果分散性较小，误差也较小，预测结果相对安全.
-
![]()
图 1 疲劳试样取样以及形状尺寸示意图(mm)
Figure 1. Sampling, size and form of the fatigue specimens (mm). (a) sampling of the fatigue specimens; (b) size and form of the fatigue specimens
![]()
图 2 两种类型试样的焊缝形貌
Figure 2. Weld profiles of two specimens. (a) Type-1; (b) magnify of Type-1; (c) Type-2; (d) magnify of Type-2
![]()
图 3 疲劳试验载荷示意图
Figure 3. Fatigue loadings. (a) low cycle fatigue loading; (b) high cycle fatigue loading; (c) combined high and low fatigue cycle loading
![]()
图 4 Type-1类型接头高低周复合疲劳S-N曲线与常幅疲劳S-N曲线
Figure 4. S-N curves of combined high and low cycle fatigue tests and constant amplitude fatigue tests of Type-1 welded joints
![]()
图 6 两种类型焊缝形貌焊接接头高低周复合疲劳S-N曲线
Figure 6. S-N curves of combined high and low cycle fatigue tests of welded joints with two weld profiles
![]()
图 7 两种类型焊缝形貌焊接接头常幅疲劳S-N曲线
Figure 7. S-N curves of high cycle fatigue tests of welded joints with two weld profiles
![]()
图 8 两种类型接头焊趾处应力集中
Figure 8. Strain fields at weld toes of two weld profiles. (a) strain fields at weld toe of Type-1 welded joint; (b) strain fields at weld toe of Type-2 welded joint
![]()
图 9 两种类型焊接接头寿命预测图和误差箱线图
Figure 9. Life prediction and error under two weld profiles. (a) Life prediction under Type-1 welded joints; (b) Life prediction under Type-2 welded joints; (c) error under Type-1 welded joints; (d) error under Type-2 welded joints
![]()
图 10 寿命预测汇总图和误差箱线汇总图
Figure 10. Summary of life prediction and error. (a) summary of life prediction; (b) summary of error
![]()
图 11 修改前后Zhu模型寿命预测图和误差箱线图
Figure 11. Life prediction and error of Zhu model. (a) life prediction of Zhu model; (b) error of Zhu model
表 1 EH36钢力学性能
Table 1 Mechanical properties of EH36 steel
牌号 屈服强度ReL/MPa 抗拉强度Rm/MPa 断后伸长率A(%) EH36 ≥355 490 ~ 630 21 
下载: 导出CSV
表 2 焊接工艺参数
Table 2 Welding process parameters
焊接方法 焊丝牌号 电流I/A 焊接速度v/(mm·min−1) GMAW JM-58(ϕ1.2) 127～155 170～280 SAW PREMLER WELD Ni1K(ϕ4.0) 400～650 400～600
下载: 导出CSV
表 3 两种类型接头焊缝几何参数
Table 3 Geometrical parameters of two welded joints
试样类型 几何参数 均值 Type-1 焊缝倾角а(°) 26.05 板厚T/mm 20.00 余高h/mm 3.273 焊缝宽度hp/mm 33.74 过渡圆弧半径ρ/mm 8.425 错边Δб/mm 0.937 Type-2 焊缝倾角а(°) 50.60 板厚T/mm 20.00 余高h/mm 4.648 焊缝宽度hp/mm 26.63 过渡圆弧半径ρ/mm 1.022 错边Δб/mm 2.020
下载: 导出CSV
表 4 Type-1类型接头高低周复合疲劳试验结果
Table 4 Combined high and low cycle fatigue test results of Type-1 welded joints
试样编号 低周应力比RLCF 高周应力比RHCF 高周应力幅值ΔσHCF/MPa 疲劳寿命N/次 300/0.5C-1 0.1 0.5 200 144983 300/0.5C-2 0.1 0.5 200 126924 300/0.5C-3 0.1 0.5 200 150016 300/0.6C-1 0.1 0.6 150 315563 300/0.6C-2 0.1 0.6 150 327714 300/0.6C-3 0.1 0.6 150 355930 300/0.7C-1 0.1 0.7 106 2010492 300/0.7C-2 0.1 0.7 106 1794010 300/0.7C-3 0.1 0.7 106 1989428
下载: 导出CSV
表 5 Type-1类型接头常幅疲劳试验结果(平均应力σavg=300 MPa)
Table 5 Constant amplitude fatigue test results of Type-1 welded joints (σavg=300 MPa)
试样编号 应力比R 应力幅值Δσ/MPa 疲劳寿命N/次 300/0.5H-1 0.5 200 152302 300/0.5H-2 0.5 200 196278 300/0.5H-3 0.5 200 176452 300/0.6H-1 0.6 150 470065 300/0.6H-2 0.6 150 419282 300/0.6H-3 0.6 150 445682 300/0.7H-1 0.7 106 3099247 300/0.7H-2 0.7 106 2786650 300/0.7H-3 0.7 106 2517640
下载: 导出CSV
表 6 Type-1类型接头常幅疲劳试验结果(应力比R=0.1)
Table 6 Constant amplitude fatigue test results of Type-1 welded joints(R=0.1)
试样编号 应力比R 应力幅值Δσ/MPa 疲劳寿命N/次 300L-1 0.1 270 50291 300L-2 0.1 270 44974 300L-3 0.1 270 40254 222L-1 0.1 200 201218 222L-2 0.1 200 196988 222L-3 0.1 200 151752 166L-1 0.1 150 512587 166L-2 0.1 150 661207 166L-3 0.1 150 470533
下载: 导出CSV
表 7 不同应力比下高低周复合疲劳寿命降低幅度
Table 7 Fatigue life decrease of combined high and low cycle fatigue at different stress ratios
应力水平 常幅疲劳寿命
NCAF/次高低周复合疲劳寿命
NCCF/次寿命降低幅度
εN(%)300/0.5 175010 140641 19.64 300/0.6 445009 333069 25.15 300/0.7 2801179 1931310 30.05
下载: 导出CSV
表 8 Type-2类型接头高低周复合疲劳试验结果
Table 8 Combined high and low cycle fatigue test results of Type-2 welded joints
试样编号 低周应力比RLCF 高周应力比RHCF 高周应力幅值ΔσHCF/MPa 疲劳寿命N/次 h300/0.5C-1 0.1 0.5 200 95192 h300/0.5C-2 0.1 0.5 200 102212 h300/0.5C-3 0.1 0.5 200 95454 h300/0.6C-1 0.1 0.6 150 141294 h300/0.6C-2 0.1 0.6 150 165487 h300/0.6C-3 0.1 0.6 150 183425 h300/0.7C-1 0.1 0.7 106 550027 h300/0.7C-2 0.1 0.7 106 742598 h300/0.7C-3 0.1 0.7 106 607245
下载: 导出CSV
表 9 Type-2类型接头常幅疲劳试验结果(平均应力σavg=300 MPa)
Table 9 Constant amplitude fatigue test results of Type-2 welded joints(σavg=300 MPa)
试样编号 应力比R 应力幅值Δσ/MPa 疲劳寿命N/次 h300/0.5H-1 0.5 200 125423 h300/0.5H-2 0.5 200 145009 h300/0.5H-3 0.5 200 109157 h300/0.6H-1 0.6 150 212545 h300/0.6H-2 0.6 150 274904 h300/0.6H-3 0.6 150 242758 h300/0.7H-1 0.7 106 902564 h300/0.7H-2 0.7 106 1062651 h300/0.7H-3 0.7 106 959898
下载: 导出CSV
表 10 Type-2类型接头常幅疲劳试验结果(应力比R=0.1)
Table 10 Constant amplitude fatigue test results of Type-2 welded joints (R=0.1)
试样编号 应力比R 应力幅值Δσ/MPa 疲劳寿命N/次 h300L-1 0.1 297 25145 h300L-2 0.1 297 30026 h300L-3 0.1 297 25229
下载: 导出CSV
表 11 焊接接头寿命降低幅度
Table 11 Fatigue life decrease of welded joints
应力水平 Type-1类型接头
疲劳寿命N1/次Type-2类型接头
疲劳寿命N2/次寿命降低幅度
εN(%)300/0.5C 140641 97619 30.59 300/0.6C 333069 163402 50.94 300/0.7C 1931310 646312 67.21 300/0.5H 175010 126529 27.70 300/0.6H 445009 243402 45.30 300/0.7H 2801179 975037 65.19 300L 45173 28304 37.34
下载: 导出CSV
-
[1] Wang Y, Liu J, Hu J, et al. Fatigue strength of EH36 steel welded joints and base material at low-temperature[J]. International Journal of Fatigue, 2021, 142: 105896. doi: 10.1016/j.ijfatigue.2020.105896
[2] Song Y, Yang P, Xia T, et al. The crack growth rate and crack opening displacement of EH-36 steel under low-cycle fatigue loading[J]. Ocean Engineering, 2023, 280: 114734. doi: 10.1016/j.oceaneng.2023.114734
[3] Li L, Jia Q, Wan Z, et al. Experimental and numerical investigation of effects of residual stress and its release on fatigue strength of typical FPSO-unit welded joint[J]. Ocean Engineering, 2020, 196: 106858. doi: 10.1016/j.oceaneng.2019.106858
[4] Wang C, Wang S, Xie L, et al. Fatigue crack growth behavior of marine steel under variable amplitude loading-combining DIC technique and SEM observation[J]. International Journal of Fatigue, 2023, 170: 107508. doi: 10.1016/j.ijfatigue.2023.107508
[5] Ibarra M A C, Simão M L, Videiro P M, et al. Long-term fatigue analysis of mooring lines considering wind-sea and swell waves using the Univariate Dimension-Reduction Method[J]. Applied Ocean Research, 2022, 118: 102997. doi: 10.1016/j.apor.2021.102997
[6] 魏国前, 陈斯雯, 余茜, 等. 焊趾多裂纹的试验与仿真分析[J]. 焊接学报, 2019, 40(11): 75 − 81. doi: 10.12073/j.hjxb.2019400291 Wei Guoqian, Chen Siwen, Yu Xi, et al. Experimental and simulation study on multiple cracks of weld toe[J]. Transactions of the China Welding Institution, 2019, 40(11): 75 − 81. doi: 10.12073/j.hjxb.2019400291
[7] Luo Y, Ma R, Tsutsumi S. Parametric formulae for elastic stress concentration factor at the weld toe of distorted butt-welded joints[J]. Materials, 2020, 13(1): 169. doi: 10.3390/ma13010169
[8] Ottersböck M J, Leitner M, Stoschka M. Characterisation of actual weld geometry and stress concentration of butt welds exhibiting local undercuts[J]. Engineering Structures, 2021, 240: 112266. doi: 10.1016/j.engstruct.2021.112266
[9] 张晨星. 焊缝形貌对焊接强度的影响研究[D]. 河北: 燕山大学. 2022. Zhang Chenxing. Study on the influence of weld morphology on weld strength[D]. Yanshan: Yanshan University. 2022.
[10] Wu X, Kang H. A fracture mechanics-based stress approach for fatigue life prediction of welded joints considering weld profile effect[J]. Theoretical and Applied Fracture Mechanics, 2023, 123: 103698. doi: 10.1016/j.tafmec.2022.103698
[11] Bai S, Li Y, Huang H, et al. A probabilistic combined high and low cycle fatigue life prediction framework for the turbine shaft with random geometric parameters[J]. International Journal of Fatigue, 2022, 165: 107218. doi: 10.1016/j.ijfatigue.2022.107218
[12] Tsutsumi S, Fincato R, Luo P, et al. Effects of weld geometry and HAZ property on low-cycle fatigue behavior of welded joint[J]. International Journal of Fatigue, 2022, 156: 106683. doi: 10.1016/j.ijfatigue.2021.106683
[13] Gan J, Liu X, Wang Z, et al. Experimental study on the fatigue damage of designed T-type specimen with high-low frequency superimposed loading[J]. International Journal of Fatigue, 2021, 143: 105985. doi: 10.1016/j.ijfatigue.2020.105985
[14] Qiu S, Cui H, Zhang H, et al. A dual-threshold modelling approach for fatigue life prediction under combined high and low cycle fatigue[J]. International Journal of Fatigue, 2022, 164: 107110. doi: 10.1016/j.ijfatigue.2022.107110
[15] Zhao Z, Lu K, Wang L, et al. Prediction of combined cycle fatigue life of TC11 alloy based on modified nonlinear cumulative damage model[J]. Chinese Journal of Aeronautics, 2021, 34(7): 73 − 84. doi: 10.1016/j.cja.2020.10.021
[16] Det Norske Veritas. Fatigue strength analysis of offshore steel structures[S]. Norway: Academic Press, 2001.
[17] ASTM E466-Standard practice for conducting force controlled constant amplitude axial fatigue tests of metallic materials[S]. England: Edinburgh University Press, 2015.
[18] Liang H, Zhan R, Wang D, et al. Effect of crack-tip deformation on fatigue crack growth: A comparative study under overload/underload conditions[J]. Theoretical and Applied Fracture Mechanics, 2022, 118: 103268. doi: 10.1016/j.tafmec.2022.103268
[19] Huang H, Hu M, Xu A, et al. In-situ strain measurement and error analysis of arc welding with 2D digital image correlation[J]. China Welding, 2022, 31(3): 17 − 23.
[20] Ushirokawa O. Stress concentration factor at welded joints. II.-probabilistic approach[J]. Ishikawajima-Harima Engineering Review, 1984, 24(2): 98 − 103.
[21] Tsuji I. Estimation of stress concentration factor at weld toe of non-load carrying fillet welded joints[J]. Journal of the West-Japan Society of Naval Architects, 1990, 80: 241 − 251.
[22] 徐连勇, 彭晨涛, 赵雷, 等. 深水浮体平台焊接结构疲劳性能测试方法[J]. 焊接学报, 2022, 43(11): 84 − 90. doi: 10.12073/j.hjxb.20220703001 Xu Lianyong, Peng Chentao, Zhao Lei, et al. Research on fatigue performance test method of welding structure of floating platform in deep water[J]. Transactions of the China Welding Institution, 2022, 43(11): 84 − 90. doi: 10.12073/j.hjxb.20220703001
[23] 周昊, 刘英芳, 刘刚, 等. 考虑残余应力的焊接结构多轴疲劳准则[J]. 焊接学报, 2017, 38(11): 41 − 46. doi: 10.12073/j.hjxb.20160114002 Zhou Hao, Liu Yingfang, Liu Gang, et al. Multiaxial fatigue criteria of welded structures considering the residual stress[J]. Transactions of the China Welding Institution, 2017, 38(11): 41 − 46. doi: 10.12073/j.hjxb.20160114002
[24] Jiang W, Xie X, Wang T, et al. Fatigue life prediction of 316L stainless steel weld joint including the role of residual stress and its evolution: Experimental and modelling[J]. International Journal of Fatigue, 2021, 143: 105997. doi: 10.1016/j.ijfatigue.2020.105997
[25] 张涛, 王东坡, 邓彩艳, 等. 双周疲劳载荷作用下焊接接头线性累计损伤分析[J]. 焊接学报, 2014, 35(3): 61 − 65. Zhang Tao, Wang Dongpo, Deng Caiyan, et al. Linear cumulative damage analysis of welded joints under combined cycle fatigue[J]. Transactions of the China Welding Institution, 2014, 35(3): 61 − 65.
[26] 幸杰, 韩永典, 徐连勇, 等. 基于连续损伤力学的高低周复合疲劳损伤[J]. 焊接学报, 2017, 38(7): 63 − 66. doi: 10.12073/j.hjxb.20150708001 Xing Jie, Han Yongdian, Xu Lianyong, et al. High cycle and low cycle hybrid fatigue damage based on continuum damage mechanics[J]. Transactions of the China Welding Institution, 2017, 38(7): 63 − 66. doi: 10.12073/j.hjxb.20150708001
[27] 魏国前, 郭子贤, 闫梦煜, 等. 基于Pavlou方法的焊接结构疲劳寿命预测[J]. 焊接学报, 2023, 44(9): 16 − 23. doi: 10.12073/j.hjxb.20221201001 Wei Guoqian, Guo Zixian, Yan Mengyu, et al. Pavlou approach based fatigue life prediction for welded structures[J]. Transactions of the China Welding Institution, 2023, 44(9): 16 − 23. doi: 10.12073/j.hjxb.20221201001
[28] Miner M A. Cumulative damage in fatigue[J]. Journal of Applied Mechanics, 1945, 12: 159 − 164. doi: 10.1115/1.4009458
[29] Trufyakov V I, Koval' chuk V S. Determination of life under two-frequency loading. Report no. 2. Proposed method[J]. Strength of Materials, 1982, 14(10): 1303 − 1308. doi: 10.1007/BF00770123
[30] Zhu S, Yue P, Yu Z, et al. A Combined high and low cycle fatigue model for life prediction of turbine blades[J]. Materials, 2017, 10(7): 698. doi: 10.3390/ma10070698
[31] Han L, Huang D, Yan X, et al. Combined high and low cycle fatigue life prediction model based on damage mechanics and its application in determining the aluminized location of turbine blade[J]. International Journal of Fatigue, 2019, 127: 120 − 130. doi: 10.1016/j.ijfatigue.2019.05.022
[32] 杨民, 李青键, 黄志勇. 低周-超高周复合循环疲劳实验及寿命模型研究[J]. 实验力学, 2021, 36(5): 638 − 646. doi: 10.7520/1001-4888-20-175 Yang Min, Li Qingjian, Huang Zhiyong. Combined low and very-high cycle fatigue test and life model study[J]. Journal of Experimental Mechanics, 2021, 36(5): 638 − 646. doi: 10.7520/1001-4888-20-175
计量
- 文章访问数: 168
- HTML全文浏览量: 18
- PDF下载量: 50
