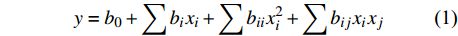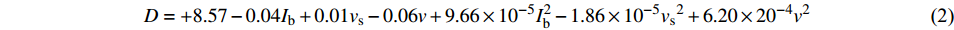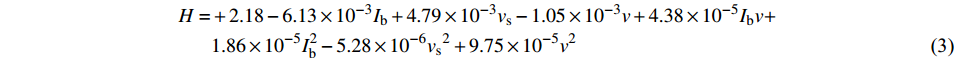-
摘要: 采用响应面法对超高频电弧增材制造工艺（UHFP-GTAW）进行了优化. 通过建立函数关系得到了焊缝尺寸关于焊接电流、送丝速度及焊接速度的多元二次回归模型，并运用方差分析验证了回归模型的可靠性. 设置优化条件选取了相应的焊接参数，并将焊缝尺寸的预测结果与试验结果进行了对比.结果表明，模型预测尺寸与实际试验测得的焊缝尺寸误差分别为焊缝宽度5.4%和焊层高度6.6%. 对沉积成形的GH4169高温合金薄壁构件分别进行了水平方向和垂直方向的拉伸力学性能测试，其强度极限分别达到1 130.93和1 126.04 MPa，断后伸长率分别为18.1%和16.56%，断面收缩率分别达到20.6%和20.2%.Abstract: The ultra-high frequency pulsed gas tungsten arc welding process was optimized by response surface method(RSM). By establishing the functional relation, the regression model of weld bead size on welding current(Ib), wire feed speed(WFS) and travel speed(TS) is obtained, and the reliability of the regression model is verified by variance analysis. The corresponding welding parameters are selected by setting the optimization conditions and the size of weld bead is predicted. The error between the predicted size from the model and the actual size is 5.4% of bead width and 6.6% of bead height, respectively. After the deposition of thin-wall GH4169 superalloy part, the mechanical properties are tested, including the horizontal and vertical tensile properties, the ultimate strength are 1 130.93 MPa and 1 126.04 MPa, respectively, the elongation rate are 18.1% and 16.56%, respectively, the reduction of area are 20.6% and 20.2%, respectively.
-
0. 序言
电弧增材制造技术(wire and arc additive manufacturing, WAAM)作为一种非常有前景的增材制造方法，能够将传统氩弧焊的低成本、高效率等优点良好的结合起来，同时与MIG焊相比，以TIG作为热源的电弧增材制造工艺(gas tungsten arc welding, GTAW)过程更加稳定，且热输入相对更低，有利于得到成形质量更好的结构件[1-2].
WAAM工艺是一种多变量且耦合性较强的工艺过程，如焊接速度(v)、送丝速度(vs)、电流值大小(I)、电弧脉冲频率(f )等诸多因素可以影响到焊缝的形貌尺寸乃至整个结构件的最终成形质量[3]. 因此，对沉积过程进行路径规划以及焊接参数的优化是影响增材制造成形件质量的重要因素. Ding等人[4-6]通过模型计算和试验分析，对WAAM工艺进行路径规划，同时运用响应面法做了一部分焊接参数优化的相关工作，其研究结果指出，WAAM工艺往往对成形精度的要求比较高，这不仅关系到增材过程的沉积效率，同时也会影响成形件的综合性能表现. 基于优化后的焊缝截面模型，其指出对于多道搭接的增材路径，当相邻焊缝中心的距离约为焊缝宽度的73.8%时，沉积过程较稳定，成形件质量较好，并结合相关的经验公式优化焊接参数，沉积成形出了相应的叶轮构件，具有较大的参考价值. Fu等人[7]采用响应面法(response surface method，RSM)对电弧增材工艺进行了参数优化设计，以焊接速度、送丝速度、电弧脉冲时间和频率以及电压作为输入变量，运用Box-Behnken法得到五因素三水平的试验设计组，其结果表明，以优化后的焊接参数进行沉积的成形件具有良好的表面质量，焊缝尺寸波动小，材料组织均匀且具有较好的力学性能. Geng等人[8]运用响应面法建立焊接参数与焊缝尺寸之间预测模型，其预测的焊缝高度和焊缝宽度的数值大小与试验测得的实际焊缝数据误差分别为4.5%和7.1%，证明该方法的计算模型可靠有效.
通过响应面法对超高频电弧增材制造工艺进行了参数优化，对比了优化后的焊接参数成形所得到的的焊缝尺寸与理论尺寸的误差，并以此沉积成形得到GH4169高温合金薄壁构件，在进行热处理之后还测试了试样的力学性能，考察在优化参数下成形的构件，其力学性能如何，为后续超高频电弧增材工艺的制定提供参考依据.
1. 试验设计及工艺
1.1 试验设计
当试验过程中的参数变量与其响应变量存在非线性关系时，响应面法能够通过建立多元二次回归方程模型，拟合因子和响应量之间的函数关系，找到在已知优化范围内的最佳试验方案[9]. 试验运用Design-Expert软件，选取对焊缝形貌影响最为显著的3个因素—焊接电流(Ib)、送丝速度(vs)及焊接速度(vs)，作为输入变量，焊缝宽度(D)及焊层高度(H)作为响应量进行优化设计，然后以试验组参数沉积成形GH4169高温合金焊缝并统计尺寸数据，寻找相对最优的参数配比.
经过前期试验和选择，试验若采用中心复合设计(CCD)法对焊接参数进行设计，处于CCD空间模型轴点处的若干组焊接参数的数值，超出预先选定的优化范围过多，焊接参数的不匹配导致焊缝成形质量并不理想或单道焊缝的沉积过程难以顺利完成，故转而采用能够使参数范围合理且效率更高的Box-Bekhen(BBD)法，设计了三因素、三水平的试验组，所选的焊接参数及其数值范围如表1所示. 相关研究表明，电流频率在0 ~ 80 kHz范围内变化时，金属的熔深和熔宽在60 kHz时达到最大值[10]，这样有利于焊缝成形时截面轮廓呈较扁而平缓的抛物线状，有利于后续金属沉积层的熔覆. 超高频电流的频率若过大，则熔宽的下降可能会导致焊缝变细；频率过小则可能会影响超高频电流对成形件组织晶粒的细化作用，故此处选取脉冲频率(f )为60 kHz.
表 1 焊接参数及优化范围Table 1. Weld parameters and their limits焊接参数 优化范围 −1 0 1 基值电流Ib/A 160 200 240 送丝速度vs/(cm·min−1) 200 300 400 焊接速度v/(cm·min−1) 25 35 45 表1中焊接参数的选取主要以送丝速度为出发点，为提高电弧增材成形速率，根据试验经验，取送丝速度最小为200 cm/min. 试验所用的HPVP600A型号超高频脉冲焊接电源最大电流为300 A，因此当脉冲幅值为60 A时，最大基值电流为240 A. 该电弧增材工艺分为两个阶段，初始阶段在预热底板之后，为了使成形焊缝足够宽、后续成形的板件有效厚度能够保持不低于5 mm(根据航标板状拉伸试样所允许的最小厚度选取)，焊接电流需设到最大，焊接速度取30 cm/min，送丝速度为200 cm/min，待焊缝形貌稳定后，电流大小逐渐减至160 A以降低热输入，且根据此时电流的熔丝能力，送丝速度最高取400 cm/min，开始稳定的沉积阶段. 当送丝速度一定，焊接速度在25 ~ 45 cm/min范围内时，焊丝的熔覆过程相对稳定. 若送丝速度和焊接速度过大或电流过小，则会由于焊丝未及时熔覆而导致焊缝形貌变形，影响成形质量和薄壁件的有效厚度；若焊接速度过小或电流过大，则会显著增加系统的热输入，增加构件的残余应力，而且在送丝速度比较大而焊接速度较小的情况下，会出现“顶丝”的现象，焊丝直插进熔池，可能会造成送丝嘴甚至焊枪的位置偏移，从而影响弧长(一般地，钨极距离焊缝表面的距离，即弧长必须至少保持在大于等于5 mm的范围，金属的熔覆成形过程最稳定). 若设备熔丝能力较弱、送丝速度较小，才可以考虑保持弧长在3 mm左右，具体需要参考焊层高度来制定. 所以综合以上考虑，制定了表1的优化范围.
1.2 试验设备及材料
试验其它参数设置如表2所示. 设计后的试验组焊接参数如表3所示. 试验采用UHFP-GTAW工艺(ultra-high frequency pulsed gas tungsten arc welding, UHFP-GTAW)，焊机为HPVP600A型号超高频脉冲焊接电源，焊接设备为OTC六轴联动焊接机器人，焊丝采用ϕ1.2 mm的GH4169高温合金焊丝，底板为尺寸300 mm × 300 mm × 15 mm的低碳钢板，使用纯度99.99%的氩气作为保护气. 试验前底板须预热到至少200 ℃以尽量接近连续沉积时系统的热环境条件. 试验组焊缝的长度统一为10 cm，且每隔3 cm取一点测量其焊缝宽度及焊层高度，取3个点并计算平均值. 17组焊缝的平均尺寸数据如表3中的焊缝宽度及焊层高度所示.
表 2 试验参数设置Table 2. Parameters of power supply used in the experiments脉冲幅值Im/A 占空比δ(%) 弧长l/mm 焊接电流I/A 熄弧时间t1/s 预通气时间t2/s 滞后气时间t3/s 保护气流量Q/(L·min−1) 60 50 5.0 20 1.6 ~ 2.0 2.0 6.0 15 表 3 试验设计组参数及测量数据Table 3. Experimental design matrix and the measured data序号 编码矩阵 输入变量 响应量(mm) A：基值电流Ib/A B：送丝速度vs/(cm·min−1) C：焊接速度v/(cm·min−1) 焊缝宽度D 焊层高度H 1 0.000 0.000 0.000 200 300 35 6.12 2.34 2 −1.000 0.000 1.000 160 300 45 5.91 2.57 3 0.000 0.000 0.000 200 300 35 6.08 2.46 4 1.000 0.000 1.000 240 300 45 6.36 2.53 5 −1.000 1.000 0.000 160 400 35 6.18 2.84 6 0.000 0.000 0.000 200 300 35 6.23 2.44 7 0.000 0.000 0.000 200 300 35 6.2 2.48 8 1.000 1.000 0.000 240 400 35 6.33 2.6 9 0.000 1.000 −1.000 200 400 25 6.21 2.65 10 0.000 1.000 1.000 200 400 45 5.97 2.76 11 1.000 −1.000 0.000 240 200 35 6.13 2.34 12 −1.000 −1.000 0.000 160 200 35 5.86 2.36 13 0.000 0.000 0.000 200 300 35 6.15 2.52 14 1.000 0.000 −1.000 240 300 25 6.82 2.56 15 0.000 −1.000 1.000 200 200 45 5.94 2.23 16 −1.000 0.000 −1.000 160 300 25 6.4 2.53 17 0.000 −1.000 −1.000 200 200 25 6.01 2.12 2. 结果与讨论
2.1 数学模型建立与拟合结果分析
方差分析(analysis of variance，ANOVA)主要检验模型及其失拟度的显著性(significant or not significant)，根据Adeq. Precision值的大小判断模型的可行性. 而设计模型的建立主要依据表3中输入变量与响应量的数据，其函数关系可以统一表示为y = f(Ib，vs，v)，若将响应量y扩展为二阶多项式回归方程的形式，则如公式(1)所示，即
$$ y = {b_0} + \sum {{b_i}{x_i}} + \sum {{b_{ii}}x_i^2} + \sum {{b_{ij}}{x_i}{x_j}} $$ (1) 在计算得到各项系数之后，焊缝宽度和焊层高度与3个输入变量间的函数关系式分别如式(2)、式(3)所示，式中各系数已保留到小数点后两位.
$$ \begin{split} D = + 8.57 - 0.04{I_{\rm{b}}} + 0.01{v_{\rm{s}}} - 0.06v + 9.66 \times {10^{ - 5}}I_{\rm{b}}^2 - 1.86 \times {10^{ - 5}}{v_{\rm{s}}}^2 + 6.20 \times {20^{ - 4}}{v^2} \end{split} $$ (2) $$ \begin{split} H =& + 2.18 - 6.13 \times {10^{ - 3}}{I_{\rm{b}}} + 4.79 \times {10^{ - 3}}{v_{\rm{s}}} - 1.05 \times {10^{ - 3}}v + 4.38 \times {10^{ - 5}}{I_{\rm{b}}} v + \\& 1.86 \times {10^{ - 5}}I_{\rm{b}}^2 - 5.28 \times {10^{ - 6}}{v_{\rm{s}}}^2 + 9.75 \times {10^{ - 5}}{v^2} \end{split} $$ (3) 从表4中可以看出，焊缝宽度的模型F值为10.74，概率P > F的值为0.000 7(小于0.05)，故模型为显著，具有统计学意义，且拟合回归方程的决定系数R2值为0.865 7(> 0.80)，比较接近于1，从这两点来看说明模型的拟合方程可以接受. 失拟度(lack of fit)值为4.5，结果为不显著，说明模型可靠. 此外，拟合的结果还可以用预估决定系数R2(pred R-squared)和校正决定系数R2(adj R-squared)之间的接近程度来判断. 校正决定系数R2是扣除了回归方程中所受到的包含项数的影响的相关系数，因而可以更准确的反应模型的好坏[11]. 二者相差越小，说明模型越可靠. 表3中的Pred R-Squared和Adj R-Squared值分别为0.704 8和0.785 0，数值比较接近，从这一点看拟合方程同样可以接受. 在焊缝宽度的表达式中，A，B，C，A2，B2，C2为响应量的显著因素，AB，AC，BC的P值分别为0.63、0.91和0.50，为非显著因素，因此在model选项卡中将其消去，以确保模型精度. 模型的信噪比(signal to noise ratio)Adeq Precision值的大小须大于4方可接受，从表4可知，焊缝宽度的回归模型信噪比为13.365，故该模型可以用于预测.同理可以分析焊层高度的回归模型方差结果，如表5所示. 焊层高度的模型F值为15.28，概率P > F的值为0.000 2(小于0.05)，模型为显著，拟合回归方程的决定系数R2值为0.922 4(> 0.80)，接近于1，说明模型的拟合方程可以接受. 失拟度值为0.86，结果为不显著，说明模型可靠. 预估决定系数和校正决定系数分别为0.748 6和0.862 0，数值比较接近，从这一点看拟合方程同样可以接受. 在焊层高度的表达式中，A，B，C，AC，A2，B2，C2为响应量的显著因素，AB项和BC项的P值分别为0.84和0.49，为非显著因素，因此在model选项卡中将其消去，以确保模型精度. 焊层高度的回归模型信噪比为11.424，同样可用于预测.
表 4 焊缝宽度的回归模型方差分析结果Table 4. Resulting ANOVA table for regression model of bead width D来源 平方和 自由度 均方 模型显著性F 失拟项 P > F 模型 Model 0.73 6 0.12 10.74 0.000 7 (显著) A-Ib 0.21 1 0.21 18.47 0.001 6 B-vs 0.07 1 0.07 6.24 0.031 5 C-v 0.20 1 0.20 17.63 0.001 8 A2 0.10 1 0.10 8.93 0.013 6 B2 0.14 1 0.14 12.87 0.005 0 C2 0.016 1 0.016 1.44 0.058 2 残差 0.11 10 0.011 失拟度 0.098 6 0.016 4.50 0.083 5 (不显著) 绝对误差 0.015 4 3.63 × 10−3 总离差 0.84 16 标准差 0.11 决定系数 0.865 7 均值 6.17 校正决定系数 0.785 0 试验精确度 1.72 预估决定系数 0.704 8 权重 0.41 信噪比 13.365 表 5 焊层高度的回归模型方差分析结果Table 5. Resulting ANOVA table for regression model of bead height H来源 平方和 自由度 均方 模型显著性 F 失拟项 P > F 模型 0.23 7 0.033 15.28 0.000 2 (显著) A-Ib 6.125 × 10−4 1 6.125 × 10−4 0.29 0.005 6 B-vs 0.21 1 0.21 98.74 < 0.000 1 C-v 6.125 × 10−4 1 6.125 × 10−4 0.29 0.005 6 AC 1.225 × 10−3 1 1.225 × 10−3 0.57 0.03 4 A2 3.727 × 10−3 1 3.727 × 10−3 1.74 0.019 5 B2 0.012 1 0.012 5.48 0.044 0 C2 4.003 × 10−4 1 4.003 × 10−4 0.19 0.075 5 残差 0.019 9 2.139 × 10−3 失拟度 9.975 × 10−3 5 1.995 × 10−3 0.86 0.574 1 (不显著) 绝对误差 9.280 × 10−3 4 2.320 × 10−3 标准差 0.046 决定系数 0.922 4 均值 2.50 预估决定系数 0.862 0 试验精确度 1.85 预估决定系数 0.748 6 权重 0.062 信噪比 11.424 图1为焊缝宽度与焊层高度模型的残差正态概率分布，从图中可以看出，两个模型的残差分布均近似沿着一条直线，说明回归模型拟合得较好，误差分布较均匀，没有偏差较大的奇异点，模型可以较准确地预测响应量值. 为了能够更准确地预测焊缝尺寸随焊接参数变化的趋势，还需要了解各输入变量及其交互项(如AB，AC，BC等)对响应量本质的影响，一方面这样有助于优化靠近上述中心点附近的设计区域，另一方面当试验中的焊缝几何尺寸偏离预定尺寸时，变量的分析可以为焊接参数的微调提供理论指导. 如图2所示，图2a，2b分别给出的是焊缝宽度和焊层高度在各输入变量偏离中心点后，其对应的变化趋势. 图2a中，基值电流Ib(A)和焊接速度vs(C)对焊缝宽度的影响呈相反的趋势，当A值偏离中心参照点时，随着电流的增大，焊缝宽度逐渐增大，而当焊接速度升高时，焊缝宽度大小则呈现递减的趋势，送丝速度对焊缝宽度的影响趋势较平缓，随着送丝速度的增加，焊缝宽度略呈现先增大后减小的趋势. 同理，从图2b中可以看出，电流和焊接速度的大小对焊层高度的影响较平缓，H值的波动主要来源于送丝速度的变化，当送丝速度偏离中心点的程度增大时，B值越大，则焊层高度越大，反之，值越小.
![]()
图 1 模型残差的正态概率分布Figure 1. Normal probability plot of residuals for the model. (a) weld width; (b) welding layer height![]()
图 2 焊缝宽度和焊层高度分别作为中心参照点偏离量的函数扰动趋势图Figure 2. Plot of width and height perturbation as a function of deviation from reference point respectively. (a) weld width; (b) weld layer height2.2 焊接参数的择优选取
在分析和验证模型的可靠性之后，对焊接参数进行优化. 为减少焊缝沉积成形过程中的热输入，对电流的期望是尽量将其减小，故在“Criteria”选项卡中设置基值电流Ib为minimize；为提高沉积效率，送丝速度设为maximize；焊接速度在优化范围选取即可保证沉积过程的稳定进行，设为“in range”. 该条件下方案的可行性指数分布如图3所示，在靠近图中的红色区域处取得最优参数，方案可行性值为1. 以此条件优化后得到的结果为基值电流为180.00 A，送丝速度为400.00 cm/min，焊接速度为33.10 cm/min，预测的焊缝宽度为6.054 mm，焊层高度为2.628 mm. 经试验验证，该参数下沉积成形的焊缝形貌及尺寸如图4所示. 其焊缝宽度和焊层高度分别为6.381和2.454 mm，与优化模型预测出的尺寸偏差分别为5.4%和6.6%，误差大小可以接受，证明优化结果可靠.
![]()
图 3 当焊接速度v= 33.10 cm/min时，送丝速度和基值电流对方案可行性的影响Figure 3. Effect of base current and wire feed speed on desirability while v = 33.10 cm/min. (a) three-dimensional pattern of desire probability; (b) contour map of desire probability![]()
图 4 Ib = 180.00 A，vs = 400.00 cm/min，v = 33.10 cm/min的条件下，焊缝截面尺寸的光镜照片Figure 4. Cross-section OM image of single-layer figuration while the optimized parameters are used: Ib = 180.00 A, vs = 400.00 cm/min, v = 33.10 cm/min2.3 构件成形及性能测试
以优化后的焊接参数：Ib = 180.00 A，vs = 400.00 cm/min，v = 33.10 cm/min，其它参数按表2设置，沉积成形尺寸为100 mm × 100 mm × 6 mm的薄壁构件，如图5a所示. 成形件实际厚度略大于6 mm，在优化范围内，薄壁件的侧面平整度较好，但由于过热仍有较多不平整的地方，侧壁层层堆积的结构特点十分明显. 在对薄壁件进行了GH4169高温合金的标准固溶时效热处理之后，还对其力学性能进行了测试，测试试样如图5b所示. 试验测得的构件拉伸力学性能结果如表6.
![]()
图 5 采用优化参数成形的GH4169高温合金薄壁件和拉伸力学试样Figure 5. Thin-wall part of GH4169 superalloy with the optimized parameters and the tensile test specimens. (a) morphology of forming part; (b) tensile test specimens表 6 用优化参数成形的GH4169薄壁件力学测试结果Table 6. Results of tensile test of GH4169 thin-wall part deposited with optimized parameters取样方向 屈服强度R0.2/MPa 强度极限Rm/MPa 断后伸长率A(%) 断面收缩率Z(%) 横向(H) 902.57 1 130.93 18.1 20.6 纵向(Z) 890.87 1 126.04 16.56 20.2 拉伸试样分别为横向和纵向，即焊接速度方向和垂直沉积方向. 由表6可以看到，构件在水平方向(H)和垂直方向(Z)上强度极限的平均值分别达到了1 130.93和1 126.04 MPa，高于铸件的性能，但与锻件性能相差约300 MPa左右的水平. 断后伸长率和断面收缩率平均在20%左右，塑性良好. 表中数据均为拉伸试验结果的平均值，为验证数据结果的可靠性，还分别计算了两组试样的屈服强度、强度极限、断后伸长率和断面收缩率的标准方差，其标准差结果依次为：横向1.73/3.92/1.98/0.49；纵向0.06/0.49/1.16/0.07，数据波动均在可接受范围内，证明结果可靠.
3. 结论
(1) 文中建立了焊接参数与焊缝尺寸之间的回归模型，计算了各输入变量对响应量的耦合作用，并通过方差分析验证了该模型的可靠性. 计算得到优化后的焊接参数为基值电流Ib = 180.00A，送丝速度vs = 400.00 cm/min，焊接速度v = 33.10 cm/min，并进行了试验验证. 验证结果表明，模型预测的焊缝宽度和焊层高度与试验测得的相应数据误差分别为5.4%和6.6%.
(2) 以择优参数成形了GH4169高温合金薄壁件，并测试了其拉伸力学性能. 构件在水平方向与垂直方向强度极限的平均水平分别达到了1 130.93和1 126.04 MPa，高于铸件的性能且较接近锻件水平，塑性较好.
-
![]()
图 1 模型残差的正态概率分布
Figure 1. Normal probability plot of residuals for the model. (a) weld width; (b) welding layer height
![]()
图 2 焊缝宽度和焊层高度分别作为中心参照点偏离量的函数扰动趋势图
Figure 2. Plot of width and height perturbation as a function of deviation from reference point respectively. (a) weld width; (b) weld layer height
![]()
图 3 当焊接速度v= 33.10 cm/min时，送丝速度和基值电流对方案可行性的影响
Figure 3. Effect of base current and wire feed speed on desirability while v = 33.10 cm/min. (a) three-dimensional pattern of desire probability; (b) contour map of desire probability
![]()
图 4 Ib = 180.00 A，vs = 400.00 cm/min，v = 33.10 cm/min的条件下，焊缝截面尺寸的光镜照片
Figure 4. Cross-section OM image of single-layer figuration while the optimized parameters are used: Ib = 180.00 A, vs = 400.00 cm/min, v = 33.10 cm/min
![]()
图 5 采用优化参数成形的GH4169高温合金薄壁件和拉伸力学试样
Figure 5. Thin-wall part of GH4169 superalloy with the optimized parameters and the tensile test specimens. (a) morphology of forming part; (b) tensile test specimens
表 1 焊接参数及优化范围
Table 1 Weld parameters and their limits
焊接参数 优化范围 −1 0 1 基值电流Ib/A 160 200 240 送丝速度vs/(cm·min−1) 200 300 400 焊接速度v/(cm·min−1) 25 35 45 
下载: 导出CSV
表 2 试验参数设置
Table 2 Parameters of power supply used in the experiments
脉冲幅值Im/A 占空比δ(%) 弧长l/mm 焊接电流I/A 熄弧时间t1/s 预通气时间t2/s 滞后气时间t3/s 保护气流量Q/(L·min−1) 60 50 5.0 20 1.6 ~ 2.0 2.0 6.0 15
下载: 导出CSV
表 3 试验设计组参数及测量数据
Table 3 Experimental design matrix and the measured data
序号 编码矩阵 输入变量 响应量(mm) A：基值电流Ib/A B：送丝速度vs/(cm·min−1) C：焊接速度v/(cm·min−1) 焊缝宽度D 焊层高度H 1 0.000 0.000 0.000 200 300 35 6.12 2.34 2 −1.000 0.000 1.000 160 300 45 5.91 2.57 3 0.000 0.000 0.000 200 300 35 6.08 2.46 4 1.000 0.000 1.000 240 300 45 6.36 2.53 5 −1.000 1.000 0.000 160 400 35 6.18 2.84 6 0.000 0.000 0.000 200 300 35 6.23 2.44 7 0.000 0.000 0.000 200 300 35 6.2 2.48 8 1.000 1.000 0.000 240 400 35 6.33 2.6 9 0.000 1.000 −1.000 200 400 25 6.21 2.65 10 0.000 1.000 1.000 200 400 45 5.97 2.76 11 1.000 −1.000 0.000 240 200 35 6.13 2.34 12 −1.000 −1.000 0.000 160 200 35 5.86 2.36 13 0.000 0.000 0.000 200 300 35 6.15 2.52 14 1.000 0.000 −1.000 240 300 25 6.82 2.56 15 0.000 −1.000 1.000 200 200 45 5.94 2.23 16 −1.000 0.000 −1.000 160 300 25 6.4 2.53 17 0.000 −1.000 −1.000 200 200 25 6.01 2.12
下载: 导出CSV
表 4 焊缝宽度的回归模型方差分析结果
Table 4 Resulting ANOVA table for regression model of bead width D
来源 平方和 自由度 均方 模型显著性F 失拟项 P > F 模型 Model 0.73 6 0.12 10.74 0.000 7 (显著) A-Ib 0.21 1 0.21 18.47 0.001 6 B-vs 0.07 1 0.07 6.24 0.031 5 C-v 0.20 1 0.20 17.63 0.001 8 A2 0.10 1 0.10 8.93 0.013 6 B2 0.14 1 0.14 12.87 0.005 0 C2 0.016 1 0.016 1.44 0.058 2 残差 0.11 10 0.011 失拟度 0.098 6 0.016 4.50 0.083 5 (不显著) 绝对误差 0.015 4 3.63 × 10−3 总离差 0.84 16 标准差 0.11 决定系数 0.865 7 均值 6.17 校正决定系数 0.785 0 试验精确度 1.72 预估决定系数 0.704 8 权重 0.41 信噪比 13.365
下载: 导出CSV
表 5 焊层高度的回归模型方差分析结果
Table 5 Resulting ANOVA table for regression model of bead height H
来源 平方和 自由度 均方 模型显著性 F 失拟项 P > F 模型 0.23 7 0.033 15.28 0.000 2 (显著) A-Ib 6.125 × 10−4 1 6.125 × 10−4 0.29 0.005 6 B-vs 0.21 1 0.21 98.74 < 0.000 1 C-v 6.125 × 10−4 1 6.125 × 10−4 0.29 0.005 6 AC 1.225 × 10−3 1 1.225 × 10−3 0.57 0.03 4 A2 3.727 × 10−3 1 3.727 × 10−3 1.74 0.019 5 B2 0.012 1 0.012 5.48 0.044 0 C2 4.003 × 10−4 1 4.003 × 10−4 0.19 0.075 5 残差 0.019 9 2.139 × 10−3 失拟度 9.975 × 10−3 5 1.995 × 10−3 0.86 0.574 1 (不显著) 绝对误差 9.280 × 10−3 4 2.320 × 10−3 标准差 0.046 决定系数 0.922 4 均值 2.50 预估决定系数 0.862 0 试验精确度 1.85 预估决定系数 0.748 6 权重 0.062 信噪比 11.424
下载: 导出CSV
表 6 用优化参数成形的GH4169薄壁件力学测试结果
Table 6 Results of tensile test of GH4169 thin-wall part deposited with optimized parameters
取样方向 屈服强度R0.2/MPa 强度极限Rm/MPa 断后伸长率A(%) 断面收缩率Z(%) 横向(H) 902.57 1 130.93 18.1 20.6 纵向(Z) 890.87 1 126.04 16.56 20.2
下载: 导出CSV
-
[1] Daniel Clark, Martin R Bache, Mark T Whittaker, et al. Microstructural characterization of a polycrystalline nickel based superalloy processed via tungsten inert gas shaped metal deposition[J]. Metallurgical and Material S Transactions B, 2010, 41B: 1346 − 1353.
[2] Alessandro Busachia, John Erkoyuncua, Paul Colegroveb, et al. Designing a WAAM based manufacturing system for defence applications[J]. Procedia CIRP, 2015, 37: 48-53.
[3] Jun Xiong, Ziqiu Yin, Weihua Zhang, et al. Closed-loop control of variable layer width for thin-walled parts in wire and arc additive manufacturing[J]. Journal of Materials Processing Technology, 2016, 233: 100 − 106. doi: 10.1016/j.jmatprotec.2016.02.021
[4] Ding Donghong, Pan Zengxi, Dominic Cuiuri , et al. A practical path planning methodology for wire and arc additive manufacturing of thin-wall structures[J]. Robotics and Computer Integrated Manufacturing, 2015, 34: 8 − 19. doi: 10.1016/j.rcim.2015.01.003
[5] Ding Donghong, Pan Zengxi, Dominic Cuiuri, et al. Bead modelling and implementation of adaptive MAT path in wire and arc additive manufacturing[J]. Robotics and Computer-Integrated Manufacturing, 2016, 39: 32 − 42. doi: 10.1016/j.rcim.2015.12.004
[6] Ding Donghong, Pan Zengxi, Dominic Cuiuri, et al. Process planning strategy for wire and arc additive manufacturing[J]. Robotics Welding, Intelligence and Automation, 2015, 363: 437 − 449.
[7] Fu Youheng, Wang Guilan, Zhang Haiou, et al. Optimization of surface appearance for wire and arc additive manufacturing of Bainite steel[J]. Internation Journal of Advanced Manufacture Technology, 2017, 91: 301 − 313. doi: 10.1007/s00170-016-9621-1
[8] Geng Haibin, Xiong Jiangtao, Huang Dan, et al. A prediction model of layer geometric size in wire and arc additive manufacturing using response surface methodology[J]. Internation Journal of Advanced Manufacture Technology, 2015, 93: 175 − 186.
[9] Lin W S, Lee B Y, Wu C L. Modeling the surface roughness and cutting force for turning[J]. Materials Process Technology, 2001, 108: 286 − 293. doi: 10.1016/S0924-0136(00)00835-9
[10] 李玉龙, 从保强, 杨明轩, 等. 2219-T87高强铝合金HPVP-GTAW焊缝成型参数[J]. 北京航空航天大学学报, 2014, 40(5): 712 − 716. Li Yulong, Cong Baoqiang, Yang Mingxuan, et al. Well arrearance of 2219-T87 high strenght aluminum alloy produced by HPVP-GTAW process[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(5): 712 − 716.
[11] 徐茂, 刘双宇, 李彦清, 等. 基于响应面法的SPCC与65Mn异种金属激光焊接工艺参数优化[J]. 应用激光, 2017, 37(3): 362 − 366. Xu mao, Liu Shuangyu, Li Yanqing, et al. Optimization of SPCC and 65Mn dissimilar metal laser welding process parameters based on response surface methodology[J]. Applied Laser, 2017, 37(3): 362 − 366.
-
期刊类型引用(8)
1. 刘景城，叶晗哲，徐贵峰，娄昊，耿海滨. 不同基板热沉的铝合金电弧增材控形. 福州大学学报(自然科学版). 2024(01): 91-97 . 
百度学术
2. 齐膑，余圣甫，何天英，刘曙. 多向钢节点电弧增材制造摆动工艺参数优化. 机械设计与制造. 2024(03): 119-124 . 百度学术
3. 崔宝磊，刘伟军，卞宏友. 基于响应面法的TiAl合金激光增材制造工艺参数优化. 应用激光. 2024(03): 13-21 . 百度学术
4. 郭志永，李猛，张志强，路学成，张天刚，曹轶然. 基于响应面法的镍基高温合金GH4169电弧增材工艺优化. 材料导报. 2024(19): 209-215 . 百度学术
5. 朱禹，陈菊芳，李小平，彭天豪. 电弧增材制造技术研究进展. 江苏理工学院学报. 2023(02): 85-92 . 百度学术
6. 朱禹，陈菊芳，李小平，彭天豪. 响应面法在H13模具钢电弧增材工艺参数优化中的应用. 工具技术. 2023(10): 21-27 . 百度学术
7. 宋少东，王燕燕，舒林森，何雅娟. 基于RSM-PSO的6061铝合金激光焊接工艺优化. 激光与光电子学进展. 2022(17): 227-233 . 百度学术
8. 熊明林，杨颖，汪昊，游书婷，宋冬寒. 基于响应面法的凝析气净化装置运行参数优化. 中小企业管理与科技(中旬刊). 2021(09): 191-193 . 百度学术
其他类型引用(7)
计量
- 文章访问数: 295
- HTML全文浏览量: 46
- PDF下载量: 20
- 被引次数: 15
