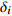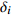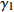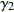基于主成分及灰色关联度分析的5083铝合金FSW接头工艺参数优化

陈兴惠; 张洪申

doi:10.12073/j.hjxb.20220623001

基于主成分及灰色关联度分析的5083铝合金FSW接头工艺参数优化

陈兴惠,
张洪申^,

昆明理工大学, 机电工程学院, 昆明, 650500

基金项目: 国家自然科学基金资助项目(50245036)

详细信息

作者简介:
陈兴惠，硕士，主要研究方向为材料连接技术；Email: 1136569171@qq.com

通讯作者:
张洪申，副教授；Email: hongshen@kust.edu.cn

中图分类号: TG 457
计量
- 文章访问数: 372
- HTML全文浏览量: 98
- PDF下载量: 72
出版历程
- 收稿日期: 2022-06-22
- 网络出版日期: 2023-04-05
- 刊出日期: 2023-05-24

Process parameters optimization of 5083 aluminum alloy FSW joint based on principal component analysis and grey correlation analysis

CHEN Xinghui,
ZHANG Hongshen^,

School of Electrical and Mechanical Engineering, Kunming University of Science and Technology, Kunming, 650500, China

摘要

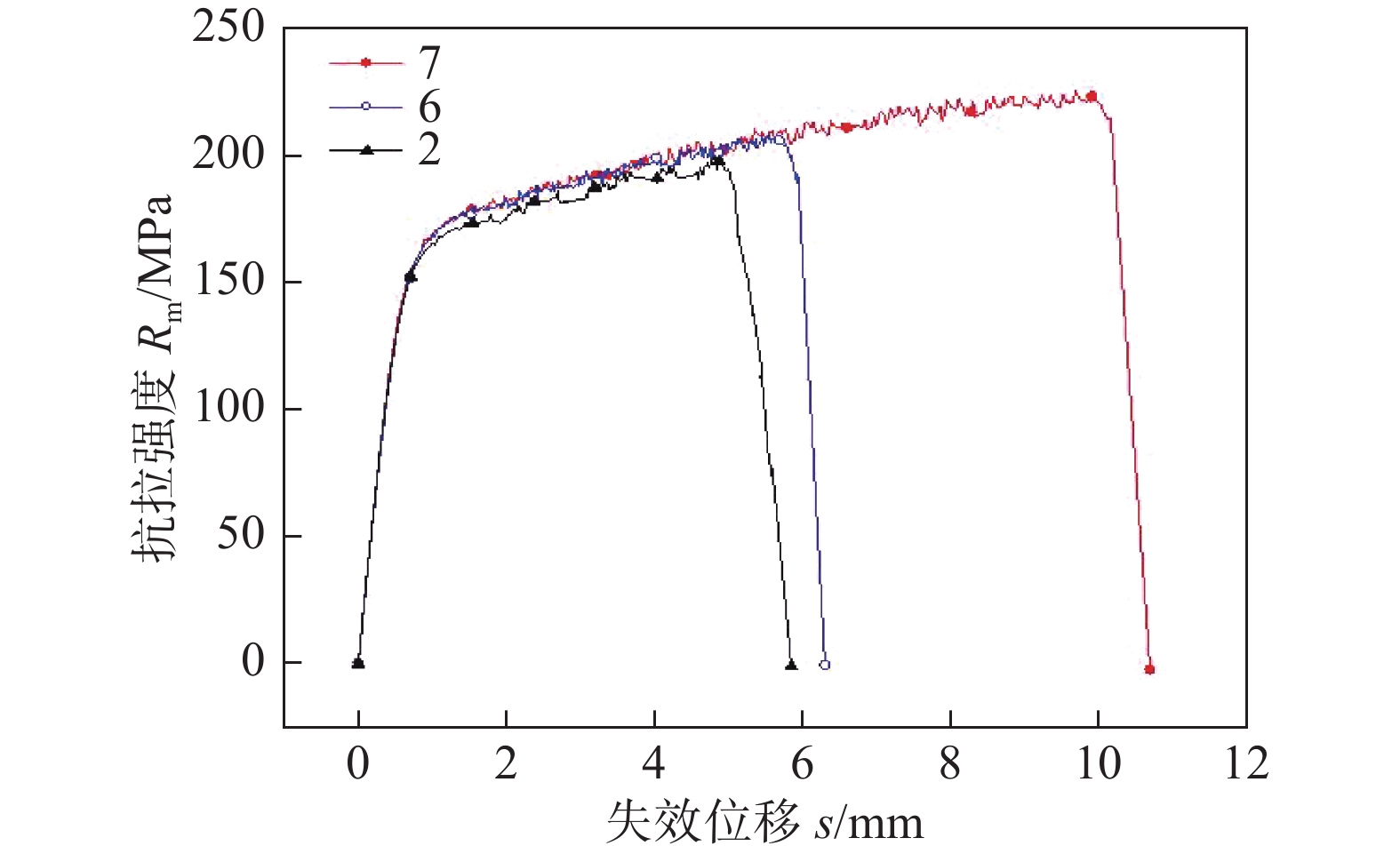
摘要: 针对铝合金搅拌摩擦焊接工艺参数优化问题，对5083铝合金板材进行研究，开展其在不同搅拌摩擦焊工艺参数下的力学性能探索，运用主成分分析和灰色关联度分析法对试验结果进行探索，得出焊接接头最优工艺参数，并建立基于GRG的工艺参数二阶预测模型.结果表明，均值极差法得出最优工艺参数组合为转速1 400 r/min，焊接速度1 mm/s，下压量0.3 mm，接头抗拉强度最大达到225.5 MPa，达到了母材的95.4％，失效位移为10.6 mm. 在试验工艺参数范围内，影响接头抗拉强度的主要因素次序为下压量、焊接速度、转速；模型预测值与计算值无显著差异，回归模型与试验数据的吻合度好，说明预测模型可靠度高，此回归模型可作为其预测模型.
- 5083铝合金 /
- 工艺参数 /
- 灰色关联度 /
- 抗拉强度
Abstract: Aim at optimizing the friction stir welding (FSW) process parameters of aluminum alloy, 5083 aluminum alloy plate was selected as the research object in this study. The mechanical properties of 5083 aluminum alloy plate under different FSW process parameters were explored. Principal component analysis (PCA) and grey relational degree (GRG) analysis were employed to analyze the test results. The optimal process parameters were obtained, and a second-order prediction model of process parameters based on GRG was established. The results show that the optimal combination of process parameters is a rotation speed of 1400 r/min, welding speed of 1 mm/s and plunge depth of 0.3 mm. The maximum tensile strength of the joint reaches 225.5 MPa, 95.4% of the base metal, and the failure displacement is 10.6 mm. Among the tested process parameters, the main factors influencing the tensile strength of the joint are plunge depth of shoulder, welding speed and rotation speed in sequence. Besides, there is no significant difference between the predicted value of the model and the calculated value. The good agreement between the regression model and the experimental data indicates that the prediction model has high reliability. The regression model can be used as the prediction model.
- 5083 aluminum alloy /
- process parameters /
- grey relational degree /
- tensile strength

HTML全文

图 1 灰色关联度随因素水平变化趋势图

Figure 1. Trend of grey correlation degree with factor level

下载: 全尺寸图片幻灯片

图 2 载荷—位移曲线图

Figure 2. Load—displacement curve

下载: 全尺寸图片幻灯片

图 3 9组参数下接头的拉伸性能

Figure 3. Tensile properties of joints under 9 groups of parameters

下载: 全尺寸图片幻灯片

图 4 不同工艺参数下接头宏观断口形貌图

Figure 4. Macro fracture morphology of joint under different process parameters. (a) front; (b) back

下载: 全尺寸图片幻灯片

图 5 GRG的预测值与实际值分布图

Figure 5. Distribution of predicted and actual GRG values

下载: 全尺寸图片幻灯片

图 6 GRG预测模型残差图

Figure 6. Residual graph of GRG prediction model

下载: 全尺寸图片幻灯片

表 1 5083铝合金力学性能

Table 1 Mechanical properties of 5083 aluminum alloy

抗拉强度R_m /MPa	断后伸长率A(%)
≥236	≥12

下载: 导出CSV

表 2 5083铝合金化学成分(质量分数，%)

Table 2 Chemical compositions of 5083 aluminum alloy

Si	Cu	Mg	Zn	Mn	Ti	Cr	Fe	其他	Al
<0.4	<0.1	4.0 ~ 4.9	<0.25	0.4 ~ 1.0	<0.15	0.05 ~ 0.25	<0.4	0.15	余量

下载: 导出CSV

表 3 正交试验因素及水平

Table 3 Orthogonal test factors and levels

水平	转速A(n)/ (r·min⁻¹)	焊接速度B(v)/ (mm·s⁻¹)	下压量C(H)/ mm
1	1 000	1	0.20
2	1 200	2	0.25
3	1 400	3	0.30

下载: 导出CSV

表 4 拉伸试验结果

Table 4 Test result

试验序号	转速A(n)/(r·min⁻¹)	焊接速度B(v)/(mm·s⁻¹)	下压量C(H)/mm	平均抗拉强度R_m/MPa	能量吸收平均值S/J
1	1 000	1	0.2	217.8	142.3
2	1 000	2	0.25	202.1	64.6
3	1 000	3	0.3	215.2	100.1
4	1 200	1	0.25	219	126.9
5	1 200	2	0.3	221.8	131.3
6	1 200	3	0.2	208.8	63.9
7	1 400	1	0.3	222.7	122.7
8	1 400	2	0.2	214.5	93.9
9	1 400	3	0.25	211.4	204.1

下载: 导出CSV

表 5 主成分计算结果

Table 5 Calculation results of principal component

成分	特征值	贡献率W_k(%)
第一主成分	1.159	57.94
第二主成分	0.841	42.06
累积贡献率(%)		100

下载: 导出CSV

表 6 灰色关联度分析结果

Table 6 Results of grey correlation analysis

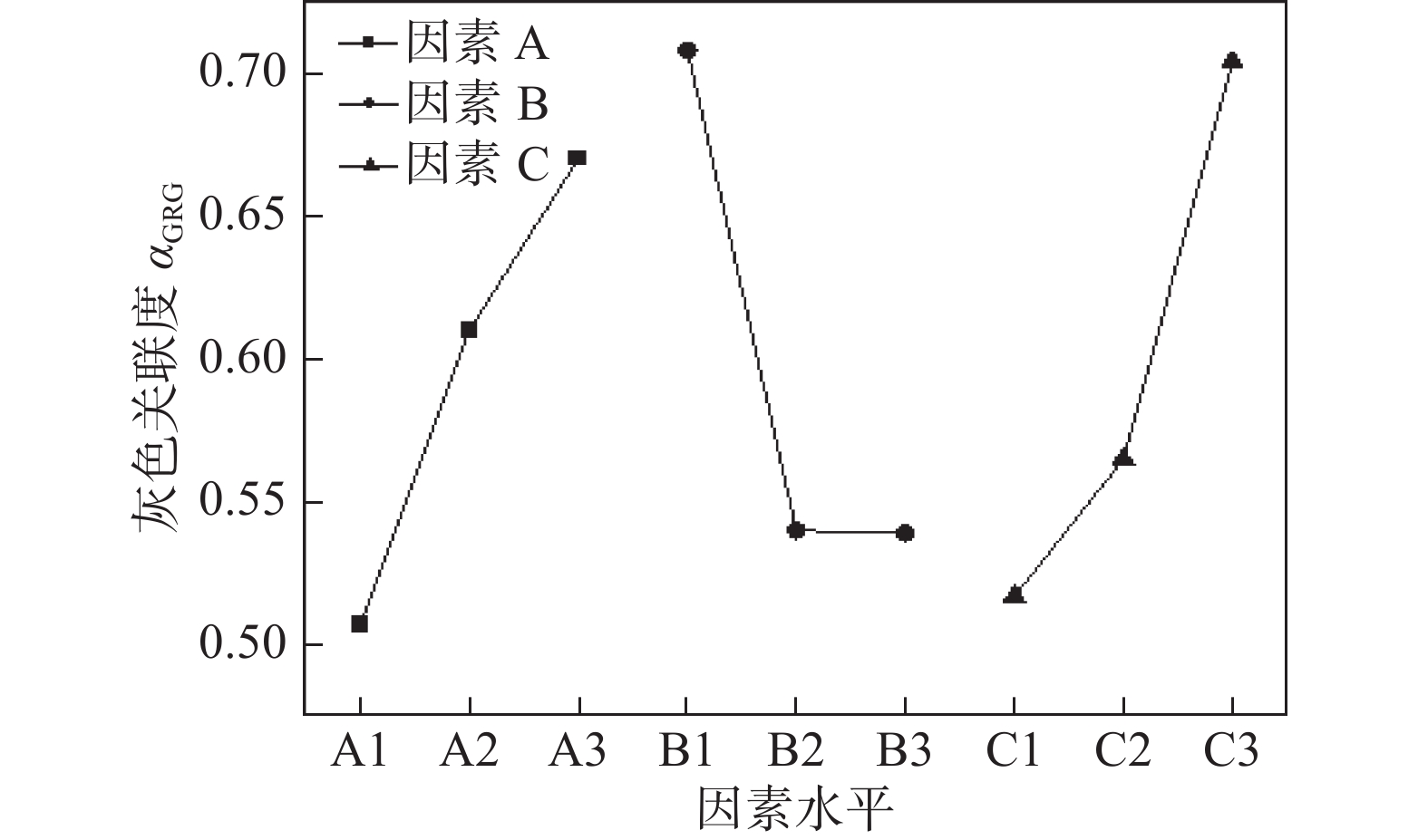
试验	抗拉强度			能量吸收值			灰色关联度$ \alpha_{{\rm{G R G}}}$	排序
试验	信噪比	$y_i$	$\delta_ i$	信噪比	$y_i$	$\delta_ i$	灰色关联度$ \alpha_{{\rm{G R G}}}$	排序
1	46.76	0.773	0.687	43.06	0.689	0.616	0.657	5
2	46.11	0	0.333	36.21	0.009	0.335	0.333	9
3	46.66	0.655	0.591	40.01	0.387	0.449	0.531	6
4	46.81	0.833	0.749	42.07	0.591	0.55	0.665	4
5	46.92	0.964	0.932	42.37	0.62	0.568	0.778	2
6	46.39	0.333	0.428	36.11	0	0.333	0.388	8
7	46.95	1	1	41.78	0.562	0.533	0.803	1
8	46.63	0.619	0.567	39.45	0.331	0.427	0.508	7
9	46.50	0.464	0.482	46.20	1	1	0.699	3

下载: 导出CSV

表 7 灰色关联度均值极差分析

Table 7 Mean range analysis of grey correlation degree

项目	转速 A(n)/(r·min⁻¹)	焊接速度 B(v)/(mm·s⁻¹)	下压量 C(H)/mm
$ \gamma_ 1 $	0.507	0.708	0.517
$ \gamma _2 $	0.61	0.54	0.565
$ \gamma _3 $	0.67	0.539	0.704
极差	0.163	0.169	0.187

下载: 导出CSV

表 8 预测模型的方差分析结果

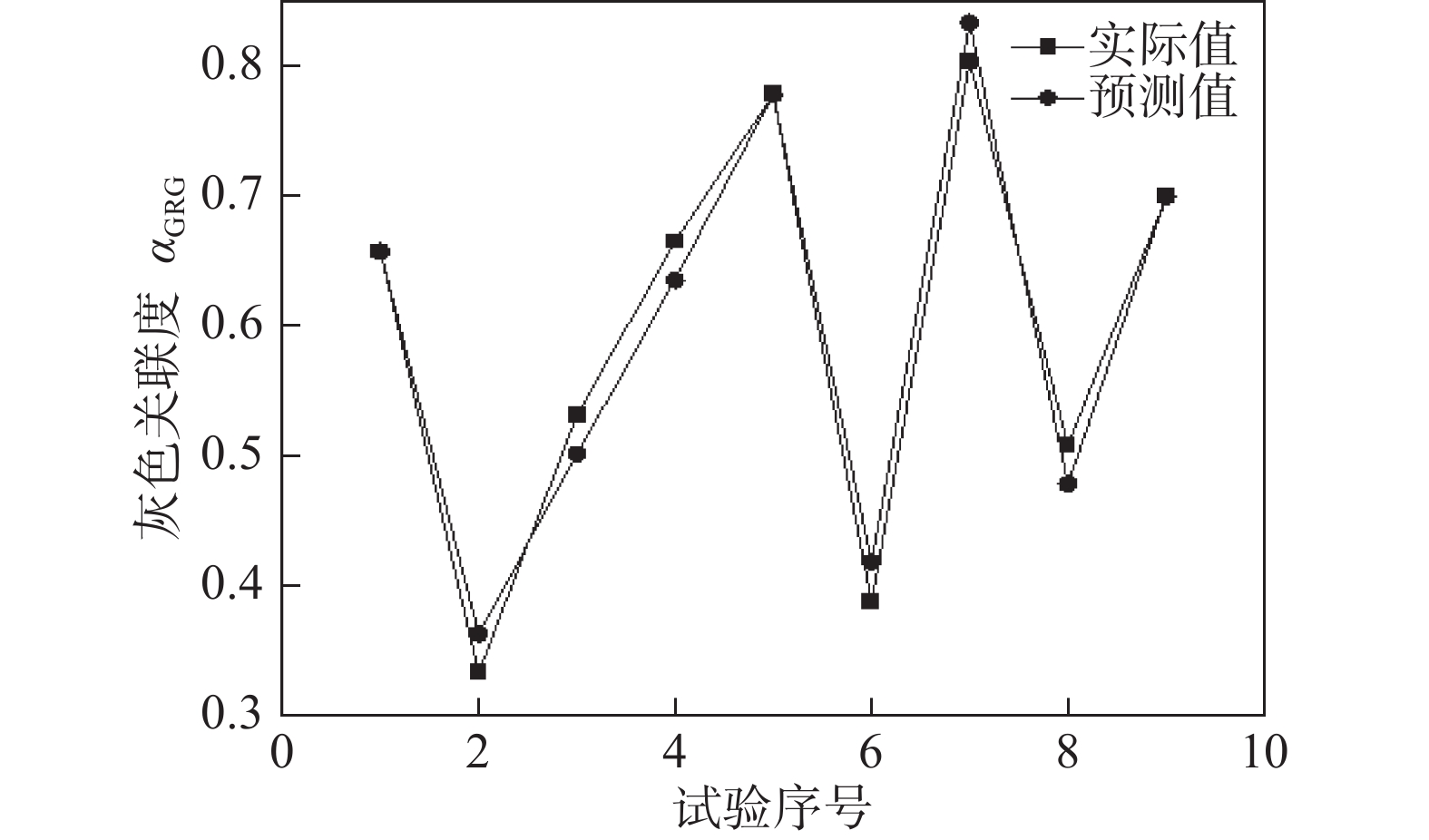
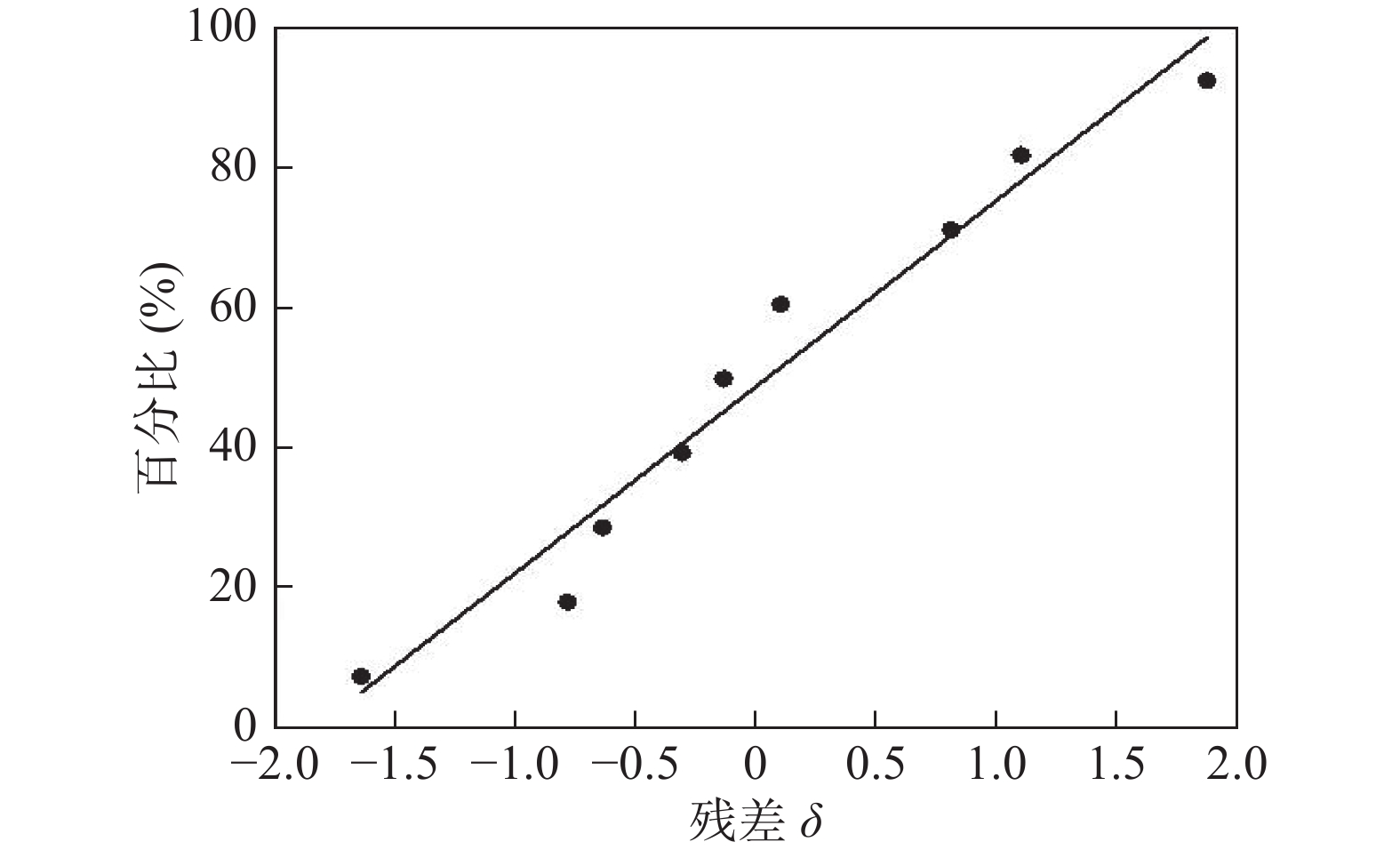
Table 8 Variance analysis results of the prediction model

参数	自由度df	平方和ss	均方ms	F值	显著性
回归平方和	7	0.214 066	0.030 581	5.66	是
残差平方和	1	0.193 575	0.064 525
总和	8
标准差SD = 0.0734847		R-Sq = 97.54%		R-Sq(adj) = 80.32%

下载: 导出CSV

参考文献(23)

[1]	方远方, 张华. 厚板5083铝合金搅拌摩擦焊接头沿厚度方向组织与力学性能[J]. 机械工程学报, 2022, 58(4): 94 − 101. Fang Yuanfang, Zhang Hua. Microstructure and mechanical properties of friction stir welded joint of thick plate 5083 aluminum alloy along thickness direction[J]. Journal of Mechanical Engineering, 2022, 58(4): 94 − 101.
[2]	Rao D, Huber K, Heerens J, et al. Asymmetric mechanical properties and tensile behaviour prediction of aluminium alloy 5083 friction stir welding joints[J]. Materials Science & Engineering A, 2013, 565: 44 − 50.
[3]	Mishra R S, Ma Z Y. Friction stir welding and processing[J]. Materials Science and Engineering:Reports, 2005, 50(1-2): 1 − 78. doi: 10.1016/j.mser.2005.07.001
[4]	张华, 秦海龙, 吴会强. 工艺参数对2195铝锂合金搅拌摩擦焊接头力学性能的影响[J]. 焊接学报, 2016, 37(4): 19 − 23. Zhang Hua, Qin Hailong, Wu Huiqiang. Effect of process parameters on mechanical properties of friction stir welded joints of 2195 Al-Li alloy[J]. Transactions of the China Welding Institution, 2016, 37(4): 19 − 23.
[5]	范文学, 陈芙蓉. 基于响应面法7A52高强铝合金FSW接头抗拉强度预测及优化[J]. 焊接学报, 2021, 42(9): 55 − 60. doi: 10.12073/j.hjxb.20210322001 Fan Wenxue, Chen Furong. Prediction and optimization of tensile strength of FSW joint of 7A52 high strength aluminum alloy based on response surface method[J]. Transactions of the China Welding Institution, 2021, 42(9): 55 − 60. doi: 10.12073/j.hjxb.20210322001
[6]	Abuajila R, Vidosav M, Aleksandar S, et al. Optimization of AA5083 friction stir welding parameters using Taguchi method[J]. Technical Gazette, 2018, 25(3): 861 − 866.
[7]	Anil R, Kumar P J, Anil M R, et al. Optimization of friction stir welding parameters during joining of AA3103 and AA7075 aluminium alloys using Taguchi method[J]. Materials Today:proceedings, 2021, 46(17): 7733 − 7739.
[8]	周海波, 浦娟, 龙伟民, 等. 基于田口法的高硅铝合金超高转速搅拌摩擦焊接工艺优化[J]. 焊接, 2022(2): 32 − 38. Zhou Haibo, Pu Juan, Long Weimin, et al. Optimization of friction stir welding process for high-silicon aluminum alloy with ultra-high rotating speed based on Taguchi method[J]. Welding& Joining, 2022(2): 32 − 38.
[9]	高祎晗, 国旭明, 莫春立. 铝合金无减薄搅拌摩擦焊工艺优化及特征分析[J]. 焊接学报, 2019, 40(4): 141 − 147. doi: 10.12073/j.hjxb.2019400115 Gao Yihan, Guo Xuming, Mo Chunli. Process optimization and characteristics analysis of aluminum alloy friction stir welding without thinning[J]. Transactions of the China Welding Institution, 2019, 40(4): 141 − 147. doi: 10.12073/j.hjxb.2019400115
[10]	赵丹丹, 焦锋. 基于灰色关联分析的35CrMoV钢活塞杆激光熔覆工艺参数优化[J]. 兵工学报, 2018, 39(10): 2073 − 2080. doi: 10.3969/j.issn.1000-1093.2018.10.022 Zhao Dandan, Jiao Feng. Optimization of laser melting process parameters of 35CrMoV steel piston rod based on grey correlation analysis[J]. Acta Armamentarii, 2018, 39(10): 2073 − 2080. doi: 10.3969/j.issn.1000-1093.2018.10.022
[11]	王敬敏, 郭继伟, 连向军. 两种改进的灰色关联分析法的比较研究[J]. 华北电力大学学报, 2005, 32(6): 72 − 76. Wang Jingmin, Guo Jiwei, Lian Xiangjun. Comparative study of two improved grey correlation analysis methods[J]. Journal of North Electric Power University, 2005, 32(6): 72 − 76.
[12]	杨来侠, 桂玉莲, 李素丽, 等. 信噪比与灰色关联分析选区激光烧结成型工艺的研究[J]. 塑料工业, 2020, 48(1): 78 − 81. doi: 10.3969/j.issn.1005-5770.2020.01.017 Yang Laixia, Gui Yulian, Li Suli, et al. Signal noise ratio and gray correlation analysis of selective laser sintering molding process[J]. Plastic Industry, 2020, 48(1): 78 − 81. doi: 10.3969/j.issn.1005-5770.2020.01.017
[13]	Pitchipoo P, Muthiah A, Jeyakumar K, et al. Friction stir welding parameter optimization using novel multi objective dragonfly algorithm[J]. International Journal of Lightweight Materials and Manufacture, 2021, 4(4): 460 − 467. doi: 10.1016/j.ijlmm.2021.06.006
[14]	Shunmugasundaram M, Kumar P A, Sankar P L, et al. Optimization of process parameters of friction stir welded dissimilar AA6063 and AA5052 aluminum alloys by Taguchi technique[J]. Materials Today:Proceedings, 2020, 27(2): 871 − 876.
[15]	张先炼, 何晓聪, 程强, 等. 1420铝锂合金自冲铆异质组合接头静力学性能研究[J]. 材料导报, 2015, 29(24): 76 − 79. Zhang Xianlian, He Xiaocong, Cheng Qiang, et al. Study of the static mechanical properties of 1420 aluminum-lithium alloy self-piercing riveted heterogeneous composite joints[J]. Materials Reports, 2015, 29(24): 76 − 79.
[16]	Lei L, He X C, Xing B Y, et al. Effect of foam copper interlayer on the mechanical properties and fretting wear of sandwich clinched joints[J]. Journal of Materials Processing Tech, 2019, 274: 116285. doi: 10.1016/j.jmatprotec.2019.116285
[17]	Anbarasi J, Yaknesh S, Sampathkumar K, et al. Performance characteristics optimization in dissimilar friction stir welding using Grey relational analysis[J]. Materials Today:Proceedings, 2022, 55(2): 294 − 298.
[18]	Mostafa A, Parviz A. Optimization of microstructural and mechanical properties of friction stir welded A356 pipes using Taguchi method[J]. Materials Research Express, 2019, 6(6): 066545. doi: 10.1088/2053-1591/ab0d72
[19]	王排岗, 王晓强, 刘志飞, 等. 基于灰色关联分析方法的超声滚挤压工艺参数优化[J]. 塑性工程学报, 2022, 29(3): 36 − 43. doi: 10.3969/j.issn.1007-2012.2022.03.005 Wang Paigang, Wang Xiaoqiang, Liu Zhifei, et al. Optimization of ultrasonic rolling extrusion process parameters based on grey correlation analysis method[J]. Chinese Journal of Plastic Engineering, 2022, 29(3): 36 − 43. doi: 10.3969/j.issn.1007-2012.2022.03.005
[20]	梁存光, 李新梅. 基于灰色关联分析与回归分析WC-12Co涂层工艺参数的多目标优化[J]. 材料导报, 2018, 32(10): 1752 − 1756. doi: 10.11896/j.issn.1005-023X.2018.10.034 Liang Cunguang, Li Xinmei. Multi-objective optimization of WC-12Co coating process parameters based on grey correlation analysis and regression analysis[J]. Materials Reports, 2018, 32(10): 1752 − 1756. doi: 10.11896/j.issn.1005-023X.2018.10.034
[21]	苏孺, 王朋朋, 张亮. 主轴转速对2A12铝合金搅拌摩擦焊接头组织和性能的影响[J]. 沈阳大学学报, 2019, 31(6): 443 − 447. Su Ru, Wang Pengpeng, Zhang Liang. Effect of spindle speed on microstructure and properties of friction stir welding joint of 2A12 aluminum alloy[J]. Journal of Shenyang University, 2019, 31(6): 443 − 447.
[22]	朱海, 于明玉, 郭春成, 等. 6061-T6铝合金无针搅拌摩擦焊全焊缝力学性能研究[J]. 塑性工程学报, 2021, 28(12): 97 − 102. doi: 10.3969/j.issn.1007-2012.2021.12.012 Zhu Hai, Yu Mingyu, Guo Chuncheng, et al. Research on mechanical properties of 6061-T6 aluminum alloy friction stir welding without pin[J]. Chinese Journal of Plastic Engineering, 2021, 28(12): 97 − 102. doi: 10.3969/j.issn.1007-2012.2021.12.012
[23]	郭柱, 朱浩, 崔少朋, 等. 7075铝合金搅拌摩擦焊接头温度场及残余应力场的有限元模拟[J]. 焊接学报, 2015, 36(2): 92 − 96. Guo Zhu, Zhu Hao, Cui Shaopeng, et al. Finite element simulation of temperature field and residual stress field of 7075 aluminum alloy friction stir welding joint[J]. Transactions of the China Welding Institution, 2015, 36(2): 92 − 96.

施引文献(12)

期刊类型引用(7)

1.	胡高斌，钱勇武，钟治琨，彭浩，薛泳泳，陆伟. 汽轮机用铝/钢接头MAO层结构和腐蚀性能分析. 电镀与精饰. 2023(01): 33-38 . 百度学术
2.	韩善果，杨永强，罗子艺，蔡得涛，郑世达. 线能量对铝/钢双光束激光焊接接头组织及性能的影响. 材料导报. 2021(02): 2109-2114 . 百度学术
3.	杨扬，周信，于霜，柏余杰，吕亚男. 不同坡口面角度镀锌钢/铝合金激光熔钎焊接头的界面组织和拉伸性能. 机械工程材料. 2021(12): 55-61 . 百度学术
4.	贾剑平，詹志平. 铝钢熔钎焊工艺及腐蚀性能研究进展. 热加工工艺. 2020(11): 1-5 . 百度学术
5.	周丹，李翠，易鑫，叶兵，李斌. 送丝速度对铝/钢激光填丝熔钎焊性能的影响. 焊接. 2019(03): 38-43+67 . 百度学术
6.	薛松柏，王博，张亮，龙伟民. 中国近十年绿色焊接技术研究进展. 材料导报. 2019(17): 2813-2830 . 百度学术
7.	李杰，黄健康，靳全胜. 铝/钢异种金属熔钎焊方法研究现状. 电焊机. 2018(01): 109-114 . 百度学术