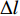-
承压设备广泛应用在石化、核电等领域，常采用焊接方法制造，但在焊接过程中不可避免产生焊接残余应力[1]，对应力腐蚀开裂(SCC)、蠕变和疲劳失效影响很大[2-5]. 因此需要采用热处理消除焊接残余应力[6]. 近10年，国内实施了“千万吨炼油、百万吨乙烯”和“百万千万核电”国家战略，迫使承压设备向大型化发展[7]. 如核电钢制安全壳直径突破43 m，石化加氢反应器壁厚达352 mm. 由于受体积限制，不能整体热处理，只能采用分段焊接、分段热处理、整体组装的方法进行制造. 而整体组装过程中会产生合拢总装焊缝，只能进行局部热处理[8].
实践证明，采用现有局部热处理方法和标准，大量焊缝依然产生应力腐蚀开裂[9,10]，引起国内外学者的广泛关注. Kang等人[11]对韩国YGU3号压水堆封头与通风管连接焊缝的开裂事故进行应力分析和失效调查，发现引起应力腐蚀开裂的主要原因是在焊缝内表面附近存在较大的拉伸残余应力. 王泽军等人[12]研究了加氢反应器不同局部热处理工艺下的应力分布，发现热处理后内壁焊缝残余应力无法得到有效消除，但未对该原因展开深入研究. 汪建华等人[13]分析了不同加热带宽度对局部热处理消应力效果的影响，提出了
$ {\text{5}}\sqrt {Rt} $ 的加热带宽度用于消除残余应力，这与标准PD 5500:2015[14]和EN 13445-4:2009[15]建议的最小加热带宽度一致. 但采用这一方法，对于大型压力容器，加热带宽度过大. 如直径为6 m、壁厚为300 mm的压力容器，需要的加热带宽度达9 m，无法现场实施. 陆皓等人[16]通过黏弹塑性有限元法对管道局部热处理应力分布展开研究，发现外壁应力随加热带宽度增加缓慢下降，加热带宽度增加对内壁应力释放作用不大. 国家标准GB/T 30583—2014《承压设备焊后热处理规程》[17]规定，设备的厚度δ ≤ 50 mm时，加热带宽度HB = 7nhk(1＜n ＜ 3，hk为焊缝最大宽度，n如何确定未给出依据)，对于δ ＞ 50 mm的设备没有给出明确的规定. 但随着当前千万吨炼油技术的发展，国内重型承压设备壁厚已普遍超过50 mm，目前国内外方法均无法解决这一行业难题，亟需研究新的理论和技术[18].文章对局部热处理后残余应力进行大量计算和测试表明传统单加热带局部热处理方法无法消除焊缝内表面残余应力，并揭示无法消除的原因，在此基础上，提出一种主副加热分布式热源局部热处理新方法. Houman[19]、Liu[20]等人认为该方法可以显著降低焊接残余应力，能够在容器焊缝内表面产生一定的压应力，Berto[21]、Song[22]等人称其为“蒋氏热处理方法”.
-
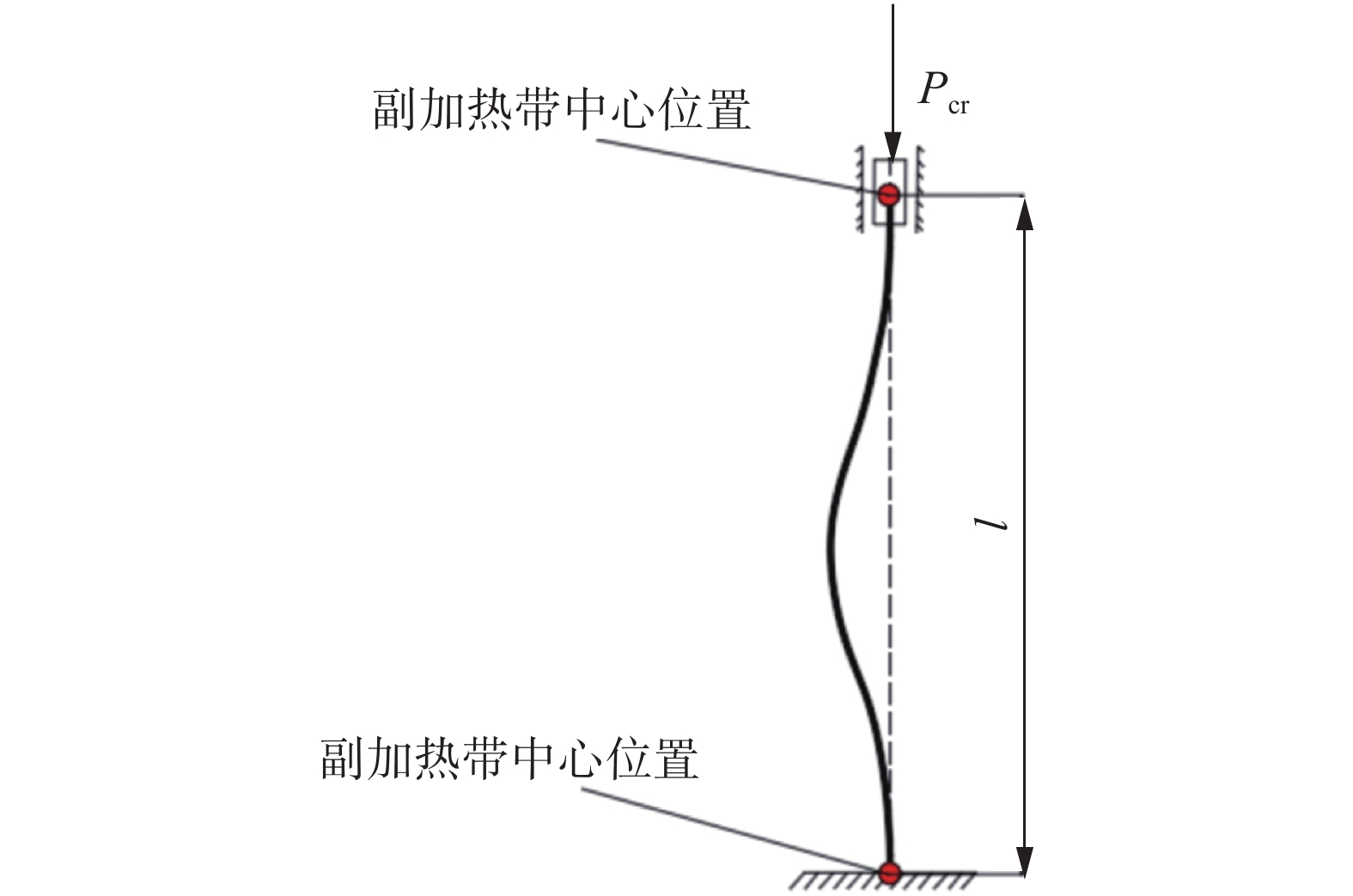
主副加热局部热处理是在传统单加热带基础上，距离焊缝一定位置施加副加热区，如图1所示. 主加热区施加在焊缝，调控微观组织、力学性能，关键工艺参数应结合技术设计文件和相关标准确定，主要包括加热和冷却速率、保温温度和时间、主加热带宽度(WPHB). 副加热区布置在焊缝两侧距离焊缝中心一定距离，用于调控内表面残余应力，关键工艺参数包括副加热带中心位置到焊缝中心距离(WDCB)、副加热带最高温度(TA)、副加热带宽度(WAHB). 当主加热温度降至室温后对副加热进行升温.
图 1 加热带布置示意图
Figure 1. Diagram of heating belt layout
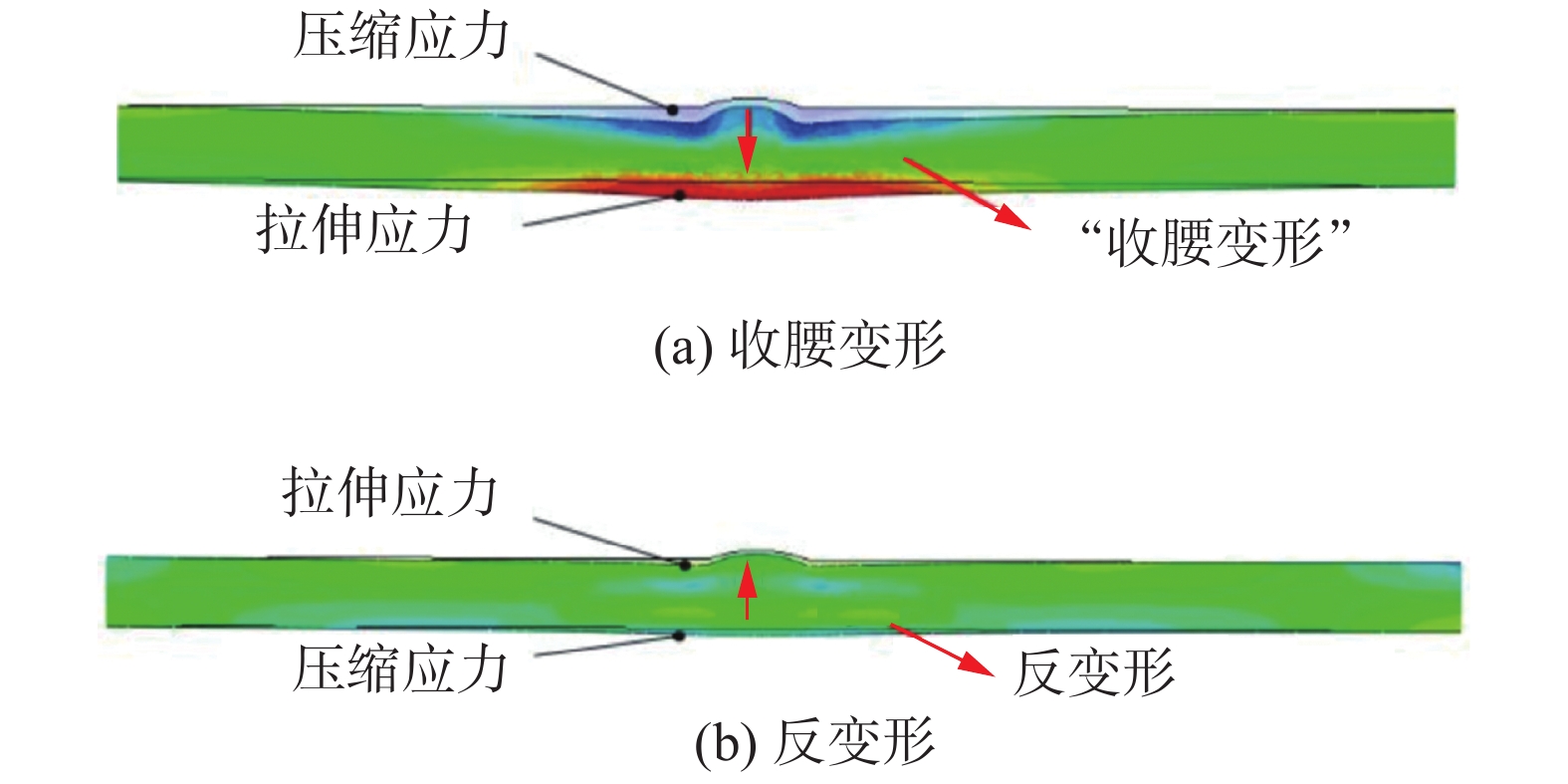
采用单一热源加热时，加热区向外膨胀，焊缝附近应力分布为外拉内压. 随后，加热区随着温度的降低逐渐开始收缩，当温度降至室温时，出现“收腰”变形，应力分布表现为外压内拉，这种收腰变形会在内表面焊缝附近产生二次拉伸应力，如图2a所示. 主副加热分布式热源通过在焊缝一定距离施加副加热，与焊缝形成温度梯度，产生反变形，抵消主加热产生的“收腰变形”，消除焊缝内表面残余应力，如图2b所示. 主副加热带的温度均可局部调节，满足热处理温度均匀性及应力调控需求.
图 2 应力消除机理
Figure 2. Stress relief mechanism. (a) waist deformation; (b) reverse deformation
-
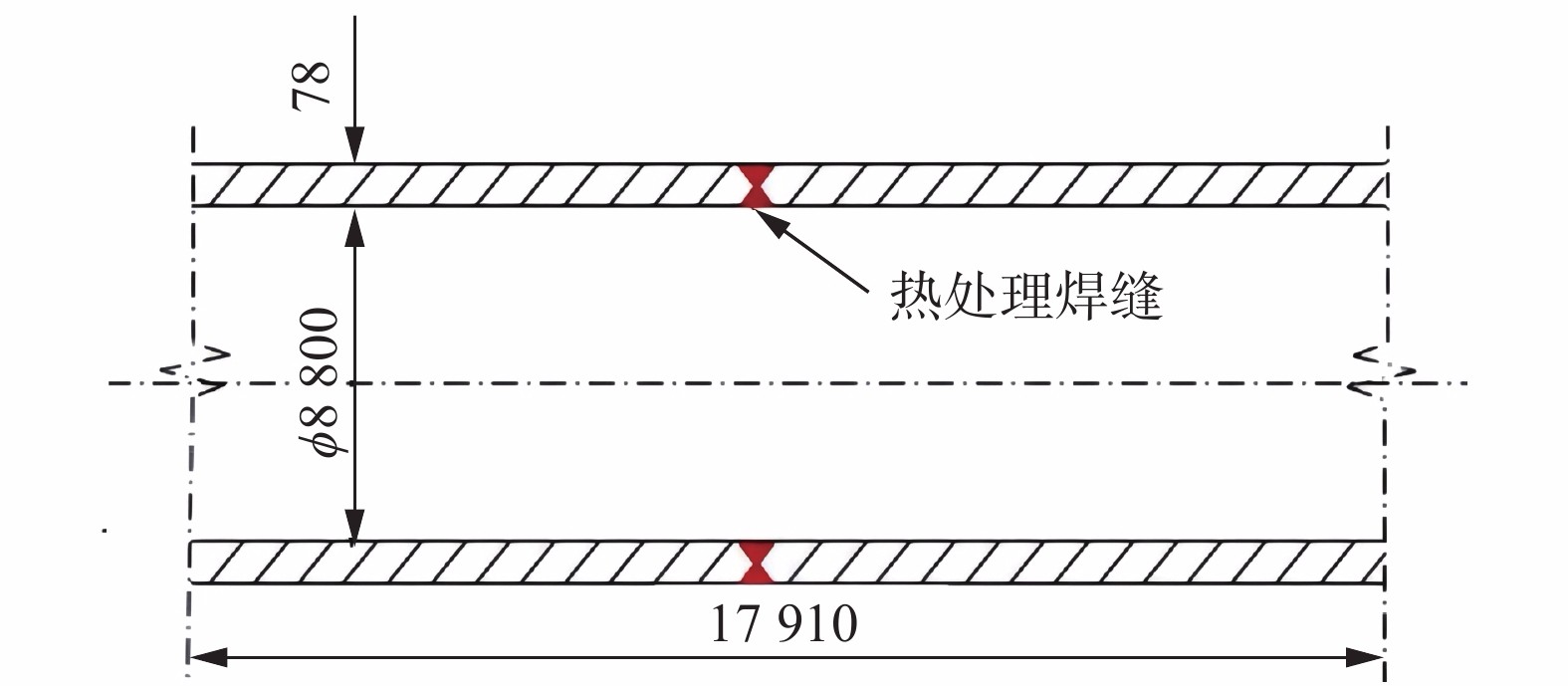
以某二甲苯塔为研究对象，塔体总长为113 m，无法整体热处理，只能分段制造、分段热处理，然后对总装焊缝进行局部热处理. 其中一节分段筒节尺寸如图3所示，采用X形坡口焊接，内侧坡口角度为50°，外侧坡口角度为60°. 焊接方法为熔化极气体保护焊 (GMAW)，电弧电压为22 ~ 30 V，焊接电流为160 ~ 220 A，焊接速度为10 ~ 30 cm/min. 焊道间温度控制在250 ℃以下，最低预热温度为80 ℃.
图 3 试验对象尺寸
Figure 3. Test object size
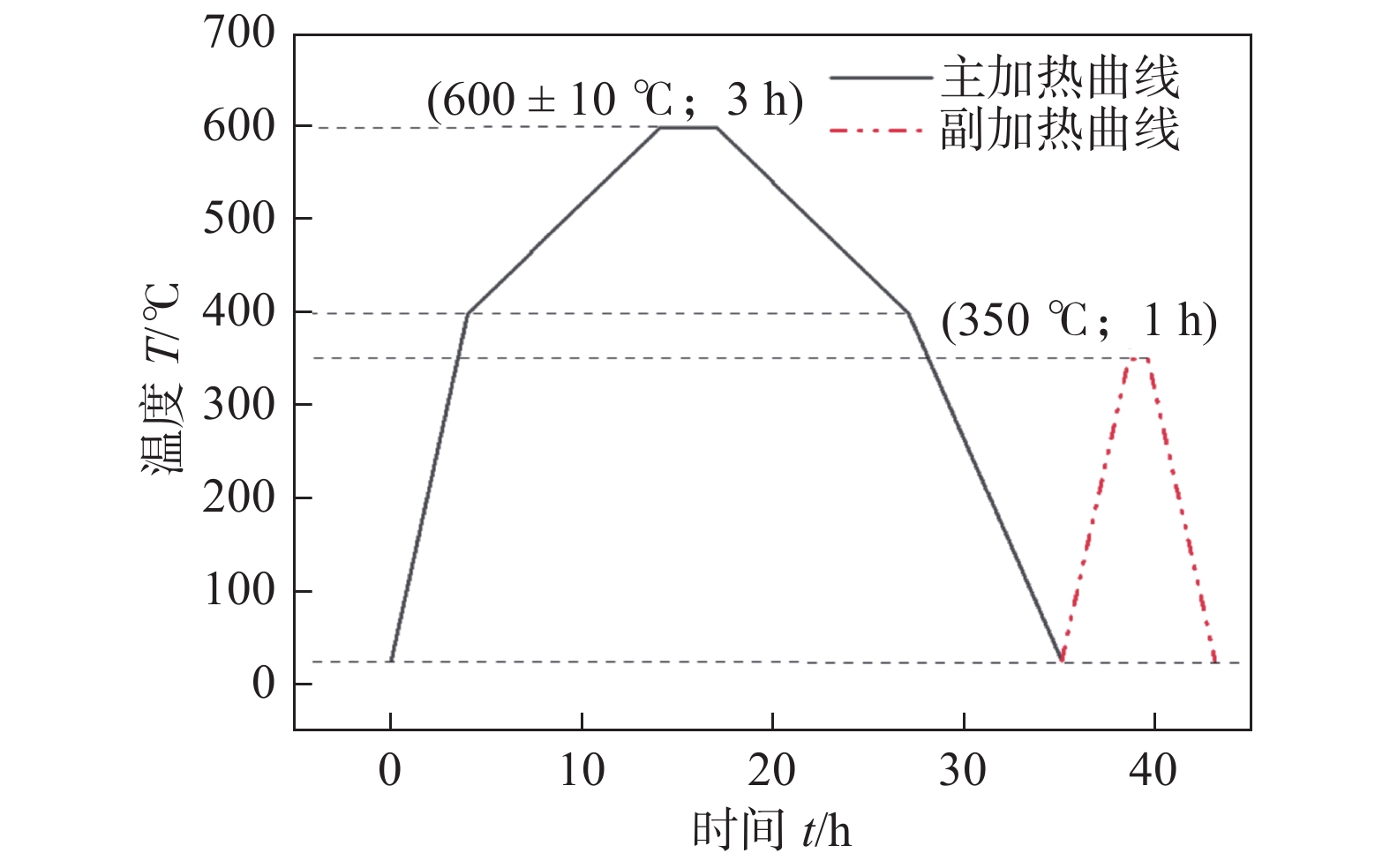
图4给出了合拢焊缝主副加热局部热处理工艺曲线. 主加热宽度为500 mm，将主加热升温至600 ℃，保温2 h，并用热电偶记录热处理过程内外壁温度分布. 保温结束后，当温度低于400 ℃时，筒体自然冷却. 主加热温度降至室温时，施加副加热，副加热最高温度为350 ℃、副加热带宽度为 300 mm，主副加热间距为1 400 mm，主副加热局部热处理现场如图5所示.
图 4 局部热处理工艺曲线
Figure 4. Local heat treatment curve
图 5 现场试验
Figure 5. Field experiment
采用压痕法[23]测试筒体内表面热处理前后残余应力. 基本原理是将电阻应变片作为测量应变的敏感元件，利用球形压头在应变栅轴线中心点施加机械载荷诱导产生应变增量，并用应变仪进行记录. 利用预先标定的弹性应变
${\varepsilon _{\text{e}}}$ 与应变增量$ \Delta \varepsilon $ 之间的关系得到残余应变，残余应力σx，σy可由胡克定律计算求得.$$ \sigma_{x}=\frac{E}{1-\upsilon^{2}}\left(\varepsilon_{x} + \upsilon \varepsilon_{y}\right) $$ (1) $$ \sigma_{y}=\frac{E}{1-\upsilon^{2}}\left(\varepsilon_{y} + v \varepsilon_{x}\right) $$ (2) 式中：E为弹性模量；
$\upsilon $ 为泊松比；${\varepsilon _x}$ ，${\varepsilon _y}$ 为残余弹性应变分量.测试路径垂直焊缝，测点包括焊缝、热影响区及母材.
-
采用顺次耦合方法计算焊接残余应力，为节省篇幅，不进行详细介绍，详见文献[18]. 建立了与实际分段筒节尺寸完全一致的有限元模型. 有限元模型及网格划分如图6所示. 为兼顾计算精度与时间，在焊缝及热影响区附近网格划分较密，远离焊缝区域较稀疏，温度场计算采用DCAX4单元，应力场计算采用CAX4H单元，热分析和力分析使用相同的单元和节点. 材料参数见表1.
图 6 有限元模型及网格划分
Figure 6. Finite element model and meshing
表 1 Q345R材料参数
Table 1. Material parameters of Q345R
温度T/℃ 弹性模量E/GPa 屈服强度ReL/MPa 泊松比ν 热膨胀系数α/(10−6 K−1) 导热系数λ/(W·m−1·K−1) 比热容c/(J·kg−1·K−1) 20 210 345 0.3 7.3 53.2 461 200 201 317 0.3 11.0 47.7 523 400 185 267 0.3 13.2 39.6 607 600 160 160 0.3 13.9 36.0 678 800 145 120 0.3 14.0 33.0 700 采用内生热源模拟焊接过程，内生热率等于电弧有效功率与所作用单元体积的比值，热流密度q计算公式[24]为
$$ q = \eta UI/(Sv) $$ (3) 式中：
$ \eta $ 为电弧热效率；U为电弧电压；I为焊接电流；S为焊缝截面积；v为焊接速度.在热处理模拟中，加热区和保温区域强制对流换热系数为6 × 106 W/(m2∙K)，按图4所示的热处理曲线创建幅值曲线进行升温和保温，加热区以外对流换热系数为10 W/(m2∙K)，辐射系数为0. 85，初始温度取20 ℃. 在应力场分析时，约束筒体端部的位移，防止刚体移动.
-
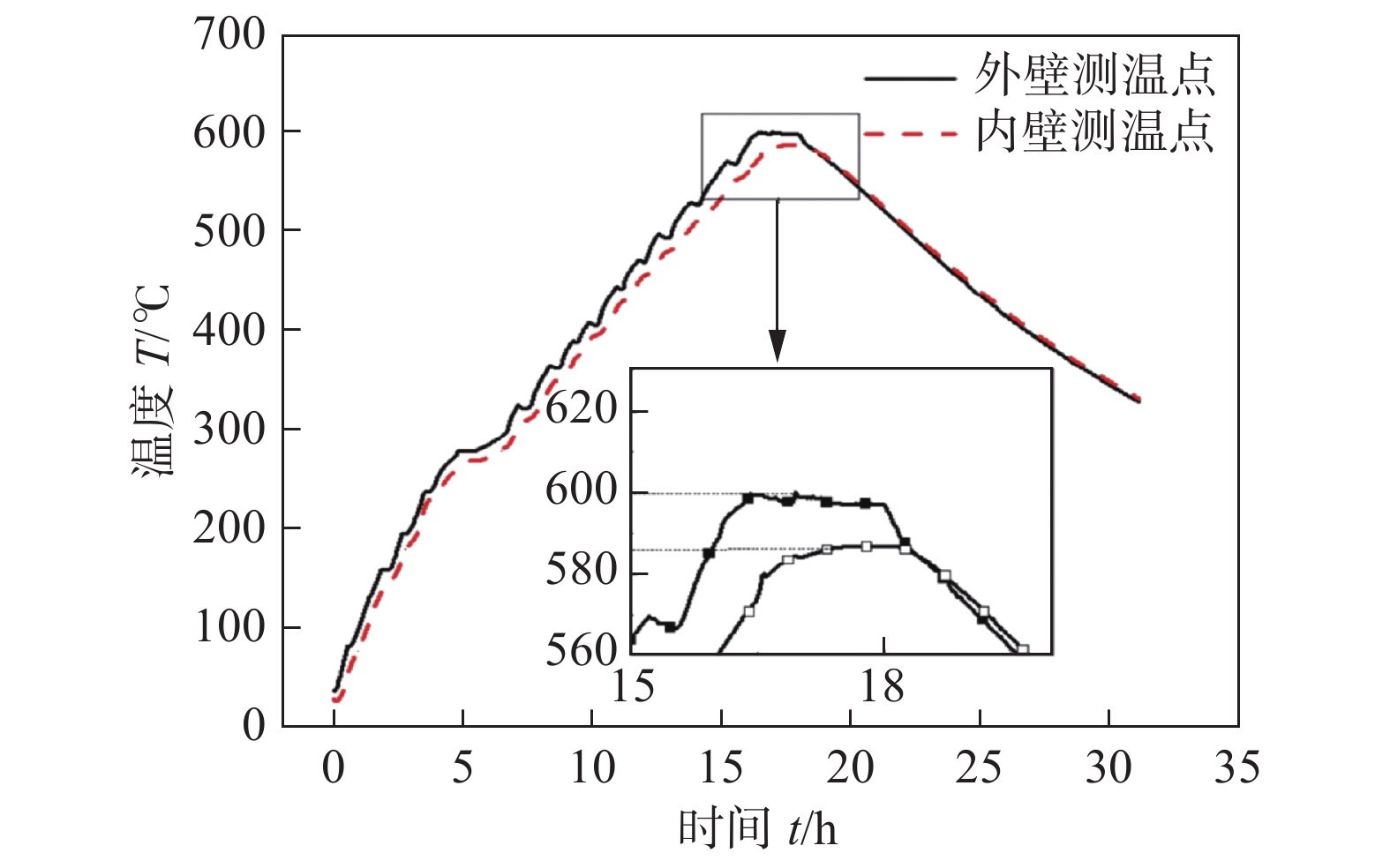
图7和图8分别给出了主加热过程热电偶测温及有限元模拟结果. 保温时刻，试验测试结果内外表面最大温差为17 ℃，有限元模拟为16 ℃，说明温度场模拟方法正确.
图 7 热电偶测温结果
Figure 7. Thermocouple temperature measurement result
图 8 温度场分布云图
Figure 8. Temperature contours at holding time
图9，图10分别为焊态、传统热处理和主副加热方式下的残余应力分布云图. 焊态轴向应力最大值位于内表面焊趾附近，为318 MPa. 传统局部热处理后，内壁焊缝附近应力分布为外压内拉，相对焊态略有升高，最大值为335 MPa. 采用主副加热局部热处理方法，焊缝内表面应力明显降低，最大值仅为87 MPa，分布均匀. 焊态环向应力最大值位于焊趾处，为345 MPa. 传统热处理方法后，以外表面为起点沿厚度方向1/2区域应力水平有所改善，其余位置仍表现为较大的拉应力. 主副加热后，环向应力明显降低，沿厚度方向分布均匀，最大值为137 MPa.
图 9 轴向应力分布
Figure 9. The contour distribution of axial residual stress.(a) as-welded; (b) traditional method; (c) primary and secondary distributed heat source method
图 10 环向应力分布
Figure 10. The contour distribution of hoop residual stress. (a) as-welded; (b) traditional method; (c) primary and secondary distributed heat source method
图11给出了沿内表面路径P1的残余应力分布规律. 数值模拟得到的应力分布与试验结果基本吻合. 结果表明，传统热处理产生收腰变形，母材位置引入了新的热应力和弯曲应力，导致应力明显升高. 焊缝处沿分析路径P1，垂直于焊缝方向的轴向应力不降反升，最大值由318 MPa增长至334 MPa. 沿焊缝方向的环向应力最大值由345 MPa降至306 MPa，降低了11%. 这是由于焊接接头受热膨胀，冷却产生周向收缩，产生剪切力和弯矩. 弯矩使轴向应力增大，剪应力使环向应力减小. 副加热后，产生反变形，使焊缝处轴向应力最大值由318 MPa降到87 MPa，环向应力最大值由345 MPa降到137 MPa，最大降幅分别为72.6%和60.3%，应力消除效果显著.
图 11 沿路径P1残余应力分布
Figure 11. Residual stress distribution along path P1. (a) axial stress; (b) hoop stress
-
图12给出了副加热带宽度为300 mm、主副加热间距为900 mm的不同副加热温度对残余应力的影响. 随着副加热温度的升高，残余应力消除效果增加，当副加热温度从200 ℃增加至600 ℃，轴向应力降幅由130.2%增至174.8%，提高44.6%. 环向应力降幅由118.3%增至145.9%，降幅提高 27.6%. 这是由于温度升高，副加热产生更大反变形，对焊缝处收腰变形协调效果增加，应力降低更加明显.
图 12 沿路径P1残余应力分布
Figure 12. Residual stress distribution along path P1. (a) axial stress; (b) hoop stress
-
图13给出了副加热温度为350 ℃、主副加热间距为900 mm的不同副加热带宽度下沿P1路径应力分布. 可见，副加热宽度由200 mm增加至500 mm，轴向应力消除效果增加25%，环向应力消除效果增加10. 9%. 这是由于在副加热带位置处产生更大的变形驱动力，焊缝处产生更大的反变形，降低应力. 值得注意的是，当宽度增加至700 mm后的应力降幅比500 mm减少，由此可见，当副加热带宽度过宽时，由于轴向传热的影响，焊缝位置在副加热保温过程产生周向膨胀，一定程度抵消副加热带的反变形作用，从而应力消除效果降低.
图 13 沿路径P1残余应力分布
Figure 13. Residual stress distribution along path P1. (a) axial stress; (b) hoop stress
-
图14给出了副加热带宽度为300 mm、副加热温度为350 ℃的主副加热间距对应力消除效果的影响. 当间距由1 400 mm减小至900 mm时，轴向应力降幅增加79.9%，环向降幅增加66.5%，产生压应力，而1 400 mm仍表现为一定程度的拉应力. 这是因为主副加热间距决定着副加热产生的反变形是否作用于焊缝处，是内壁应力调控效果的主导因素.
图 14 沿路径P1残余应力分布
Figure 14. Residual stress distribution along path P1. (a) axial stress; (b) hoop stress
-
主加热带宽度(WPHB)是保证均温区温度均匀性的关键参数，图15给出了上述二甲苯塔不同主加热宽度均温区保温时刻内表面温度分布. 主加热宽度为2t(t为加热区壁厚)，4t，5t时，均温区边缘温度小于所允许的最低温度580 ℃，无法满足均温要求. 主加热宽度增加至6t和8t时，均温区最低温度分别为584和588 ℃，符合工艺要求，且宽度继续增加对均温区温度影响不大. 通过大量试验研究和计算，综合考虑温度均匀性和现场操作要求，提出主加热带宽度应满足以下公式，即
图 15 内壁均温区温度分布
Figure 15. Temperature distribution of inner surface
$$ W_{\mathrm{PHB}}=(6 \sim 8) t $$ (4) 由图12可知，副加热最高温度TA为主加热区保温温度的40% ~ 60%即可产生较好的应力消除效果. 图13表明，合理选择副加热带宽度能够获得较好的应力消除效果，最佳副加热宽度应满足以下公式，即
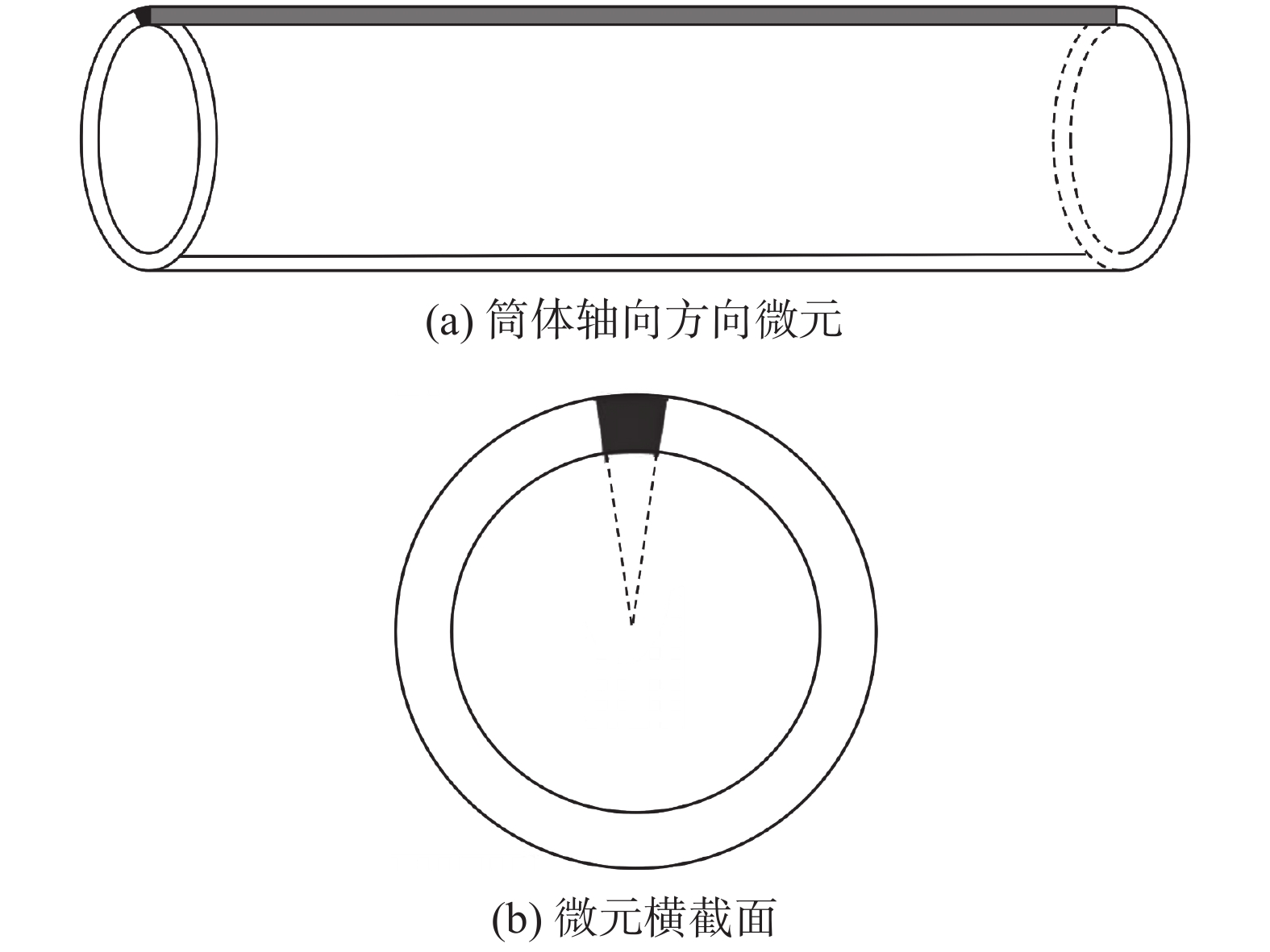
$$ W_{\mathrm{AHB}}=(3 \sim 4) t$$ (5) 主副加热间距是应力消除效果的关键因素，为便于该方法的工程应用，从理论角度推导最优主副加热间距计算公式. 沿筒体轴向在管道上部取一个微元. 所取微元为灰色阴影部分，微元横截面形状为扇形的一部分，如图16所示.
图 16 微元模型
Figure 16. Infinitesimal element selection method. (a) cylinder axial infinitesimal element; (b) infinitesimal element cross section
假设副加热带的温度均匀. 副加热带对应的加热区受到相邻低温筒体的约束无法自由伸长且无法弯曲变形，副加热区在最高温度时本应该产生
$\Delta l{\text{ = }}\alpha l\Delta T$ 即被完全限制，相应于这种限制，副加热区内产生了压缩应力. 即副加热区受热后本应比受热前伸长$ \Delta l $ ，由于受到约束和限制，副加热区受热后的长度仍为l，相当于副加热区受热后受到一轴向应力P，长度为$ l + \Delta l $ 的副加热区产生了轴向压缩变形$ \Delta l $ . 如果压缩变形全是弹性变形，则有$$ \Delta l = \frac{{Pl}}{{EA}} $$ (6) 式中：l为两个副加热带中心之间的距离；E为副加热带升高至最高温度时材料的弹性模量；A为所取微元横截面积.
当所取微元受到两端副加热带的热应力作用时，受筒体其他部分的约束作用，无法自由伸长，微元内部即出现了压缩载荷，则有
$$ 2\alpha {W_{{\text{AHB}}}}\Delta T = \frac{{Pl}}{{EA}} $$ (7) 则内部压缩载荷大小为
$$ P = \frac{{2\alpha {W_{{\text{AHB}}}}\Delta TEA}}{l} $$ (8) 式中：
$ \alpha $ 为副加热升至最高温度下的热膨胀系数；WAHB为副加热带宽度；$ \Delta T $ 为副加热最高温度与室温的温度差.由于图16所取微元的轴向长度远大于其截面尺寸，故可将该模型看作细长杆，副加热带引起的筒体变形，可简化为图17所示的屈曲变形问题. 此时可以认为，当两个副加热带之间距离合适时，其产生的轴向压缩载荷与压杆屈曲的临界载荷相等，从而发生屈曲变形，并与主加热产生的变形抵消，内表面即可产生压缩应力，此时主副加热局部热处理效果最佳.
图 17 压杆失稳模型
Figure 17. Compression rod instability model
图17所示的屈曲变形问题可通过压杆失稳的相关理论得到其临界压缩载荷，即
$$ {P_{cr}} = \frac{{n{{\text{π }}^2}EI}}{{{{(\mu l)}^2}}} $$ (9) 式中，Pcr为临界压缩载荷；E为副加热升至最高温度下的弹性模量；I对形心主惯性轴的惯性矩；l为两个副加热带间距；n取1；µ取0. 5.
令式(8)与式(9)相等，即P = Pcr，可得
$$ \frac{{2\alpha {W_{{\text{AHB}}}}\Delta TEA}}{l}{\text{ = }}\frac{{4{{\text{π }}^2}EI}}{{{l^2}}} $$ (10) 化简式(10)可得两个副加热带之间的距离为
$$ l = \frac{{2{\text{π } ^2}}}{{\alpha {W_{{\text{AHB}}}}\Delta T}} \cdot \frac{I}{A} = \frac{{2{{\text{π }}^2}{i^2}}}{{\alpha {W_{{\text{AHB}}}}\Delta T}} $$ (11) 式中：i为压杆横截面对形心主惯性轴的惯性半径，i的取值与压杆的截面形状有关.
所取微元截面形状是扇形的一部分，但当取的微元足够小时，其截面形状将无限接近于矩形，如图18所示，矩形截面的高与管道的厚度t相等.
图 18 简化模型的截面形状
Figure 18. Cross-section shape of the simplified model
则惯性半径i为
$$ i = \sqrt {\frac{{{I_y}}}{A}} = \sqrt {\frac{{b{t^3}}}{{{\text{12}}}}/bt} = \frac{t}{{\sqrt {{\text{12}}} }} $$ (12) 将式(12)代入式(11)，即可得主副加热带间距为两副加热带间距的1/2，表示为
$$ {W_{{\text{DCB}}}} = \frac{l}{2}{\text{ = }}\frac{{2{{\text{π }}^2}{i^2}}}{{\alpha {W_{{\text{AHB}}}}\Delta T}}{\text{ = }}\frac{{{{\text{π }}^2}{t^2}}}{{12\alpha {W_{{\text{AHB}}}}\Delta T}} $$ (13) 已知WAHB = (3 ~ 4)·t，取WAHB = 3t，则式(13)可表示为
$$ {W_{{\text{DCB}}}}{\text{ = }}\frac{{{{\text{π }}^2}t}}{{36\alpha \Delta T}} $$ (14) 主副加热间距是应力调控效果的关键影响参数，且其值受直径的影响较大，公式(14)未考虑直径的影响，使得公式计算值和有限元模拟值有差异. 为了使公式计算值更接近有限元模拟值，通过引入修正系数η对公式(14)进行修正，修正后的公式为：
$$ {W_{{\text{DCB}}}} = \eta \frac{{{{\text{π }}^2}t}}{{36\alpha \Delta T}} $$ (15) 通过大量的有限元计算，图19给出了Q345R不同直径、壁厚下的修正系数η. 对于同一壁厚，随着直径增大，修正系数η增大. 壁厚越小，修正系数η增加越快. 壁厚越大，修正系数η增加越缓慢. 对于同一直径，随着壁厚增大，修正系数η减小.
图 19 修正系数η
Figure 19. Correction coefficient η
以内径为12 000 mm，壁厚为100 mm筒体为例，式(15)计算的主副加热间距为1 312 mm，有限元模拟值为1 326 mm. 计算值和模拟值相差较小，验证了公式的正确性.
-
(1) 传统单加热局部热处理方法冷却后，焊缝收缩产生“收腰变形”，在内表面产生新的二次拉伸残余应力，导致焊接接头内表面的残余应力降低不明显甚至增加. 采用主副加热局部热处理方法，能够利用副加热区的反变形，抵消“收腰变形”，显著消除残余应力.
(2) 主副加热局部热处理方法能够使局部热处理效果达到最优，应力消除效果受副加热参数影响较大，其中主副加热间距是应力消除效果的关键因素.
(3) 建立了主副加热局部热处理设计准则：主副加热间距的理论公式：
${W_{{\text{DCB}}}} = \eta \dfrac{{{{\text{π }}^2}t}}{{36\alpha \Delta T}}$ ，主加热区宽度WPHB = (6 ~ 8)t，副加热带宽度WAHB = (3 ~ 4)t.
Local Post Weld Heat Treatment Method by Primary and Secondary Distributed Heat Source
-
摘要: 局部热处理是保证承压设备全寿命周期安全性的重要手段. 文中以某二甲苯塔分段筒节为研究对象，提出了一种主副加热分布式热源局部热处理方法，在传统单加热基础上，距离焊缝一定位置施加副加热区，主加热用于改善焊缝微观组织、消除部分残余应力，副加热在焊缝产生反变形，抵消主加热产生的“收腰变形”，消除焊缝内表面残余应力. 采用试验、数值模拟和理论分析，建立了主副加热局部热处理有限元模型，研究了副加热带温度、宽度、主副加热间距对应力消除效果的影响规律. 结果表明，采用传统单加热热处理方法，降温阶段，焊缝受到拘束作用在内表面产生新的二次应力. 主副加热分布式热源局部热处理利用副加热区的反变形，可以在焊缝内表面产生压应力. 主副加热带宽度、间距和副加热温度是应力消除效果的关键因素，提出了主副加热局部热处理工程设计方法，为重大承压设备局部热处理提供依据.Abstract: Local heat treatment is an important means to ensure the safety of the whole life cycle of pressure-bearing equipment. This paper takes xylene tower segmented barrel as research subject and proposes a novel heat treatment method by adding a secondary heating band at certain distance from the primary heat source. The primary heating band improves the microstructure of the weld and the secondary heating band eliminates residual stresses on the internal surface of the weld and neutralizes the waist-closing deformation. This research established a local heat treatment model for primary and secondary heating, factors influencing the stress relief are investigated including the effects of the temperature, band-width of the secondary heating band, the spacing between the primary and secondary heating and et al. Results show that the traditional local heat treatment produces new secondary stresses on the inner surface due to the constraint effect. Primary and secondary heating distributed heat source local heat treatment can produce compressive stress on the inner surface of the weld due to the reversible deformation. The width and spacing of the primary and the secondary heating bands are crucial to stress relief and the engineering design methodology are proposed,which cast light on the heat treatment of extremely large sized pressure equipment.
-
图 2 应力消除机理
Figure 2. Stress relief mechanism. (a) waist deformation; (b) reverse deformation
图 9 轴向应力分布
Figure 9. The contour distribution of axial residual stress.(a) as-welded; (b) traditional method; (c) primary and secondary distributed heat source method
图 10 环向应力分布
Figure 10. The contour distribution of hoop residual stress. (a) as-welded; (b) traditional method; (c) primary and secondary distributed heat source method
图 11 沿路径P1残余应力分布
Figure 11. Residual stress distribution along path P1. (a) axial stress; (b) hoop stress
图 12 沿路径P1残余应力分布
Figure 12. Residual stress distribution along path P1. (a) axial stress; (b) hoop stress
图 13 沿路径P1残余应力分布
Figure 13. Residual stress distribution along path P1. (a) axial stress; (b) hoop stress
图 14 沿路径P1残余应力分布
Figure 14. Residual stress distribution along path P1. (a) axial stress; (b) hoop stress
图 16 微元模型
Figure 16. Infinitesimal element selection method. (a) cylinder axial infinitesimal element; (b) infinitesimal element cross section
表 1 Q345R材料参数
Table 1. Material parameters of Q345R
温度T/℃ 弹性模量E/GPa 屈服强度ReL/MPa 泊松比ν 热膨胀系数α/(10−6 K−1) 导热系数λ/(W·m−1·K−1) 比热容c/(J·kg−1·K−1) 20 210 345 0.3 7.3 53.2 461 200 201 317 0.3 11.0 47.7 523 400 185 267 0.3 13.2 39.6 607 600 160 160 0.3 13.9 36.0 678 800 145 120 0.3 14.0 33.0 700 
下载: 导出CSV
-
[1] 游敏, 郑小玲, 余海洲. 关于焊接残余应力形成机制的探讨[J]. 焊接学报, 2003, 24(2): 51 − 54,58. doi: 10.3321/j.issn:0253-360X.2003.02.014 You Min, Zheng Xiaoling, Yu Haizhou. Discussion on forming mechanism of welding residual stress[J]. Transactions of the China Welding Institution, 2003, 24(2): 51 − 54,58. doi: 10.3321/j.issn:0253-360X.2003.02.014 [2] Yazdanpanah A, Franceschi M, Bergamo G, et al. On the exceptional stress corrosion cracking susceptibility of selective laser melted 316L stainless steel under the individual effect of surface residual stresses[J]. Engineering Failure Analysis, 2022, 136: 106192. doi: 10.1016/j.engfailanal.2022.106192 [3] 张国栋, 周昌玉. 焊接残余应力对焊接接头蠕变性能的影响[J]. 焊接学报, 2007, 28(8): 99 − 102,107. doi: 10.3321/j.issn:0253-360x.2007.08.026 Zhang Guodong, Zhou Changyu. Effect of welding residual stress on creep properties of welded joints[J]. Transactions of the China Welding Institution, 2007, 28(8): 99 − 102,107. doi: 10.3321/j.issn:0253-360x.2007.08.026 [4] Puliyaneth M, Chen H. Study on the effect of welding residual stress on creep-cyclic plasticity behaviour[J]. International Journal of Pressure Vessels and Piping, 2021, 193: 104444. doi: 10.1016/j.ijpvp.2021.104444 [5] Jiang W, Xie X, Wang T, et al. Fatigue life prediction of 316L stainless steel weld joint including the role of residual stress and its evolution: Experimental and modelling[J]. International Journal of Fatigue, 2021, 143: 105997. doi: 10.1016/j.ijfatigue.2020.105997 [6] Luo Y, Jiang W, Yang Z, et al. Using reinforce plate to control the residual stresses and deformation during local post-welding heat treatment for ultra-large pressure vessels[J]. International Journal of Pressure Vessels and Piping, 2021, 191: 104332. doi: 10.1016/j.ijpvp.2021.104332 [7] Jin Q, Jiang W, Wang C, et al. A rigid-flexible coordinated method to control weld residual stress and deformation during local PWHT for ultra-large pressure vessels[J]. International Journal of Pressure Vessels and Piping, 2021, 191: 104323. doi: 10.1016/j.ijpvp.2021.104323 [8] Liu M, Ni Z, Du C, et al. Failure investigation of a 304 stainless steel geothermal tube[J]. Engineering Failure Analysis, 2021, 129: 105694. doi: 10.1016/j.engfailanal.2021.105694 [9] Nyrkova L, Melnichuk S, Osadchuk S, et al. Investigating the mechanism of stress corrosion cracking of controllable rolling pipe steel X70 in near-neutral environment[J]. Materials Today:Proceedings, 2022, 50: 470 − 476. doi: 10.1016/j.matpr.2021.11.294 [10] Scott P M, Combrade P. General corrosion and stress corrosion cracking of Alloy 600 in light water reactor primary coolants[J]. Journal of Nuclear Materials, 2019, 524: 340 − 375. doi: 10.1016/j.jnucmat.2019.04.023 [11] Kang S S, Hwang S S, Kim H P, et al. The experience and analysis of vent pipe PWSCC (primary water stress corrosion cracking) in PWR vessel head penetration[J]. Nuclear Engineering and Design, 2014, 269: 291 − 298. doi: 10.1016/j.nucengdes.2013.08.043 [12] 王泽军, 卢惠屏, 荆洪阳. 加热面积对球罐局部热处理应力消除效果的影响[J]. 焊接学报, 2008, 29(3): 125 − 128,159. doi: 10.3321/j.issn:0253-360X.2008.03.032 Wang Zejun, Lu Huiping, Jing Hongyang. Effect of heating area on stress relief of local heat treatment[J]. Transactions of the China Welding Institution, 2008, 29(3): 125 − 128,159. doi: 10.3321/j.issn:0253-360X.2008.03.032 [13] 汪建华, 陆皓, 魏良武, 等. 局部焊后热处理两类评定准则的研究[J]. 机械工程学报, 2001, 37(6): 24 − 28. doi: 10.3901/JME.2001.06.024 Wang Jianhua, Lu Hao, Wei Liangwu, et al. Study on two types of evaluation criteria for local post weld heat treatment[J]. Journal of Mechanical Engineering, 2001, 37(6): 24 − 28. doi: 10.3901/JME.2001.06.024 [14] British Standard Institution. PD 5500: 2015. Specification for unfired fusion welded pressure vessels [S]. London: British Standard Institution, 2015. [15] The Standards Policy and Strategy Committee. EN 13445-4: 2009 Unfired pressure vessels-Part4: Fabrication[S]. London: British Standard Institution, 2009. [16] 陆皓, 汪建华, 村川英一. Cr-Mo钢管子局部焊后热处理加热宽度准则的确定[J]. 焊接学报, 2006, 27(3): 5 − 8,113. Lu Hao, Wang Jianhua, Murakawa Y Y. Determination of Heating Width Criteria for Local Post-weld Heat Treatment of Cr-Mo Steel Pipes[J]. Transactions of the China Welding Institution, 2006, 27(3): 5 − 8,113. [17] 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 30583-2014承压设备焊后热处理规程[S]. 北京: 中国标准出版社, 2014. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. GB/T 30583-2014 Specification for post-welding heat treatment of pressure equipment [S]. Beijing: Standards Press of China, 2014. [18] 蒋文春, 罗云, 万娱, 等. 焊接残余应力计算、测试与调控的研究进展[J]. 机械工程学报, 2021, 57(16): 306 − 328. doi: 10.3901/JME.2021.16.306 Jiang Wenchun, Luo Yun, Wan Yu, et al. Research progress on calculation, measurement and control of welding residual stress[J]. Journal of Mechanical Engineering, 2021, 57(16): 306 − 328. doi: 10.3901/JME.2021.16.306 [19] Houman A, Anna P, Mark R, et al. Effect of holding time on strain relaxation in high-strength low-alloy steel welds: An in-situ neutron diffraction approach[J]. Journal of Manufacturing Processes, 2022, 73: 326 − 339. doi: 10.1016/j.jmapro.2021.11.005 [20] Liu R F, Wang J C. Application of finite element method to effect of weld overlay residual stress on probability of piping failure[J]. International Journal of Pressure Vessels and Piping, 2022, 200: 104812. [21] Song W, Liu X S, Wang P, et al. Strength mismatch effect on residual stress of 10CrNi3MoV steel considering the back-chipping process[J]. International Journal of Pressure Vessels and Piping, 2022, 195: 104570. doi: 10.1016/j.ijpvp.2021.104570 [22] Yu B L, Wang P, Song X G, et al. The residual stress relief of post weld heat treatment in SMA490BW welded joints: Simulation and experiment[J]. International Journal of Pressure Vessels and Piping, 2022, 200: 104852. doi: 10.1016/j.ijpvp.2022.104852 [23] Gan Shiming, Liu Huaying, Zhai Zhiping, et al. A review of welding residual stress test methods[J]. China Welding, 2022, 31(2): 45 − 55. [24] Dai P, Wang Y, Li S, et al. FEM analysis of residual stress induced by repair welding in SUS304 stainless steel pipe butt-welded joint[J]. Journal of Manufacturing Processes, 2020, 58: 975 − 983. doi: 10.1016/j.jmapro.2020.09.006 -
点击查看大图
计量
- 文章访问数: 10
- HTML全文浏览量: 0
- PDF下载量: 7
- 被引次数: 0
