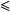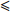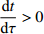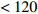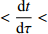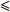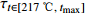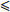Design of reflow oven furnace temperature based on quantum multi-objective optimization algorithm
-
摘要: 电路板焊接中心点的温度走势间接地反映了焊接质量，炉温曲线的优化设计对提高电路板焊接质量有着举足轻重的作用.文中运用傅里叶定律和集总参数法，建立反映电路板焊接中心温度变化的非稳态导热模型，并在满足制程界限和工艺要求的约束条件下，以传送带过炉速度最优和加热因子最小为目标，采用量子多目标粒子群算法(quantum multi-objective particle swarm optimization，QMOPSO)进行优化求解，获得了各温区的最优温度和电路板的最大过炉速度，并得到了最优炉温曲线.结果表明，优化后的电路板过炉速度为95.55 cm/min，接近速度上限，加热因子最小值为1753.04，炉温曲线整体呈现先上升后下降的趋势，峰值温度为240.01 ℃，接近温度制程界限下限，该结果为电路板等电子器件焊接工艺的实际工程应用和提高焊接质量提供参考.Abstract: The temperature trend of the welding center of circuit board indirectly reflects the welding quality. The optimization design of furnace temperature curve plays an important role in improving the welding quality of circuit board. In this paper, Fourier law and lumped parameter method were used to establish the unsteady heat conduction model reflecting the temperature change of the welding center of the circuit board. Under the constraints of meeting the process limits and technological requirements, the quantum multi-objective particle swarm optimization algorithm was used to optimize the solution with the goals of the optimal conveyor belt passing furnace speed and the minimum heating factor. The optimum temperature of each temperature region, the maximum passing speed of circuit board and the optimum temperature curve were obtained. The results show that the optimized circuit board passing through the furnace speed is 95.55 cm/min, which is close to the upper limit of the speed limit, and the minimum heating factor is 1 753.04. The furnace temperature curve shows a trend of rising first and then decreasing. The peak temperature is 240.01 ℃, which is close to the lower limit of the temperature process. The results provide strong guidance for practical engineering application and improvement of welding quality of electronic devices such as circuit boards.
-
0. 序言
回焊炉炉温曲线反映了焊接过程中焊点的温度变化情况[1]，影响炉温曲线调节的因素一般有炉温曲线峰值温度、升温速率、电路板上的温度分布、预热时间等[2-5].若回焊炉各小温区温度调节不良，会导致电路板变色变形、空洞、润湿不良等，影响产品焊接质量和可靠性[6]，因此可以通过对炉温曲线的优化设计来提高焊接质量.
针对炉温曲线优化设计，李楠等人[7]在RSS (Ramp-Soak-Spike)升温-保温-峰值曲线基础上，利用牛顿冷却定律建立传热模型，运用数值计算的方法进行求解，得到通过控制传送带速度和温区温度会提高焊接质量的结论，获得了模拟炉温曲线，但该方法未考虑温区间隙对回焊炉温度场的影响，会导致最终炉温曲线在相邻温区过渡时仿真效果较差.王明泉等人[8]基于傅里叶定律建立一维偏微分热传导模型，运用有限差分法求解炉温曲线优化参数，研究如何通过控制温区温度提高产品质量，为实际生产提供理论支持，但该求解方法的计算精度还有待提高.方灏航等人[9]利用Fourier定律和牛顿冷却定律，建立炉温曲线差分模型，运用模拟退火算法全局寻优，获得高经济效益基础上的最大过炉速度和各温区的最优稳定温度，然而模拟退火算法可能无法得到全局最优解，影响计算结果.Lei等人[10]建立热传导方程模型，使用经典粒子群算法计算热导率并进行误差分析，利用蒙特卡罗仿真(Monte Carlo simulation)[11]得到传送带的最大速度，但该算法易于陷入局部最优解，对仿真结果产生影响.祝胜光等人[12]提出一种小型智能数控回焊炉温度控制器的设计和实现方法，采用PID算法控制温度，缩短调节时间，提高温控精度.综上可知，目前在研究炉温曲线模型参数时大多采用数值解法和传统优化算法，计算繁琐，计算结果的精确性和收敛性还有待提高；在炉温曲线优化设计时，均采用单一目标进行优化，没有综合考虑其它因素影响，整体实用性较差.因此，设计一种有效的方法来解决多目标炉温曲线优化问题十分必要.
量子粒子群优化算法(quantum particle swarm optimization，QPSO)是Sun等人[13]基于量子力学提出的一种新的粒子群优化算法.该算法因实现简单方便、搜索高效准确、迭代收敛快速、结果预测精准、需要控制的参数少，全局搜索能力强，被广泛用于处理各种工程实际优化问题[14-17].文中运用QPSO算法，在满足制程界限的同时，以加热因子[18]最小和传送带速度最优为目标，对回焊炉炉温曲线进行优化设计，为解决目标冲突的回焊炉温区温度设置提供一种解决方案.
1. 炉温曲线模型建立
1.1 基本参数
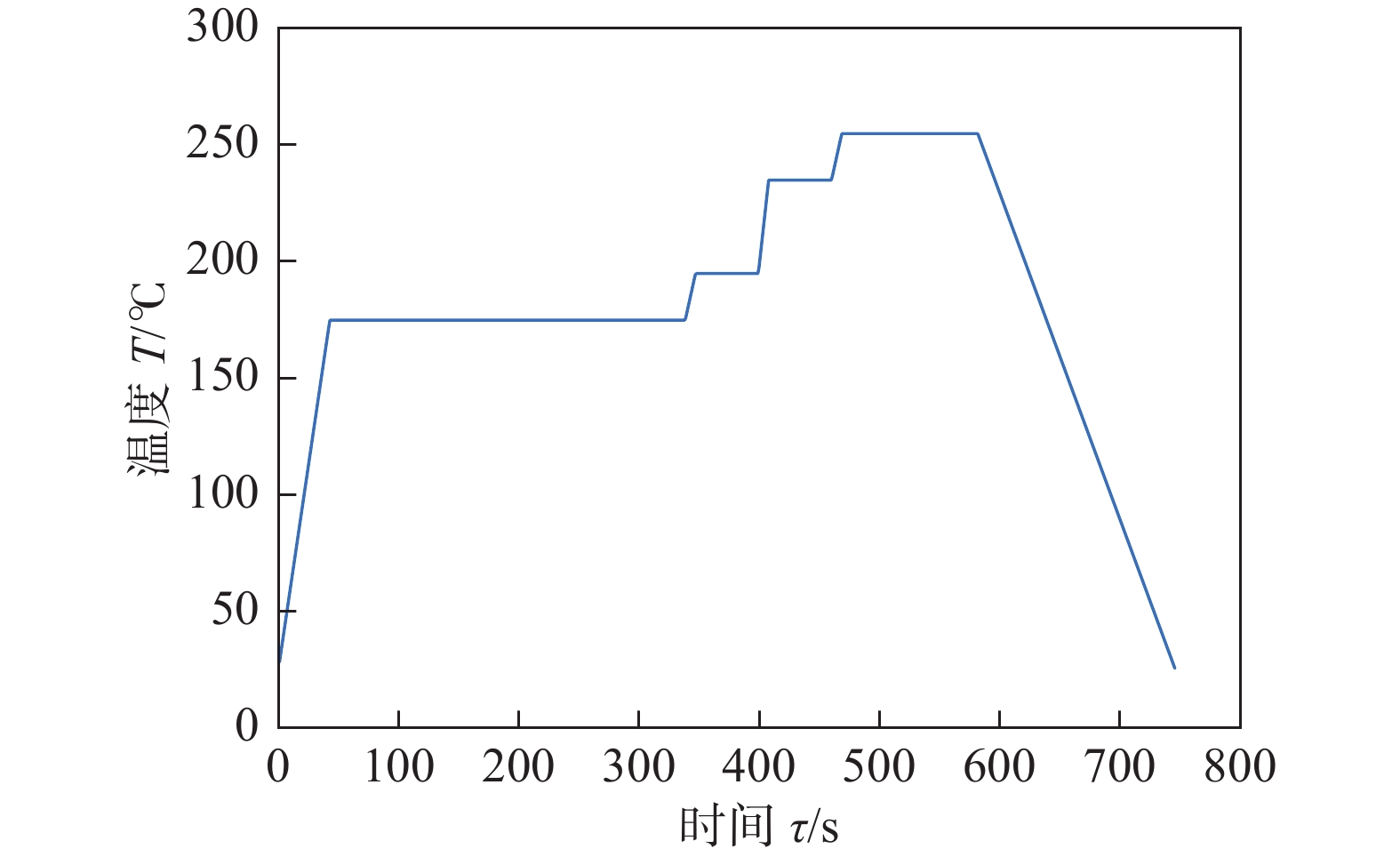
电子元器件的焊接过程会经历炉前区域、炉内区域和炉后区域.根据回焊炉内部各区段温度和功能的不同可分为预热区段、恒温区段、回流区段、冷却区段，并分为11个小温区.环境温度为25 ℃，回焊炉各温区长度和温度见表1.
表 1 回焊炉各温区长度和温度Table 1. Length and temperature of each temperature zone in rewelding furnace区域 长度l/cm 温度T/℃ 炉前 25 25 1 ~ 5 172.5 175 6 30.5 195 7 30.5 235 8 ~ 9 66 255 10 ~ 11 66 25 炉后 25 25 间隙 5 — 1.2 基本假设
由于受到模拟和实际研究难度的限制，将忽略回焊炉内温度场热辐射的传热；假设电路板的材料均匀，具有各向同性，忽略其内部温差，温度分布均匀；假设电路板进入温区瞬间其内部温度保持稳定且不变；由于电路板厚度较小，其沿厚度方向的热传导将忽略.
1.3 热传导模型
通过已知各小温区温度可获得回焊炉内温度随时间的数学表达式.各小温区温度恒定不变，则对应回焊炉内温度场的温度恒定不变；相邻温区若不存在温差，则温区间隙温度也恒定不变；反之，间隙温度呈线性变化.
对于回焊炉空间内的物体而言，可建立三维非稳态导热微分方程，如式(1)所示[19].
$$ {{\rho c}}\frac{{{{\partial}} T}}{{\partial \tau }} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\lambda \frac{{\partial T}}{{\partial z}}} \right) + \dot \varPhi $$ (1) 式中：
$ \tau $ 为时间；$ T $ 为回焊炉内的温度场温度；$ {{\rho }} $ 为密度；$ {{c}} $ 为比热容；$ \lambda $ 为导热系数；$ \dot \varPhi $ 为单位时间单位体积中的内热源生成热；x，y，z分别为该物体在空间x，y和z 3个方向上的坐标值.由于各间隙的边界温度稳定不变，可将式(1)简化为一维稳态无内热源常物性导热微分方程，如式(2)所示.
$$ \frac{{{\partial ^2}T}}{{\partial {x^2}}} = 0 $$ (2) 对式(2)进行微分求解，可得温区间隙处的温度分布，如式(3)所示.
$$ {T_{{i}}} = {{{\varepsilon }}_{{i}}}{x_{{i}}} + {{{\beta }}_{{i}}} $$ (3) 式中：i表示温区区段，
$i = 0,1,2,3\cdots$ ；${{{\varepsilon }}_{{i}}}$ ，${{{\beta }}_{{i}}}$ 为第$ i $ 温区的常数参数；${x_{{i}}}$ 为炉前到第i温区与(i + 1)温区之间间隙的距离；${T_{{i}}}$ 表示第i温区处对应的温度场温度.回焊炉各小温区间隙温度的线性分布如式(4)所示.
$$ \left\{ {\begin{array}{*{20}{l}} {{T_{{i}}} = {{{\varepsilon }}_{{i}}}{x_{{{{i}}_{{{\rm{e}}}}}}} + {{{\beta }}_{{i}}}} \\ {{T_{{{i}} + 1}} = {{{\varepsilon }}_{{i}}}{x_{{{\left( {{{i}} + 1} \right)}_{{{\rm{s}}}}}}} + {{{\beta }}_{{i}}}} \end{array}} \right. $$ (4) 式中：v表示电路板的过炉速度；
${x_{{{{i}}_{{{\rm{e}}}}}}} = v{t_{{{{i}}_{{{\rm{e}}}}}}}$ 表示为从炉前到离开第i温区区段的距离；${x_{{{(i + 1)}_{{{\rm{s}}}}}}} = $ $ v{t_{{{({{i}} + 1)}_{{{\rm{s}}}}}}}$ 表示从炉前到进入第$ i + 1 $ 温区区段开始位置的距离.1.4 电路板焊接中心温度模型
电路板进入回焊炉瞬间，其内部温度保持不变，随后焊接中心温度随时间开始发生变化，最终趋近于回焊炉的温度场温度，故可将其简化为非稳态、有内热源的导热微分方程，如式(5)所示.
$$ \left\{ {\begin{array}{*{20}{l}} {\dfrac{{\partial t}}{{\partial \tau }} = a{\nabla ^2}t + \dfrac{{\dot \varPhi }}{{{{\rho c}}}}} \\ {a = \dfrac{\lambda }{{{{\rho c}}}}} \end{array}} \right. $$ (5) 式中：t为焊接中心温度；
$ a $ 为热扩散系数.由于焊接中心处吸收的热量与焊接表面上的对流换热量相等，得到热平衡公式，如式(6)所示.
$$ {Q_{\rm{a}}} = Q $$ (6) 式中：
${Q_{\rm{a}}}$ 为焊接中心处吸收的热量.采用牛顿冷却定律建立界面换热模型，如式(7)[20]所示.
$$ {{c}} \cdot \frac{{{\rm{d}}t(h,\tau )}}{{{\rm{d}}\tau }} \cdot {{\rho V}} = - h(T){{A}}[t(h,\tau ) - {T_{{i}}}] $$ (7) 式中：
$ h(T) $ 为回焊炉温度场内空气流体与电路板之间的对流换热系数；A为换热面积；V为体积.将式(7)化简，即$$ {\rm{d}}Q = {{\rho cV}}{\rm{d}}\theta = - h(T){t{A}}\theta {\rm{d}}\tau $$ (8) 式中：
$\theta = t(h,\tau ) - {T_{{i}}}$ 为过余温度.边界条件为初始温度，如式(9)所示.$$ \theta (i) = {t_{{i}}} - {T_{{i}}} = {\theta _{{i}}} $$ (9) 式中：
${t_{{i}}}$ 为进入第i温区时焊接中心的初始温度；${\theta _{{i}}}$ 为进入第i温区时焊接中心的初始过余温度.综上所述，可得到焊接中心处温度变化表达式，如式(10)所示[21].
$$ \begin{gathered} t(h,\tau ) = ({t_{{i}}} - {T_\infty })\exp \left( - \frac{{h(T){{A}}}}{{{{\rho cV}}}}\tau \right) + {T_\infty } = \\ {t_{{i}}}\exp \left( - \frac{\tau }{{R{C_{{i}}}}}\right) + {T_\infty }\left[ {1 - \exp \left( - \frac{\tau }{{R{C_{{i}}}}}\right)} \right] \\ \end{gathered} $$ (10) 式中：
$T_\infty $ 为回焊炉温度场内经一段时间传热后恒定不变时温度场的温度；取$R{C_i} = \dfrac{{{\rho cV}}}{{{h_i}(T)A}}$ ，i = 0,1,2···10，$R{C_{{i}}}$ 的值仅与回焊炉内流体温度有关；$h_i(T) $ 表示第i温区回焊炉温度场内空气流体与电路板之间的对流换热系数.2. 多目标炉温曲线优化模型
加热因子是指使回焊炉炉温曲线温度从锡膏熔点温度到峰值温度所覆盖的面积，即回焊炉炉温曲线液相线以上的温度对时间的积分[22-24]，文中采用无铅常规锡膏，熔点为217 ℃.在建立焊接中心温度变化模型的基础上，以加热因子最小和传送带速度最大为目标，利用量子粒子群算法进行多目标优化，进而获得最优回焊炉炉温曲线.
2.1 目标函数1：加热因子最小
为使加热因子最小，建立目标函数如式(11)所示.
$$\begin{split} {S_{{\rm{cover}}}} = & \min \left( {\left| {\left. {\int_{{\tau _{\rm{a}}}}^{{\tau _{\max }}} {(t(h,\tau ) - {{{t}}_{\rm{a}}}){\rm{d}}\tau } } \right|} \right. + } \right.\\ & \left. {\left| {\left. {\int_{{\tau _{\max }}}^{{\tau _{\rm{b}}}} {(t(h,\tau ) - {{{t}}_{\rm{a}}}){\rm{d}}\tau } } \right|} \right.} \right) \end{split} $$ (11) 式中：ta为无铅常规锡膏熔点，ta = 217 ℃；
${S_{{{\rm{cov}}} {\rm{er}}}}$ 表示加热因子；$ {\tau _a} $ 表示焊接中心温度第一次达到ta的时间；$ {\tau _{\max }} $ 表示焊接中心温度达到峰值温度的时间；$ {\tau _{\rm{b}}} $ 表示焊接中心温度第二次达到ta的时间.2.2 目标函数2：最优传送带速度
传送带速度最优，即在满足炉温曲线制程界限和工艺要求的前提下过炉速度最大，如式(12)所示.
$$ {V_{{\rm{best}}}} = \max v $$ (12) 式中：
${V_{{\rm{best}}}}$ 为电路板的最大过炉速度.2.3 约束条件
约束条件包括传送带的过炉速度、炉温曲线的峰值温度和焊接中心温度的变化速率、预热时间、焊接区域温度超过无铅常规锡膏熔点所用时间.
实际生产时传送带速度需满足速度限值，如式(13)所示.
$$ 65{\text{ cm}}/\min \leqslant v \leqslant 100{\text{ cm}}/\min $$ (13) 电路板在焊接生产过程中，炉温曲线需满足的制程界限如表2所示.
表 2 传送带速度需满足的制程界限Table 2. Process limits for conveyor speed炉温曲线峰值温度 T/℃ 焊接中心升温过程中位于
[150 ℃, 190 ℃]温度区间的时间 τt/s焊接中心温度变化速率(dt/di)/(℃·s−1) 焊接中心温度位于[217 ℃，tmax]温度
区间的时间 τt/s240 $\leqslant $ tmax$\leqslant $250 $\dfrac{\text{d}t}{\text{d}\tau } > 0$
且60 < τt∈[150 ℃，190 ℃] $ < 120 $−3 $ < \dfrac{\text{d}t}{\text{d}\tau } < $ 3 40 $\leqslant $ ${\tau _{t \in [217\;{\text{℃} },\;{ { {t_{\max } }]} }} }$ $\leqslant $ 90 3. 量子粒子群算法
在量子粒子群优化算法中，将粒子的搜索空间从经典空间转化为量子空间，并使用薛定谔方程的波函数对量子空间中的粒子状态进行表述.由于局部吸引子，粒子将最终会聚集到某个区域，其如式(14)[25]所示.
$$ {p_{{{oj}}}}(d) = {\varphi _{{{oj}}}}(d){G_{{{oj}}}}(d) + \left[ {1 - {\varphi _{{{oj}}}}(d)} \right]{Z_{{j}}} $$ (14) 式中：o为粒子数；j为解空间维数；d为迭代次数；poj(d)为局部吸引子；Goj(d)为粒子的个体最佳位置；Zj为种群的全局最佳位置；
$ {\varphi _{{{oj}}}}(d) $ 是区间(0,1)上具有均匀概率密度函数的随机数.在解空间中，粒子根据量子阱和波函数给出的密度函数向阱中心收敛，然后使用式(15)和式(16)更新所有粒子.
$$ {X_{{{oj}}}}(t + 1) = {p_{{{oj}}}(d)} \pm u \left| {Pbes{t_{{j}}}\left( d \right) - {X_{{{oj}}}}(d)} \right| \ln \left(\frac{1}{r}\right) $$ (15) $$ Pbes{t_{{j}}}\left( d \right) = \frac{1}{M}\sum\limits_{o = 1}^M {{P_{{{oj}}}}\left( d \right)} $$ (16) 式中：Xoj(d + 1)为粒子o在第(d + 1)次迭代中的位置；u为收缩扩张因子，以控制量子粒子群的收敛速度，介于[0，1]之间的服从均匀分布的随机数；
$Pbes{d_{{j}}}\left( d \right)$ 为粒子群的平均最优位置；r为在区间(0,1)上分布的随机数；M为种群规模.为了避免人为因素对最优结果选择的影响，利用模糊隶属函数[26]从帕累托(pareto)最优解集中选择合适的加热方案.模糊隶属函数计算的综合满意度值越大，说明求解的结果越好.模糊隶属函数如式(17)所示.
$$ \left\{ {\begin{array}{*{20}{c}} {\varphi _l^k = \dfrac{{f_{{k}}^{\max } - {f_{{k}}}({x_{\rm{m}}})}}{{f_{{k}}^{\max } - f_{{k}}^{\min }}}} \\ {{\varphi _{{k}}} = \dfrac{{\displaystyle\sum\nolimits_{{{k}} = 1}^{{N_{{\rm{obj}}}}} {\varphi _{{l}}^k} }}{{\displaystyle\sum\nolimits_{{{l}} = 1}^{{N_{\text{f}}}} {\displaystyle\sum\nolimits_{{{k}} = 1}^{{N_{{\rm{obj}}}}} {\varphi _{\rm{l}}^k} } }}} \end{array}} \right. $$ (17) 式中：
${\varphi _{{k}}}$ 为对所有目标函数的总体满意程度，${\varphi _{{k}}}$ 值越高说明解越好；$ \varphi _l^k $ 表示第l个目标的帕累托最优解xm的满意度；$f_{{k}}^{\max }$ 和$f_{{k}}^{\min }$ 分别为第k个目标函数的最大值和最小值；Nf为帕累托解的个数；k为目标数；Nobj为目标函数的数量[27].基于量子多目标粒子群算法的炉温曲线优化设计的算法流程如下.
(1)设定外部档案最大储存量Lmax、种群规模M等，根据制程界限确定可行解，在可行解中随机初始化粒子群的位置.
(2)根据公式(11)和公式(12)计算适应度值，将非劣解存入外部档案中，确定粒子个体最优位置及全局最优位置.
(3)根据公式(15)和公式(16)计算粒子群的平均最优位置，并更新粒子状态.
(4)判断更新后的粒子是否满足制程界限，若满足，则根据式(11)和式(12)计算该粒子的适应度值；若不满足，则舍弃该粒子.
(5)利用pareto原则更新非劣解集，并将其存入外部档案.
(6)利用拥挤度排序法完成外部档案更新.
(7)判断是否满足终止条件，若不满足则返回step3重复计算直到达到最大迭代次数或满足终止条件.
(8)利用模糊规则从pareto解集中选择最终方案.
4. 模型求解和结果分析
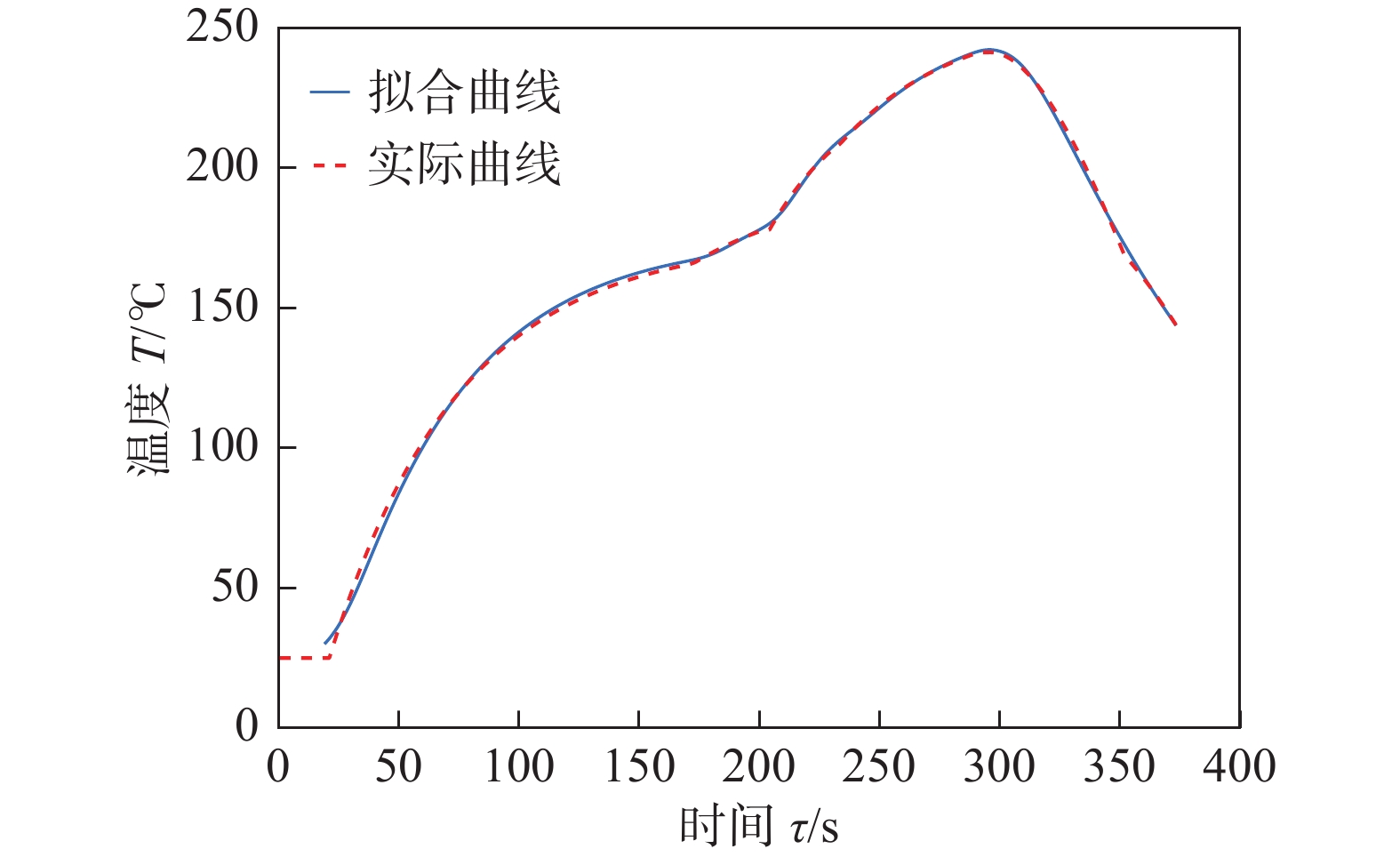
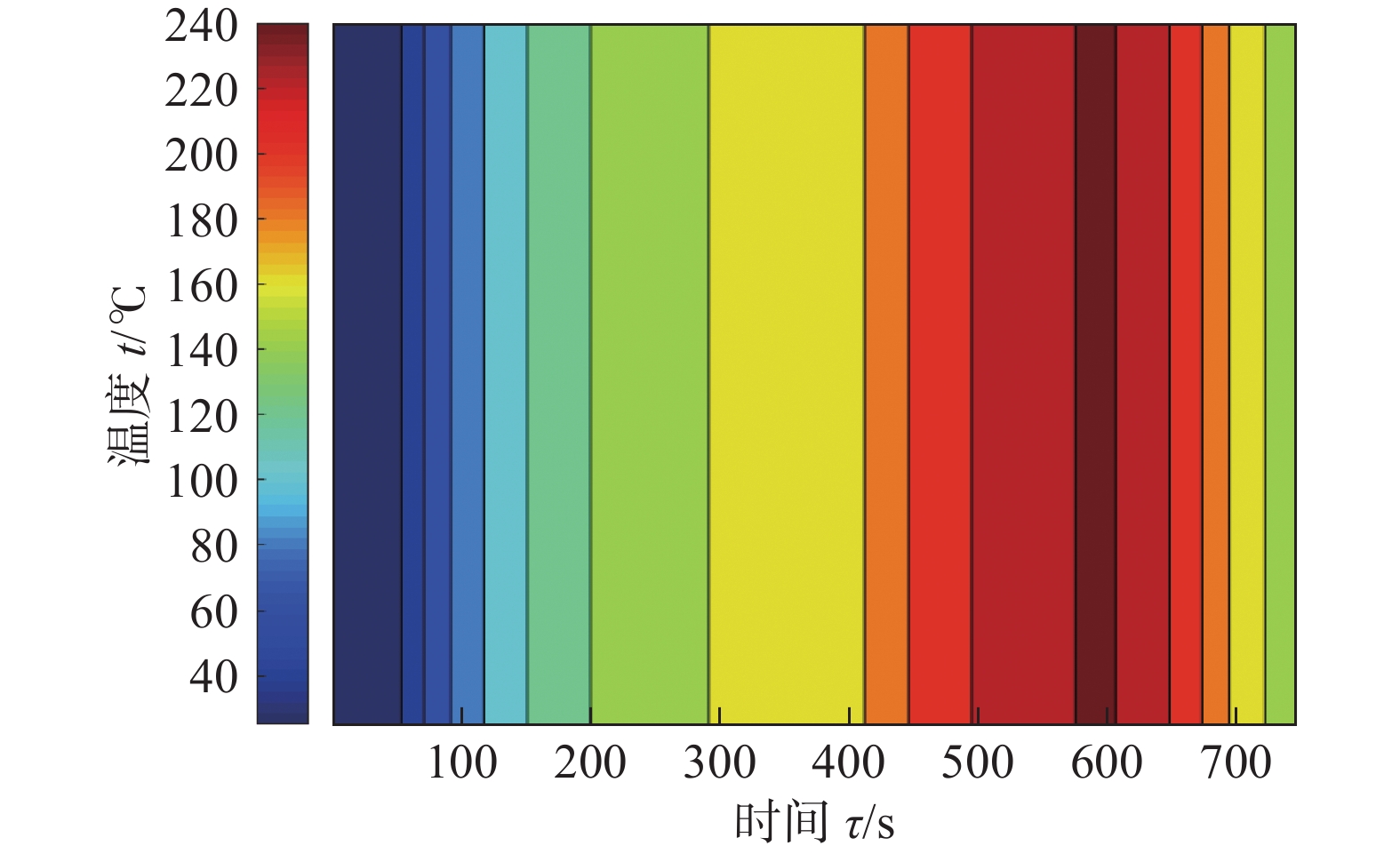
根据1.3节建立的热传导模型通过仿真模拟获得回焊炉温度场的温度分布曲线如图1所示.以回焊炉基本参数为基础，运用量子粒子群算法和最小二乘法拟合求解焊接中心温度变化模型中的待定参数获得模拟炉温曲线，并与测试数据进行对比，如图2所示.电路板焊接中心温度变化分布仿真结果如图3所示.从图2~图3可以很直观的看出，模拟炉温曲线与实测数据曲线的走势大致相同，且收敛较好，验证了所建模型的合理性.
![]()
图 1 回焊炉温度场温度分布曲线Figure 1. Temperature distribution curve of reweld furnace temperature field![]()
图 2 模拟炉温曲线与实测温度曲线对比Figure 2. Comparison between simulated furnace temperature curve and measured temperature curve![]()
图 3 电路板焊接中心温度分布图Figure 3. Temperature distribution diagram of circuit board welding center在上述建立的电路板焊接中心温度模型的基础上，为了验证文中提出的多目标炉温曲线优化模型的有效性，另外设置3组比较情况如下.
(1)以无铅常规锡膏的加热因子最小为优化目标，进行炉温曲线优化设计.
(2)以最优过炉速度为优化目标，进行炉温曲线优化设计.
(3)同时以无铅常规锡膏的加热因子最小和最优过炉速度为优化目标，进行炉温曲线优化设计.
3种不同优化设计情况对比结果如表3所示.由表3可以看出，文中提出的焊接中心温度变化模型可以同时考虑最优过炉速度和最小加热因子.倘若仅考虑最优过炉速度，就会导致加热因子增大，焊接区域中心温度超过无铅常规锡膏熔点的时间过长，降低焊接质量；若仅考虑最小加热因子，则会降低电路板的过炉速度，影响焊接效率.故仅考虑单一目标优化的代价就是影响其它优化目标，进而影响最终优化结果.因此，设计一种可以同时兼顾最优速度和最小加热因子两个目标的焊接中心温度变化模型，获得的最优速度为95.55 cm/min，最小加热因子为1753.04.
表 3 3种不同优化情况结果Table 3. Results of three different optimization conditions目标参数 过炉速度v/(cm·min−1) 加热因子
Scover最小加热因子min (Scover) 94.05 1 027.80 最大过炉速度max (v ) 95.626 2 2 931.56 最小加热因子min (Scover)和
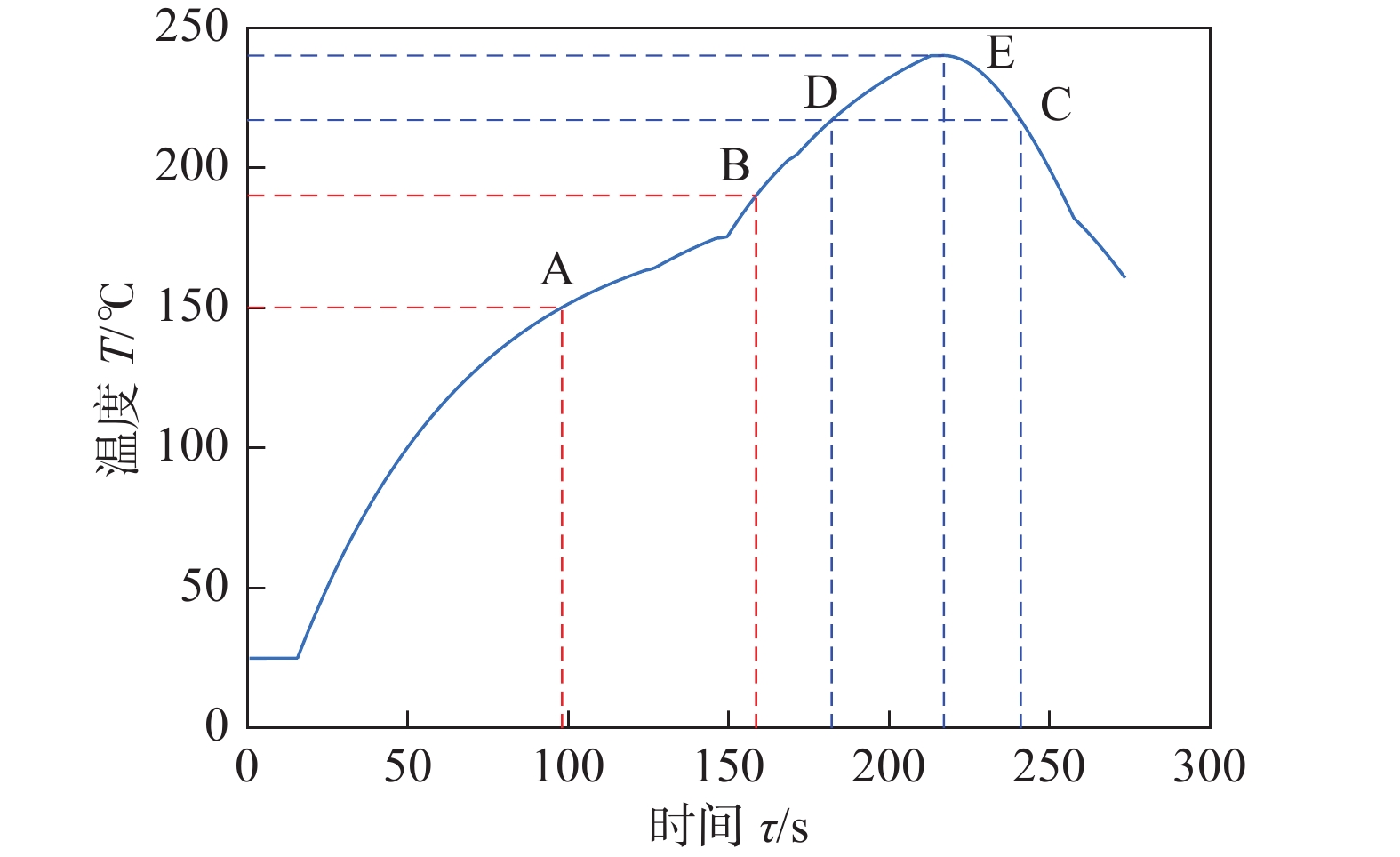
最大过炉速度max (v )95.55 1 753.04 以传送带过炉速度最优和加热因子最小为目标，采用量子多目标粒子群算法进行优化求解，获得各温区的最优炉温曲线如图4所示；图4中A，B，C，D，E点坐标如表4所示；各小温区最优温度值如表5所示.
表 4 优化后炉温曲线内特殊点坐标值Table 4. Coordinate values of special points in the furnace temperature curve after optimization点 坐标 点 坐标 A (98.50，150.11) D (183.00，216.97) B (159.00，190.02) E (219.00，240.01) C (242.50，217.36) 表 5 优化后获得的最优温区温度值Table 5. Optimal temperature value of temperature zone obtained after optimization温区 优化后温度T0/℃ 温区 优化后温度T0/℃ 1~5 184.34 8~9 264.81 6 199.35 10~11 25 7 239.07 相同焊接质量条件下，传送带速度越快越好，优化后的速度为95.55 cm/min，接近速度界限上限.在焊接过程中，为保证焊接质量，焊接区域中心温度超过217 ℃的时间不宜过长，峰值温度也不宜过高，故炉温曲线的温度峰值越低，越接近制程界限，覆盖面积越小，加热因子越小，炉温曲线越理想，优化后的峰值温度为240.01 ℃，接近温度峰值界限下限.
由图4和表5可知，焊接中心升温过程中位于[150 ℃，190 ℃]温度区间的时间为60.5 s，焊接中心温度位于[217 ℃，tmax]温度区间的时间为59.5 s，焊接中心温度变化速率如式(18)所示.
$$ -2.177\;3\;{ {\text{℃}}/{\rm{s}}{}}< \frac{\text{d}t}{\text{d}\tau } < 2.946\;6\;{{ {\text{℃}}/{\rm{s}}}}$$ (18) 5. 结论
(1)以回焊炉炉温曲线为研究对象，在满足制程界限和实际工艺要求的前提下，以传送带速度最优和以无铅常规锡膏的加热因子最小为目标，运用量子多目标粒子群算法对炉温曲线进行优化设计，获得了最大过炉速度和各温区的最优温度.
(2)运用量子粒子群算法和最小二乘法拟合求得焊接中心温度变化模型中的待定参数，获得的模拟炉温曲线与实测数据曲线走势大致相同且收敛较好.
(3)同时兼顾最优速度和最小加热因子两个目标优化后的电路板过炉速度为95.55 cm/min，接近速度界限上限，加热因子最小为1753.04；优化后的炉温曲线整体呈现先上升后下降的趋势，存在一个峰值温度，该峰值温度为240.01 ℃，接近温度峰值界限下限.
-
![]()
图 1 回焊炉温度场温度分布曲线
Figure 1. Temperature distribution curve of reweld furnace temperature field
![]()
图 2 模拟炉温曲线与实测温度曲线对比
Figure 2. Comparison between simulated furnace temperature curve and measured temperature curve
![]()
图 3 电路板焊接中心温度分布图
Figure 3. Temperature distribution diagram of circuit board welding center
表 1 回焊炉各温区长度和温度
Table 1 Length and temperature of each temperature zone in rewelding furnace
区域 长度l/cm 温度T/℃ 炉前 25 25 1 ~ 5 172.5 175 6 30.5 195 7 30.5 235 8 ~ 9 66 255 10 ~ 11 66 25 炉后 25 25 间隙 5 — 
下载: 导出CSV
表 2 传送带速度需满足的制程界限
Table 2 Process limits for conveyor speed
炉温曲线峰值温度 T/℃ 焊接中心升温过程中位于
[150 ℃, 190 ℃]温度区间的时间 τt/s焊接中心温度变化速率(dt/di)/(℃·s−1) 焊接中心温度位于[217 ℃，tmax]温度
区间的时间 τt/s240 $\leqslant $ tmax$\leqslant $ 250$\dfrac{\text{d}t}{\text{d}\tau } > 0$
且60 < τt∈[150 ℃，190 ℃]$ < 120 $ −3 $ < \dfrac{\text{d}t}{\text{d}\tau } < $ 340 $\leqslant $ ${\tau _{t \in [217\;{\text{℃} },\;{ { {t_{\max } }]} }} }$ $\leqslant $ 90
下载: 导出CSV
表 3 3种不同优化情况结果
Table 3 Results of three different optimization conditions
目标参数 过炉速度v/(cm·min−1) 加热因子
Scover最小加热因子min (Scover) 94.05 1 027.80 最大过炉速度max (v ) 95.626 2 2 931.56 最小加热因子min (Scover)和
最大过炉速度max (v )95.55 1 753.04
下载: 导出CSV
表 4 优化后炉温曲线内特殊点坐标值
Table 4 Coordinate values of special points in the furnace temperature curve after optimization
点 坐标 点 坐标 A (98.50，150.11) D (183.00，216.97) B (159.00，190.02) E (219.00，240.01) C (242.50，217.36)
下载: 导出CSV
表 5 优化后获得的最优温区温度值
Table 5 Optimal temperature value of temperature zone obtained after optimization
温区 优化后温度T0/℃ 温区 优化后温度T0/℃ 1~5 184.34 8~9 264.81 6 199.35 10~11 25 7 239.07
下载: 导出CSV
-
[1] Luo X D, Wang Z S, Deng W H. Optimization model design for temperature curve of reflow furnace[J]. Journal of Physics: Conference Series, 2021, 1802(2): 022020.
[2] Harrison M R, Vincent J H, Steen H A H. Lead-free reflow soldering for electronics assembly[J]. Soldering & Surface Mount Technology, 2001, 13(3): 21 − 38.
[3] 陈恒宇,丁唯一,殷寰宇,等.基于量子遗传算法的回焊炉参数设定[J].重庆理工大学学报(自然科学),2021,35(9):248-255. Chen Hengyu, Ding weiyi, Yin Huanyu, et al. Back-welding furnace parameter setting based on the quantum genetic algorithm [J]. Journal of Chongqing University of Technology (Natural Science), 2021,35 (9): 248-255.
[4] 郑风景. 基于六西格玛方法的SMT回流焊产品质量控制研究[D]. 天津: 天津科技大学, 2014. Zheng Fengjing. Research on quality control of SMT reflow soldering process based on the six sigma approach[D]. Tianjin: Tianjin University of Science & Technology, 2014.
[5] 徐宗煌,徐剑莆,李世龙,等. 回焊炉电路板焊接炉温曲线优化模型[J]. 沈阳大学学报(自然科学版), 2021,33(3):279-286. Xu Zonghuang, Xu Jianpu, Li Shilong, et al. Optimization model of welding furnace temperature curve of back-welding furnace circuit board [J]. Journal of Shenyang University (Natural Science Edition), 2021,33 (3): 279-286.
[6] 焦进莉. 六西格玛方法在提升SMT回流焊过程质量中的应用研究[D]. 上海: 上海交通大学, 2011. Jiao Jinli. The application study of six sigma approach on quality improvement of SMT reflow process. [D]. Shanghai: Shanghai Jiaotong University, 2011.
[7] 李楠, 王晓杰, 杜咏昊. 最优炉温曲线与确定其工艺参数问题[J]. 电子测试, 2021(1): 48 − 50. doi: 10.3969/j.issn.1000-8519.2021.01.017 Li Nan, Wang Xiaojie, Du Yonghao. Optimal furnace temperature curve and determination of process parameters[J]. Electronic Test, 2021(1): 48 − 50. doi: 10.3969/j.issn.1000-8519.2021.01.017
[8] 王明泉, 周心如, 李博文. 基于热力学原理的炉温曲线调控模型[J]. 科学技术创新, 2021(1): 1 − 3. doi: 10.3969/j.issn.1673-1328.2021.01.002 Wang Mingquan, Zhou Xinru, Li Bowen. Control model of furnace temperature curve based on thermodynamic principle[J]. Scientific and Technological Innovation, 2021(1): 1 − 3. doi: 10.3969/j.issn.1673-1328.2021.01.002
[9] 方灏航. 基于传热学的炉温曲线研究[J]. 现代信息科技, 2020, 4(20): 18 − 22. Fang Haohang. Furnace temperature curve research based on heat transfer[J]. Modern Information Technology, 2020, 4(20): 18 − 22.
[10] Lei Q Y, Zhang Z Y, Zhuo S Y, et al. Research on furnace temperature curve based on heat convection and heat radiation[J]. E3S Web of Conferences, 2021, 233(9): 04004.
[11] Wealer B, Bauer S, Hirschhausen C V, et al. Investing into third generation nuclear power plants—Review of recent trends and analysis of future investments using Monte Carlo Simulation[J]. Renewable and Sustainable Energy Reviews, 2021, 143: 110836.
[12] 祝胜光, 杨安全. 小型回流焊炉温度PID控制算法研究[J]. 机械工程与自动化, 2012(1): 138 − 140. doi: 10.3969/j.issn.1672-6413.2012.01.054 Zhu Shengguang, Yang Anquan. Study on the temperature PID control algorithm of small reflux welding furnace[J]. Mechanical Engineering & Automation, 2012(1): 138 − 140. doi: 10.3969/j.issn.1672-6413.2012.01.054
[13] Sun J, Wu X J, Palade V, et al. Convergence analysis and improvements of quantum-behaved particle swarm optimization[J]. Information Sciences, 2012, 193: 81 − 103.
[14] Wang F, Zhang H, Zhou A M. A particle swarm optimization algorithm for mixed-variable optimization problems[J]. Swarm and Evolutionary Computation, 2021, 60: 100808. doi: 10.1016/j.swevo.2020.100808
[15] 冯茜, 李擎, 全威,等. 多目标粒子群优化算法研究综述[J]. 工程科学学报, 2021, 43(6): 745-753. Feng Qian, Li Qing, Quan Wei, et al. Overview of multiobjective particle swarm optimization algorithm[J]. Chinese Journal of Engineering, 2021, 43(6): 745-753.
[16] Zhang D G, Wang J X, Fan H R, et al. New method of traffic flow forecasting based on quantum particle swarm optimization strategy for intelligent transportation system[J]. International Journal of Communication Systems, 2020, 34(1): e4647.
[17] 邱幸运. 基于量子粒子群算法的工程项目多目标优化研究[D]. 邯郸: 河北工程大学, 2019. Qiu Xingyun. Multi-objective optimization of engineering projects based on quantum-behaved particle swarm optimization [D]. Handan: Hebei University of Engineering, 2019.
[18] Gao J G, Wu Y P, Ding H. Optimization of a reflow soldering process based on the heating factor[J]. Soldering & Surface Mount Technology, 2007, 19(1): 28 − 33.
[19] Campo A, Arici M. Lucid characterization of unsteady heat conduction in large, square crossbars and cubes subject to uniform surface heat flux by way of “quasi-steady” Helmholtz equations[J]. Thermal Science and Engineering Progress, 2020, 20: 100724. doi: 10.1016/j.tsep.2020.100724
[20] Yang Z. Investigation on the thermal problems of wet clutches for the tracked DCT vehicle during the launching process[J]. IOP Conference Series Materials Science and Engineering, 2020, 892: 012046. doi: 10.1088/1757-899X/892/1/012046
[21] 郭安柱, 马永志. 空调房数学建模与仿真[J]. 科学技术创新, 2020(12): 120 − 122. Guo Anzhu, Ma Yongzhi. Mathematical modeling and simulation of air-conditioned room[J]. Scientific and Technological Innovation, 2020(12): 120 − 122.
[22] Gao J G, Wu Y P, Ding H, et al. Thermal profiling: a reflow process based on the heating factor[J]. Soldering & Surface Mount Technology, 2008, 20(4): 20 − 27.
[23] 李岩, 赵立博, 张伟, 等. 对回流焊炉温度设定的分析与优化[J]. 船电技术, 2010, 30(7): 44 − 46. doi: 10.3969/j.issn.1003-4862.2010.07.012 Li Yan, Zhao Libo, Zhang Wei, et al. Analysis and optimization on the temperature settings of reflow soldering furnace[J]. Marine Electric & Electronic Engineering, 2010, 30(7): 44 − 46. doi: 10.3969/j.issn.1003-4862.2010.07.012
[24] 高金刚. 表面贴装工艺生产线上回流焊曲线的优化与控制[D]. 上海: 上海交通大学, 2007. Gao Jingang. Optimization and control of reflow soldering profile in SMT line[D]. Shanghai: Shanghai Jiaotong University, 2007.
[25] Zhao Y X, Song X T, Wang F, et al. Multiobjective optimal dispatch of microgrid based on analytic hierarchy process and quantum particle swarm optimization[J]. Global Energy Interconnection, 2020, 3(6): 562 − 570. doi: 10.1016/j.gloei.2021.01.008
[26] Wang R J. Multi-objective configuration optimization method for a diesel-based hybrid energy system[J]. Energy Reports, 2020, 6: 2146 − 2152. doi: 10.1016/j.egyr.2020.08.004
[27] Hou H, Liu P, Xiao Z F, et al. Capacity configuration optimization of standalone multi-energy hub considering electricity, heat and hydrogen uncertainty[J]. Energy Conversion and Economics, 2021, 2(3): 122 − 132.
-
期刊类型引用(6)
1. 董博文，史光远，钟素娟，董显，程亚芳，龙伟民，张冠星. 钎料短流程成型技术研究现状（英文）. 稀有金属材料与工程. 2025(02): 377-384 . 
百度学术
2. 夏月庆，杜强，郭鹏，秦建，路全彬，丁宗业，李鹏，董红刚，纠永涛，周培林，张秀丽. 钛/钢异质金属压力焊与钎焊研究进展. 精密成形工程. 2025(03): 67-80 . 百度学术
3. 梁伊茗，赵明远，盛兰兵，沈元勋，钟素娟. 钛合金钎焊界面与熔蚀调控研究现状. 焊接. 2025(04): 66-77 . 百度学术
4. 李鹏，王景宽，秦志伟，丁志杰，马雄，姚佳，孙华为，程亚芳，常云峰，董红刚. TiZrNiCoNbSn高熵钎料钎焊Ti_2AlNb合金接头微观组织与性能. 精密成形工程. 2025(04): 217-225 . 百度学术
5. 田晓羽，张志伟，周晨，赵连清，田洋光，付伟，宋晓国. 钎焊温度对BNi-2非晶钎料钎焊1Cr18Ni9Ti不锈钢组织和性能的影响. 焊接学报. 2024(06): 61-67 . 本站查看
6. 李鹏，张振阳，张亮亮，马雄，孙兵兵，李超，董红刚. (TiZrHf)_(40)(NiCu)_(55)Al_5高熵非晶钎料真空钎焊Ti_2AlNb/GH4169合金. 焊接学报. 2024(08): 1-11 . 本站查看
其他类型引用(0)
计量
- 文章访问数: 220
- HTML全文浏览量: 35
- PDF下载量: 29
- 被引次数: 6
