Numerical simulation of welding residual stress and distortion in T2-Y/Q345 dissimilar materials
-
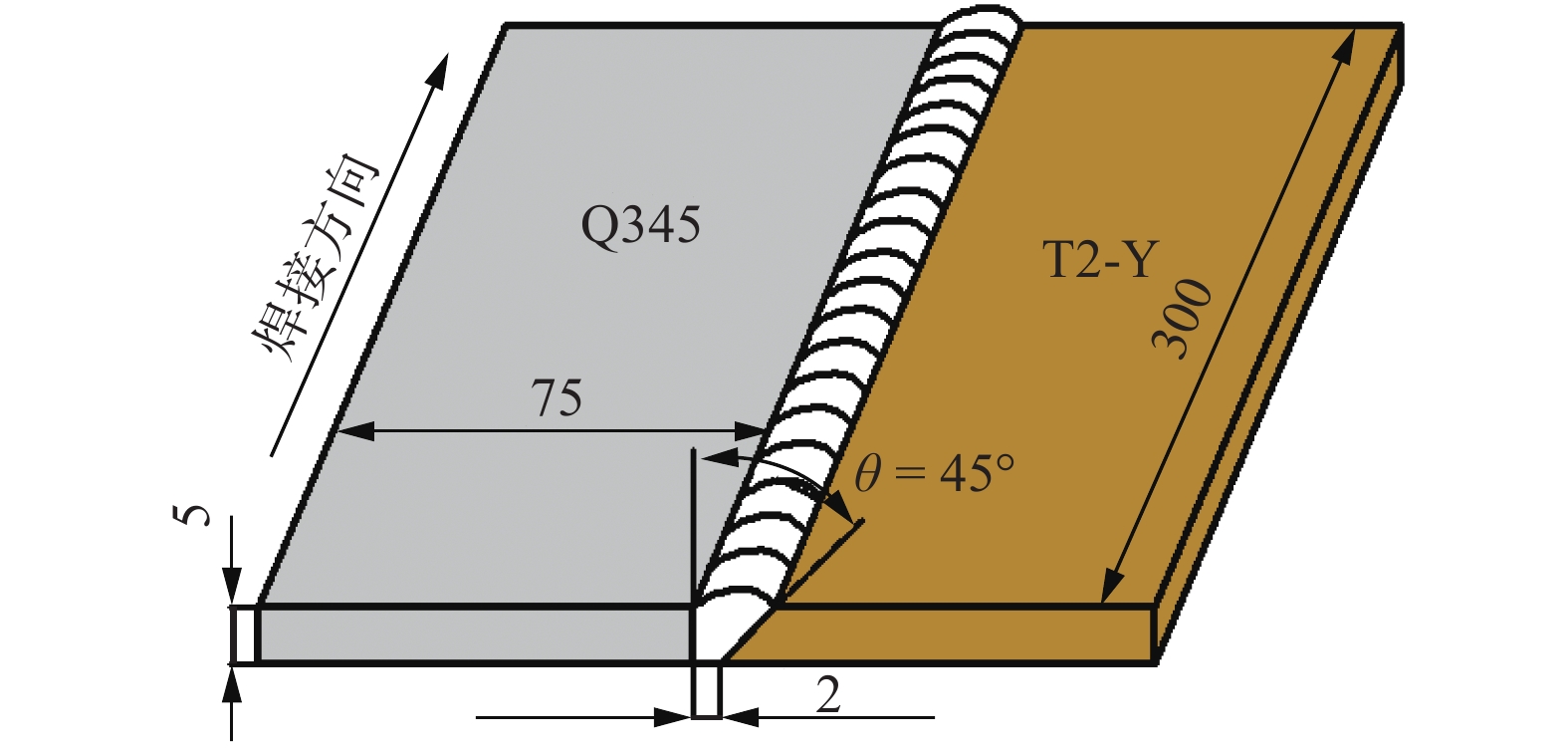
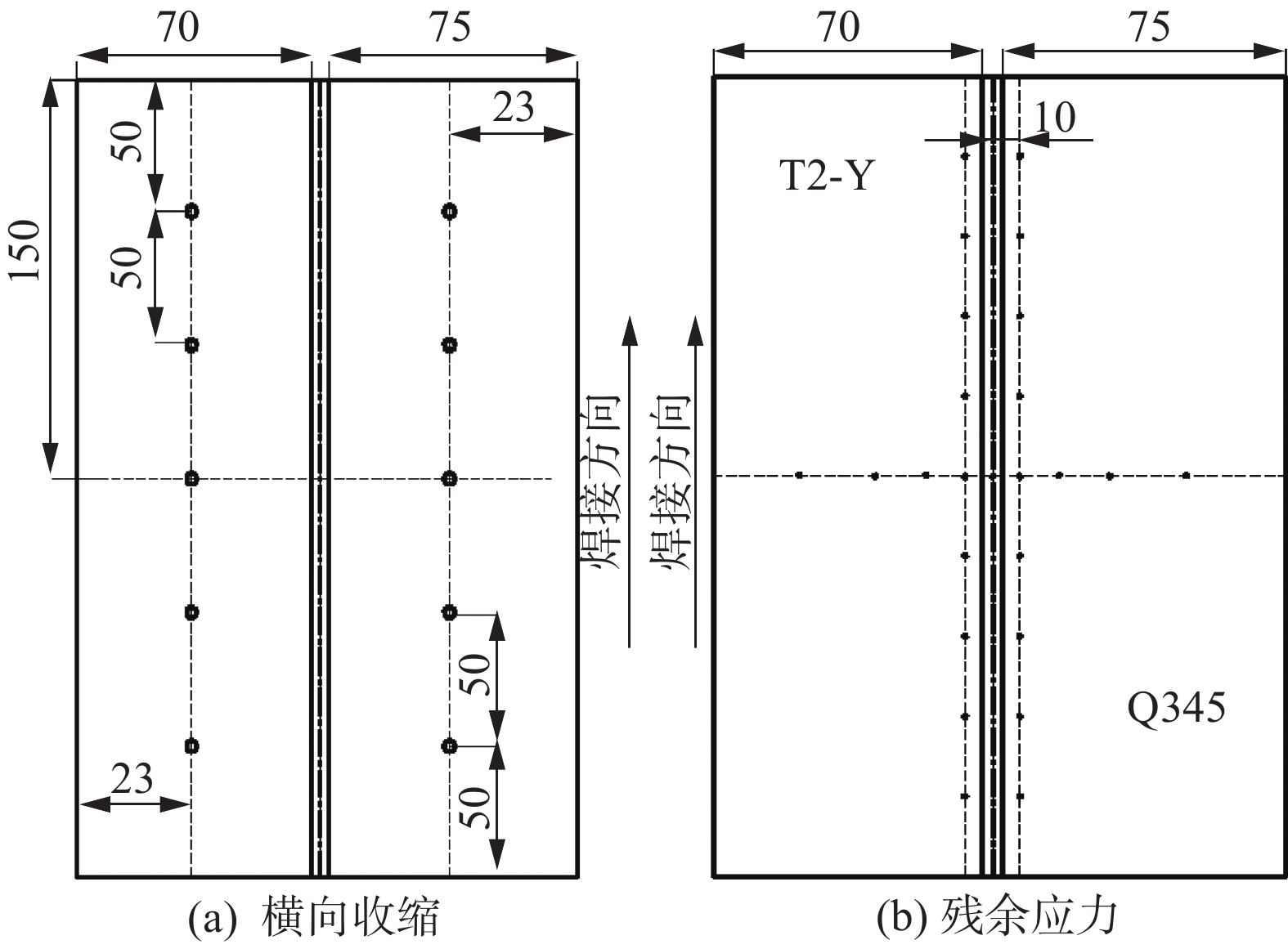
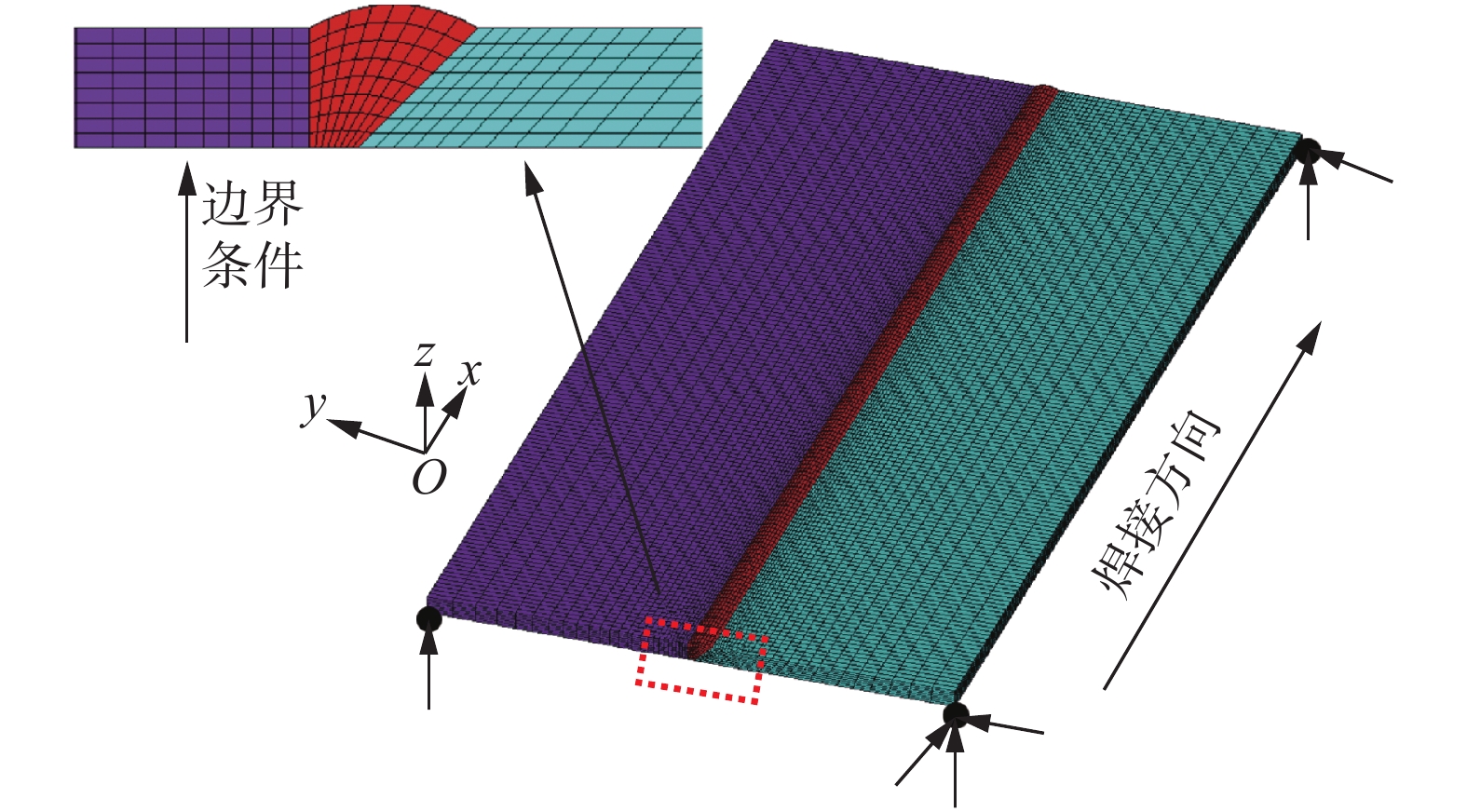
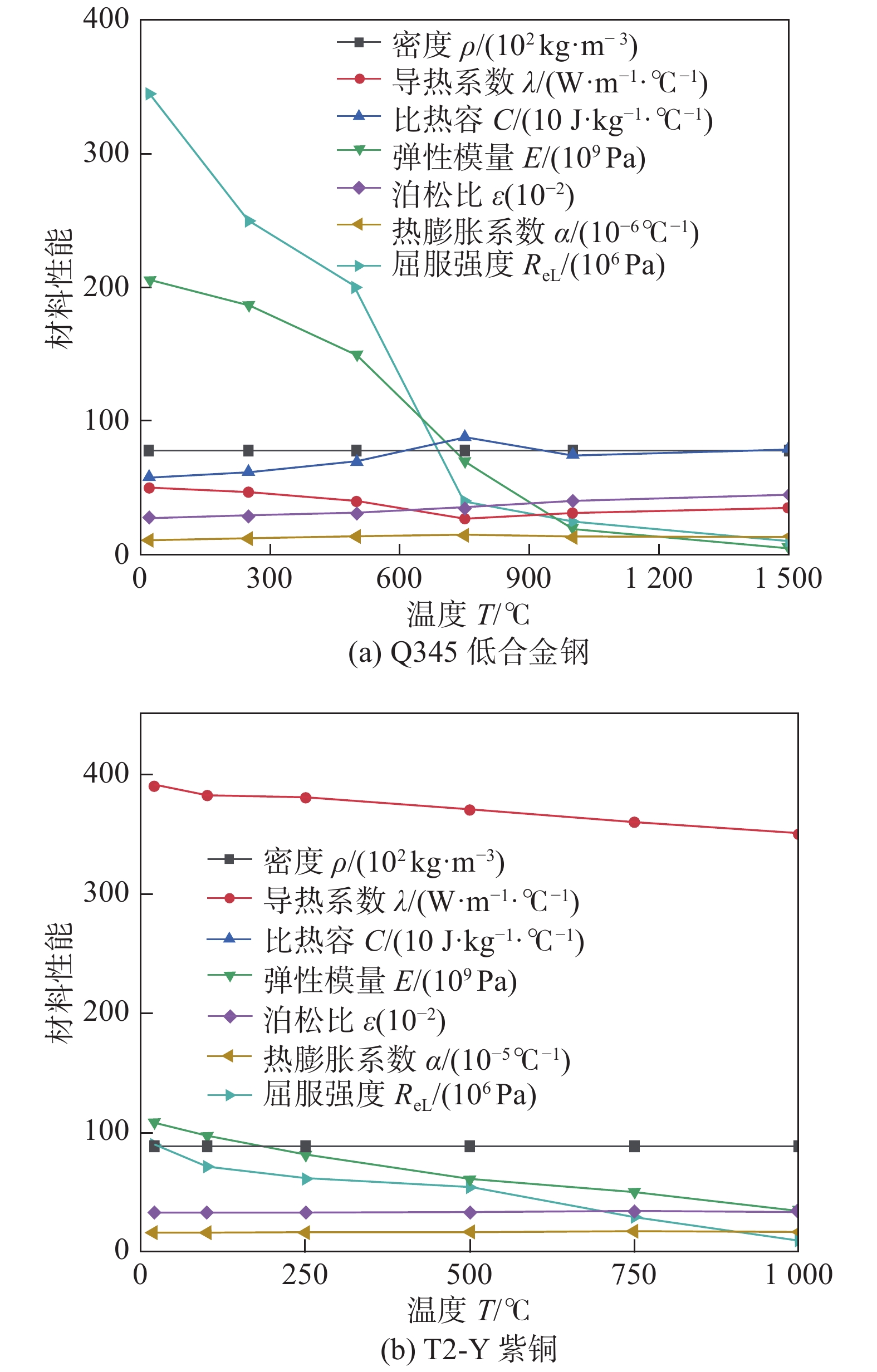
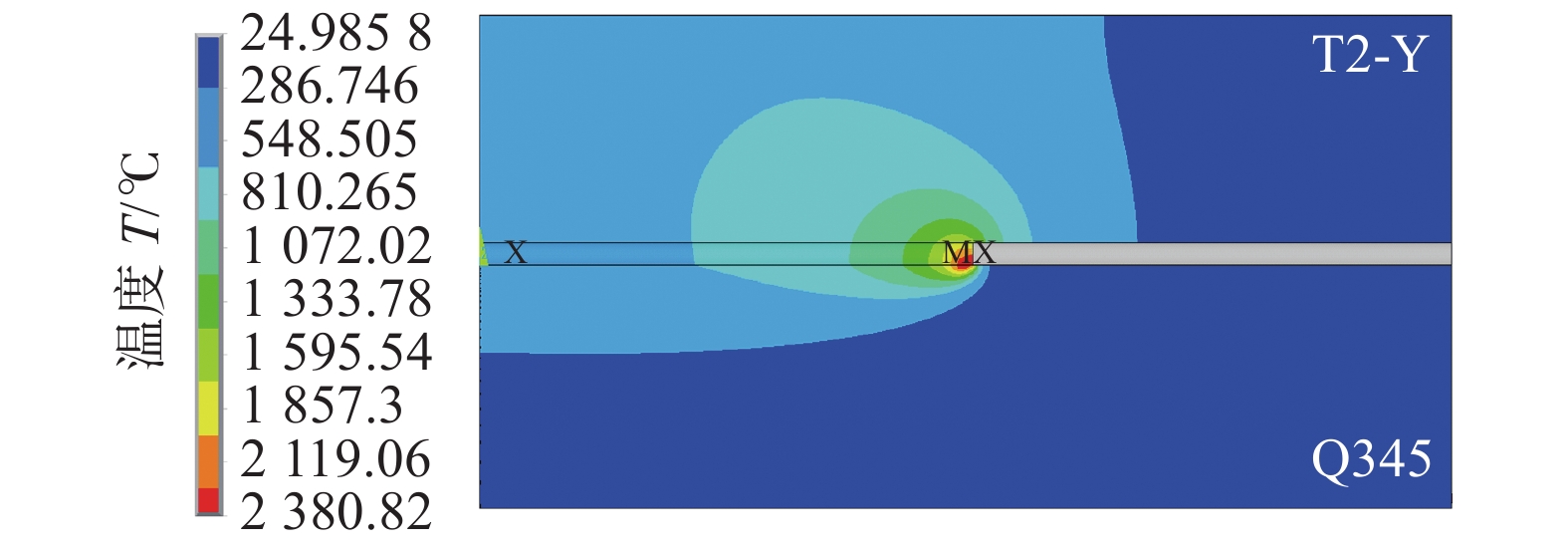
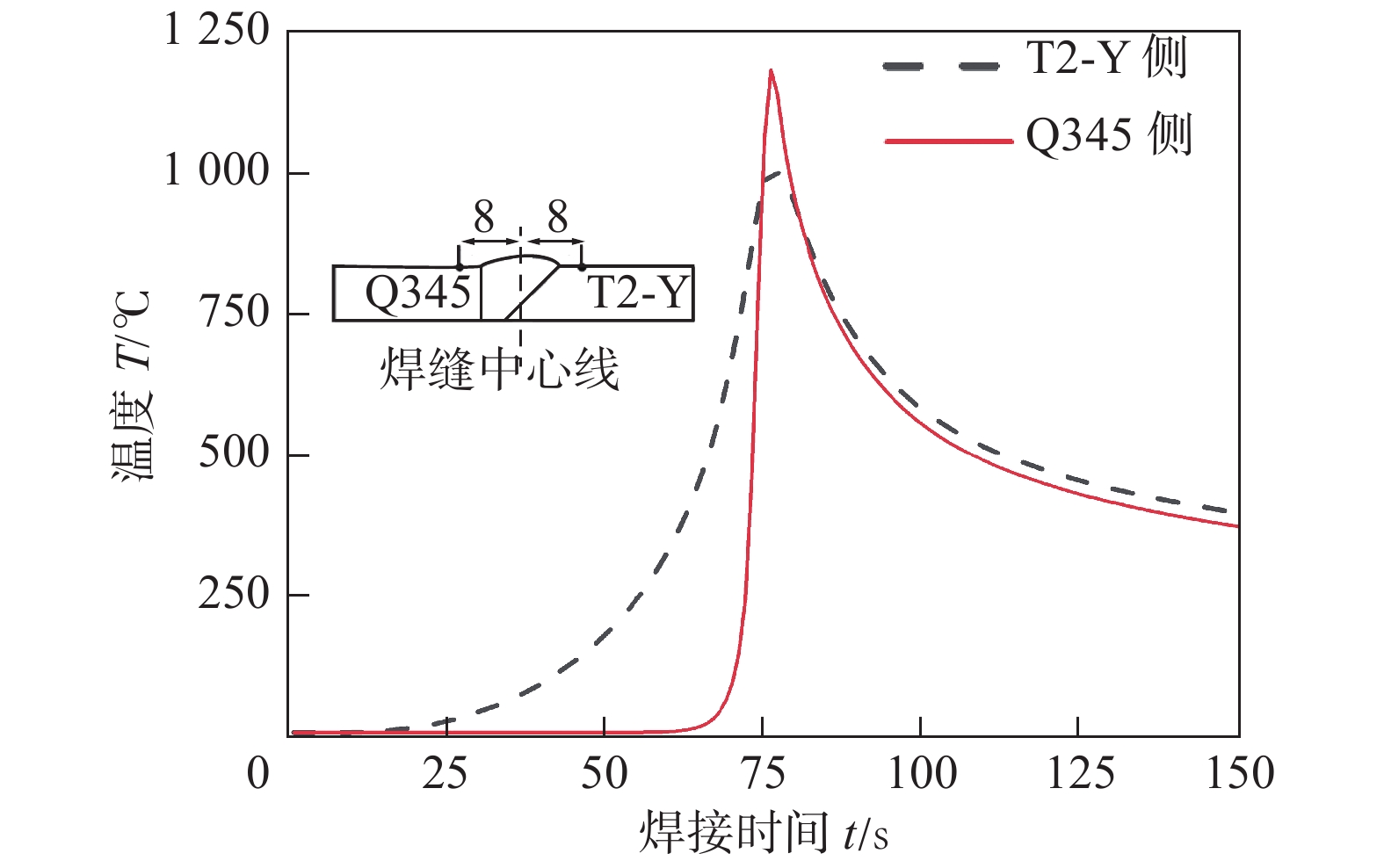
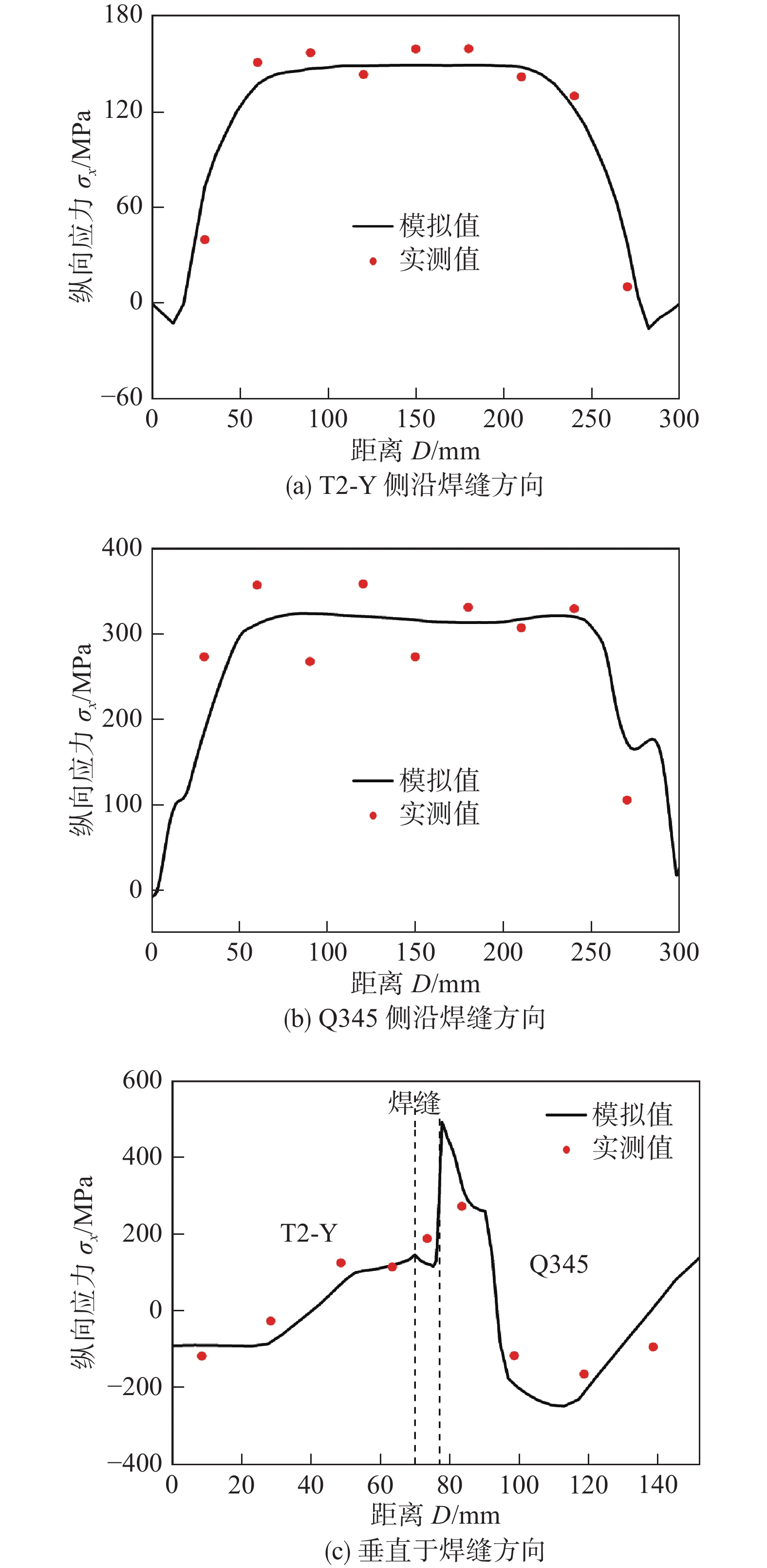
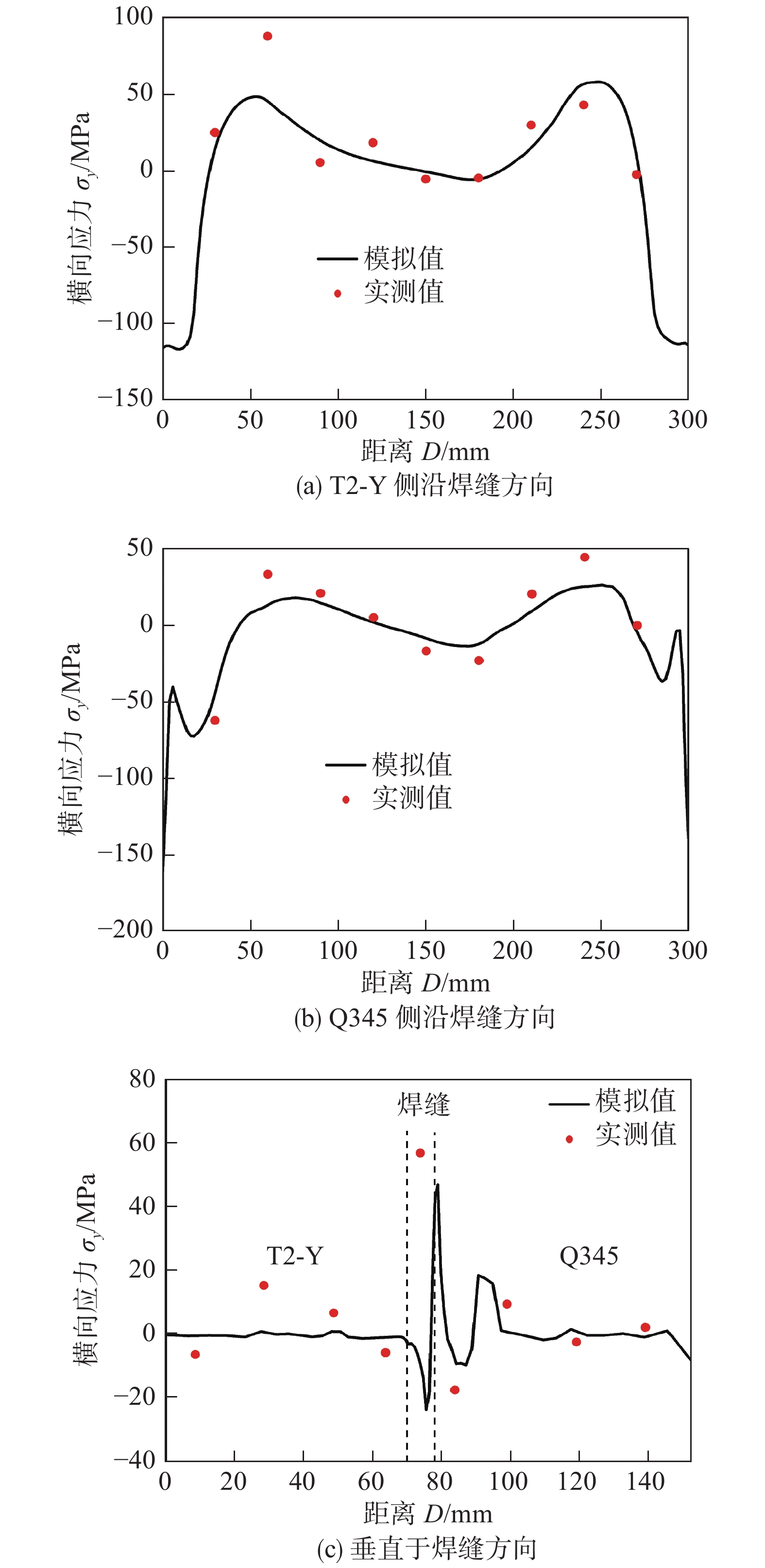
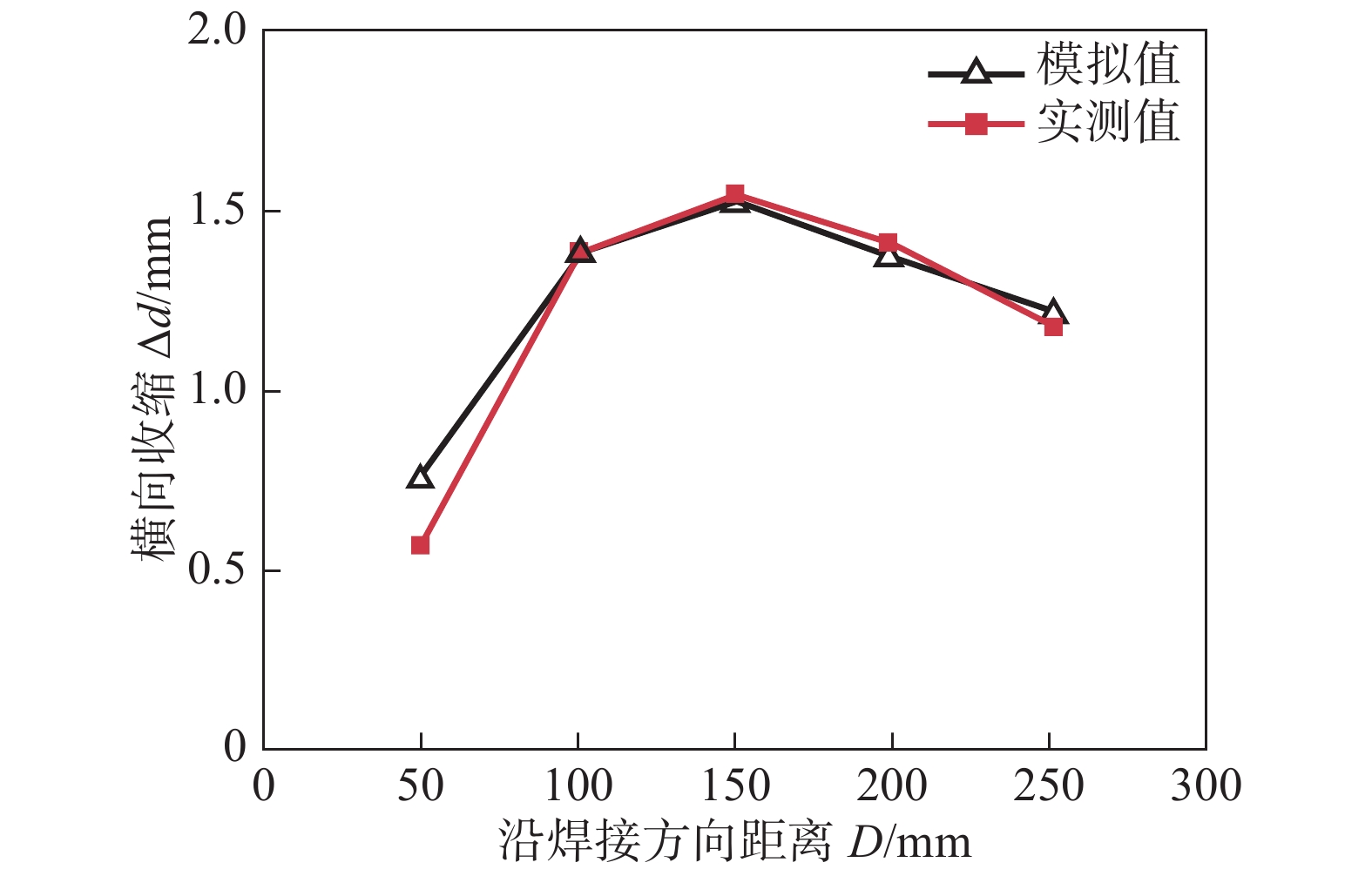
摘要: 利用ANSYS有限元软件基于APDL命令流对T2-Y/Q345异质材料平板对接接头的温度场、残余应力和横向收缩进行数值模拟计算. 同时，对焊接接头的温度、残余应力及横向收缩进行测量. 结果表明，与T2-Y侧相比，Q345侧存在较大的温度梯度. 沿焊缝方向，T2-Y与Q345侧横向应力和纵向应力分别为双驼峰状和帽状分布. 在垂直于焊缝的中央界面的上表面，纵向应力与横向应力在焊缝和热影响区的应力分布均不连续，并在Q345侧存在较大应力梯度. 此外，T2-Y/Q345横向收缩最大位置位于焊缝中间部位，且向两端逐渐减小. 数值模拟结果与试验结果相对比，两者基本吻合，验证了ANSYS有限元计算的可靠性.Abstract: Based on the APDL command flow of ANSYS finite element software to calculate the temperature field, residual stress and lateral shrinkage of the T2-Y/Q345 heterogeneous flat plate butt joint. The temperature, residual stress and lateral shrinkage of the welded joint are measured. The results show that compared with the T2-Y side, there is a larger temperature gradient on the Q345 side. Along the weld direction, the lateral stress and longitudinal stress on the T2-Y and Q345 sides are double hump-shaped and cap-shaped, respectively. On the upper surface of the central interface of the weld, the stress distribution of the longitudinal stress and the lateral stress in the weld and the heat-affected zone are discontinuous, and there is a large stress gradient on the Q345 side. In addition, the maximum lateral shrinkage of T2-Y/Q345 is at the middle part of the welding seam, which gradually decreases towards both ends. The numerical simulation results are basically agreed with the test results, which verifies the reliability of ANSYS finite element calculation.
-
0. 序言
高强钢因具有强度高，延性、韧性好等特点，在船舶、桥梁和钢结构等工程领域中逐渐得到推广应用[1-2]. 钢构件在制造过程中的钢板切割和焊接将不可避免地在构件中产生残余应力和变形，残余应力作为一种重要的初始力学缺陷会使得高强钢压杆受力后某些部位提前进入塑性状态，降低刚度，并影响其稳定承载能力.
近些年，国内外学者在高强钢焊接截面残余应力分布试验研究方面取得了丰硕的成果，但多数针对焊接工字形截面和焊接箱形截面的残余应力分布规律进行研究，并提出了相应的残余应力分布模型[3-6]，专门针对焊接T形截面的研究工作开展的并不多. 熊晓莉等人[7]采用分割法测量了经等离子切割的Q460高强钢板焊接成T形截面的残余应力；Cao等人[8]采用分割法测量经火焰切割的800 MPa高强钢板焊接T形截面的残余应力，探讨了宽厚比的影响，提出两种不同的残余应力分布模型.
基于有限元的数值模拟研究作为一种重要的预测截面残余应力的手段，被越来越多的学者用来预估钢板切割和截面焊接产生的残余应力. 一方面，钢板切割过程的数值模拟研究主要聚焦于切割参数对截面残余应力的影响. Jokiaho等人[9]基于ABAQUS研究了切割速度和预热对低合金耐磨厚钢板火焰切割残余应力分布的影响. 另一方面，截面焊接过程的数值模拟研究主要聚焦于材料属性、约束条件、焊接工艺参数等因素对焊接截面残余应力的影响[10-14]；杜宝帅等人[15]基于ANSYS研究了Q460高强钢多层多道焊平板对接焊的残余应力分布；魏雷等人[16]基于ANSYS研究了Q460高强钢T形接头单边开坡口非对称焊的残余应力分布. 上述研究也是仅考虑了焊接过程产生的残余应力，未考虑钢板切割初始应力对焊接截面残余应力分布的影响. Wei等人[17]基于ANSYS研究了低碳钢平板火焰切割和对接焊连续加工过程后的残余应力分布，研究发现钢板切割初始应力对焊接截面残余应力的影响不容忽视，除此之外还未见有专门针对高强钢切割和截面焊接连续加工过程后截面残余应力分布的相关研究.
采用试验研究与数值模拟相结合的方法，探讨经过钢板切割和截面焊接连续加工过程后的Q460高强钢焊接T形截面纵向残余应力分布. 采用等离子切割方法制作4个Q460高强钢焊接T形截面残余应力试件，并采用分割法测量上述4个试件截面的残余应力大小及分布，借助通用有限元程序ANSYS，运用热-结构耦合分析方法模拟钢板切割及截面焊接的过程，最后将试验结果与数值模拟结果进行对比，验证有限元分析过程的正确性. 基于正确的有限元分析方法，获得更多不同截面尺寸的Q460高强钢焊接T形截面纵向残余应力分布， 基于丰富的试验和数值模拟数据分析截面几何参数对纵向残余应力分布的影响，提出Q460高强钢焊接T形截面纵向残余应力分布模型，为后续钢压杆整体稳定承载力数值模拟研究提供参考.
1. 钢材性能和残余应力测量
1.1 钢材性能
选用8 和12 mm厚度的Q460低合金高强度结构钢板，依照国家标准GB/T 2975《钢及钢产品力学性能试验取样位置及试样制备》要求制备试件，并进行室温单向拉伸试验，测量钢材力学性能参数，具体结果如表1所示. 钢材弹性模量、抗拉强度和屈强比都能满足国家标准GB/T 1591《低合金高强度结构钢》和GB50011《建筑抗震设计规范》要求，能够将表1中数据直接应用于后续研究.
表 1 钢材力学性能Table 1. Test results of steel material property板厚
t/mm弹性模量
E/1011Pa泊松比
v屈服强度
ReL/MPa抗拉强度
Rm/MPa屈强比
R8 1.89 0.275 500 664 0.733 12 1.97 0.285 556 686 0.810 1.2 残余应力测量试件设计及加工
为测量Q460高强钢焊接T形截面的残余应力，采用等离子切割方法获取所需截面尺寸的钢板，切割后钢板采用角焊缝连接，焊接时焊丝采用ER55-D2(直径1.2 mm)，采用自动实心焊丝CO2气体保护焊，其焊接电流为220 A，电弧电压为25 V，焊接速度为250 mm/min，电流极性为直流反接，导电嘴与工件距离为20 mm ± 7 mm，保护气体流量为30 L/min，焊脚尺寸为8 mm. 使用上述方法共设计制作4个焊接T形截面试件，图1为试件截面几何形状示意图，表2为试件截面几何尺寸.
![]()
图 1 试件截面几何形状示意图Figure 1. Schematic diagram of the geometry of the cross-section of the specimen表 2 试件截面几何尺寸Table 2. Sectional dimensions of specimens试件编号 翼缘宽度
B /mm腹板高度
H /mm翼缘厚度
tf /mm腹板厚度
tw /mm翼缘外伸长度
bf /mm宽厚比
bf/tf高厚比
H/twST-1 150 150 8 8 71 8.88 18.75 ST-2 200 200 8 8 96 12.00 25.00 ST-3 150 150 12 12 69 5.75 12.50 ST-4 200 200 12 12 94 7.83 16.67 1.3 残余应力测量方法
分割法是将截面切割分条使其应力释放，测量切割前后条带的长度，并计算截面残余应力，此测量方法可得到较为准确的截面残余应力及分布，具体测量方法及过程详见文献[7].
1.4 残余应力测量结果
截面纵向残余应力测量结果可详见文献[7]，根据测量结果可以看出，Q460高强钢焊接T形截面纵向残余应力有如下特点.
(1) 翼缘残余应力呈对称分布，翼缘焊缝周边区域和外伸端为残余拉应力，翼缘外伸段中部为残余压应力.
(2) 腹板焊缝周边区域和外伸端为残余拉应力，腹板中部为残余压应力.
(3) 截面焊缝处的最大残余拉应力小于钢材实测屈服强度，也小于钢材名义屈服强度.
2. 焊接残余应力数值模拟试验
2.1 有限元模型建立
钢板切割的有限元模型尺寸与试件尺寸一致(图2)，割缝宽度设为1 mm，钢板切割几何形状示意图和切割方向如图2a所示；根据表2中T形截面几何尺寸建立有限元模型，T形截面焊接几何形状示意图和焊接方向如图2b所示；有限元模型网格划分时，为了能够在得到准确计算结果的同时尽量减少计算时间成本，在割缝(焊缝)和热影响区内采用较细的网格划分，距离割缝(焊缝)和热影响区越远，网格划分越稀疏. 图3为钢板切割和T形截面焊接有限元模型的网格划分示意图.
![]()
图 2 钢板切割几何形状和T形截面焊接示意图Figure 2. Schematic diagram of steel plate cutting and T-section welding. (a) steel plate cutting; (b) T-section welding![]()
图 3 有限元模型网格划分示意图Figure 3. Schematic diagram of meshing of finite element model for steel plate cutting and T-section welding. (a) steel plate cutting; (b) T-section welding2.2 材料属性定义
国家标准GB50017—2017《钢结构设计标准》[18]并未对不同温度下的钢材热物理性能参数进行描述，因此参考欧洲标准Eurocode 3 [19]确定相关参数. 密度不随温度变化而变化，取恒定值 ρ = 7 850 kg/m3；泊松比也与温度变化无关，可根据第1.1节材料性能试验测量结果取值，板厚为8 mm的钢材泊松比取恒定值0.275，板厚为12 mm的钢材泊松比取恒定值0.285. 当施加热源时，温度发生变化，钢材的热物理性能和力学性能也会随之改变，变化曲线如图4所示，图4中钢材常温下的屈服强度和弹性模量采用第1.1节材料性能试验的实测值. 后续3.1节将补充板厚为10 mm的有限元模型进行参数分析，考虑到材料性能试验并未测量板厚为10 mm的钢材力学性能参数，因此采用线性内插法得到板厚为10 mm的相关性能参数.
![]()
图 4 钢材热物理性能和力学性能随温度变化Figure 4. Variation curve of thermal properties and mechanical properties of steel with temperature2.3 热源模型选择
现有相关研究中常用的热源模型有高斯热源模型、双椭球热源模型、基于生死单元的焊接热源加载模型及表面高斯热源和生热率组合热源模型等. 基于生死单元的焊接热源加载模型无需构造复杂的热流密度函数，能够在保证计算精度的前提下节省计算时间，因此将采用基于生死单元的焊接热源加载模型对钢板切割过程和T形截面焊接过程进行数值模拟.
钢板切割是将热源施加在割缝处，使割缝处钢材熔融形成熔渣，高速热流使熔渣脱落形成切口. 因此在钢板割缝处施加生热率模拟钢板切割过程，生热率Q的计算公式为
$$Q=\frac{\eta U I}{V_{\mathrm{H}}}$$ (1) 式中：η 为钢板切割时输入热量的效率，取0.35；I为切割电流，取220 A；U为切割电压，取25 V；VH为单位荷载步割缝的体积. 切割速度为250 mm/min，两道割缝之间设置冷却时间为400 s.
截面焊接时热源施加在焊缝处，使焊条熔化与钢材熔融，并冷却后形成焊缝. 可在焊缝处直接施加生热率模拟T形截面焊接过程，此时式(1)中η为焊接时输入热量的效率，取0.85；I为焊接电流，取220 A；U为焊接电压，取25 V；VH为单位荷载步焊缝的体积. 焊接速度为250 mm/min，两道焊缝之间设置冷却时间为400 s， 两道焊缝的焊接参数保持不变，焊接结束后自然冷却至室温. 有限元模型未考虑切割顺序和焊接顺序对残余应力的影响，每个有限元模型均采用同一切割和焊接顺序.
2.4 热分析
钢板切割过程与T形截面焊接过程均采用热-结构耦合分析方法. 在热分析阶段，有限元模型选用能够适用于瞬态热分析的三维热实体单元SOLID70. 为模拟割缝和焊缝与空气对流换热，钢板切割过程和T形截面焊接过程设置对流换热系数为10 W/(m2·K)，环境温度为20 °C.
采用“生死单元”法模拟钢板割缝脱落和T形截面焊缝形成过程. 切割时，对割缝单元依次施加热源，为模拟切缝处熔渣脱落，热源施加完毕后杀死割缝单元；焊接时，先将焊缝单元杀死，模拟焊接准备过程，然后依次激活被杀死单元并施加热源，在焊接过程中，假定焊缝与钢材具有相同的性能参数.
2.5 结构分析
在结构分析阶段，采用ETCHG命令将三维热实体单元SOLID70转化为结构单元SOLID185. 塑性选项使用双线性等向强化模型BISO，定义随温度变化的屈服强度和切线模量，为防止模型发生位移，设置边界条件，钢板切割的边界条件和T形截面焊接的边界条件分别如图2所示. 热分析对应时刻的节点温度在结构分析中作为载荷施加到相应节点进行求解，利用ANSYS后处理命令读取相应位置的纵向残余应力.
2.6 有限元分析结果
为模拟钢板切割和T形截面焊接的连续加工过程，可将钢板切割和T形截面焊接分别得到的纵向残余应力值叠加，即可获得考虑钢板切割初始应力的焊接T形截面纵向残余应力值. 考虑到钢板若在同一位置先切割后焊接，切焊耦合应力场由焊接产生的残余应力决定[20]，因此在焊接T形截面腹板的焊缝处，纵向残余应力由焊接产生的残余应力决定，其它位置的纵向残余应力则为钢板切割和截面焊接叠加后获得. 对残余应力测量试验截面ST-1 ~ ST-4的焊接过程进行数值模拟，分别获取图2b中横截面A-A位置处钢板切割、T形截面焊接和二者叠加的截面纵向残余应力分布，结果汇总于图5，从图5可以得出如下结论.
![]()
图 5 钢板切割、T形截面焊接和切焊叠加的截面纵向残余应力分布Figure 5. Longitudinal residual stress distribution of steel plate cutting, T-section welding and superimposed cutting and welding. (a) ST-1; (b) ST-2; (c) ST-3; (d) ST-4(1) 仅钢板切割时，钢板沿厚度的纵向残余应力分布相同；除切割边缘处为残余拉应力外，钢板其余部分均为残余压应力. 究其原因，钢板切割时基于生死单元的焊接热源模型是均匀施加在割缝处所有单元的，因此沿钢板厚度方向的纵向残余应力不发生改变；近热影响区为纵向残余拉应力，反之则为纵向残余压应力.
(2) 仅T形截面焊接时，焊缝周边区域和腹板外伸端为残余拉应力，翼缘外伸端和腹板中部为残余压应力. 焊接时焊缝处的高温需要通过钢板由近及远耗散，近焊缝区域一般产生残余拉应力，远离焊缝的区域一般为残余压应力，最终达到整个截面上残余应力自平衡状态. 由于焊缝位于翼缘的上表面且与腹板相交位置处，热量沿板厚方向的传导因受到周边高温单元的影响，会出现近焊缝处翼缘和腹板的纵向残余应力沿板厚方向分布不均匀的现象，且板厚越大，这种不均匀现象越明显. 此外还需要注意的是焊缝周边的残余拉应力有时会超过钢材的名义屈服强度，甚至会超过钢材的实测屈服强度，这主要是因为热源集中在焊缝处，导致部分单元提前进入了材料的强化阶段. 然而考虑到超过屈服强度的部分一般在焊接T形截面的近焊缝处，该位置的纵向残余应力其对钢压杆的整体稳定承载力影响不大，因此在后续残余应力分布模型的选取时可偏安全地将焊缝处的最大残余拉应力按钢材的名义屈服强度考虑.
(3) 将钢板切割和T形截面焊接的纵向残余应力进行叠加后，焊缝周边区域、翼缘和腹板外伸端为残余拉应力，翼缘外伸段中部和腹板中部为残余压应力. 与仅考虑T形截面焊接时的纵向残余应力相比，叠加钢板切割加工过程产生的残余应力后，T形截面焊缝周边区域的残余拉应力值略有减少，腹板外伸端的残余拉应力值明显变大，翼缘外伸段中部和腹板中部的残余压应力明显变大，翼缘外伸端的残余应力则由压应力变为了拉应力. 上述变化表明，钢板切割产生的残余应力对Q460高强钢焊接T形截面残余应力分布的影响不能忽略.
2.7 数值模拟结果与试验结果对比
为了验证有限元分析结果的正确性，选取图2b中横截面A-A位置处的数值模拟结果与1.4节中的试验结果进行对比，具体情况如图6所示，从图6可以得出如下结论.
![]()
图 6 截面纵向残余应力分布的试验结果和数值模拟结果对比Figure 6. Comparison of test results and numerical simulation results of longitudinal residual stress distribution in the section. (a) ST-1; (b) ST-2; (c) ST-3; (d) ST-4(1) 焊接T形截面纵向残余应力分布情况的数值模拟结果与试验结果一致，即焊缝周边区域、翼缘和腹板外伸端为残余拉应力，翼缘外伸段中部和腹板中部为残余压应力.
(2) 翼缘焊缝附近的残余拉应力的数值模拟结果与试验结果有差异，但这种差异主要是由有限元方法与试验方法的精度不同所导致的. 有限元方法可以精细地描述焊接热影响区的残余应力分布情况，具体表现为有限元分析所得翼缘上、下表面的残余拉应力明显不同. 主要原因是翼缘上表面在焊缝位置处与腹板相连，焊接时热量输入集中，且降温速度较慢导致该处产生较大的残余拉应力，翼缘下表面相对降温速度较快导致该处产生相对较小的残余拉应力. 用分割法进行残余应力测量时，在翼缘和腹板相交处，切条的难度较大，甚至出现条带上、下表面的残余应力实测值相同的情况，这也是由分割法在焊缝处使用受限决定的，但是翼缘焊缝附近上、下表面残余拉应力平均值的数值模拟结果与试验结果却相当接近.
(3) 腹板外伸端残余拉应力的数值模拟结果与试验结果吻合较好. 考虑到该处的残余拉应力对钢压杆的整体稳定承载力有利，偏于安全地取平均值进行对比. 以ST-3为例，腹板外伸端平均残余拉应力的有限元分析结果为249.99 MPa，试验值为245.96 MPa，前者仅比后者高出1.6%，且未超过钢材名义屈服强度的5%，然而翼缘外伸端残余拉应力的数值模拟结果与试验结果差异较大，这可能与现场试验过程中的约束施加及人工测量的误差有关，但考虑到该处的残余拉应力对钢压杆的整体稳定承载力有利，后续研究过程中可偏安全地在该处取较小的残余拉应力值.
(4) 翼缘外伸段中部和腹板中部的残余压应力的数值模拟结果与试验结果吻合较好. 以模型ST-3为例，翼缘左、右两个外伸段中部的最大残余压应力的有限元分析结果分别为−146.92 和−121.73 MPa，忽略两道焊缝先后焊接次序不同引起翼缘左右两外伸段残余应力的差异，两者的平均值为−134.33 MPa；试验值为−145.20 和−125.60 MPa，平均值为−135.4 MPa；对比有限元分析结果的平均值和试验结果的平均值可知，前者绝对值仅比后者的低0.79%. 同样腹板中部的最大残余压应力的有限元分析结果为−119.09 MPa，试验值为−113.8 MPa，前者绝对值也仅比后者的高4.64%，翼缘和腹板的残余压应力均值的有限元分析结果与试验结果相差均未超过钢材名义屈服强度的5%.
综上所述，翼缘和腹板纵向残余应力分布的数值模拟结果与试验结果总体吻合较好. 虽然在焊缝周边区域，出现了按照两种不同方法获得的残余拉应力不一致的情况，但考虑到这部分区域位于截面中间位置，相应的残余拉应力对焊接T形截面钢压杆整体稳定承载力的影响不大，而对高强钢焊接T形截面钢压杆整体稳定承载力影响较大的翼缘和腹板外伸端残余拉应力、中部残余压应力的数值模拟结果与试验测量值均吻合较好， 因此可以认为提出的有限元分析方法正确合理，可用于后续补充模型的计算，为参数分析提供更多的数据支撑.
3. 参数分析
3.1 补充模型设计
为分析截面几何参数(板件宽厚比和板厚)对Q460高强钢焊接T形截面纵向残余应力的影响，考虑到前述试验及有限元分析获得的残余应力数据有限，特补充设计6种不同截面尺寸的有限元模型，具体截面尺寸如表3所示.
表 3 补充模型的截面几何尺寸Table 3. Section geometry of supplementary models试件编号 翼缘宽度B /mm 腹板高度H /mm 翼缘厚度tf /mm 腹板厚度tw /mm 翼缘外伸长度bf /mm 宽厚比bf/tf 高厚比H/tw STA-1 160 200 8 8 76 9.50 25.00 STA-2 200 160 8 8 96 12.00 20.00 STA-3 200 250 10 10 95 9.50 25.00 STA-4 250 200 10 10 120 12.00 20.00 STA-5 240 300 12 12 114 9.50 25.00 STA-6 300 240 12 12 144 12.00 20.00 3.2 纵向残余应力分布汇总
按照前述的焊接残余应力数值模拟试验过程，对钢板切割和焊接连续加工过程进行数值模拟，获得各截面的纵向残余应力分布，如图7所示.
![]()
图 7 补充模型的纵向残余应力分布Figure 7. Longitudinal residual stress distribution for supplementary model. (a) STA-1; (b) STA-2; (c) STA-3; (d) STA-4; (e) STA-5; (f) STA-6为了便于后续问题研究，将数值模拟得到的Q460高强钢焊接T形截面纵向残余应力分布进行简化，简化的纵向残余应力分布模型如图8所示，图中的各截面纵向残余应力代表值汇总于表4. 图8和表4中，σfrt1为翼缘焊缝区域的最大残余拉应力；σfrt2和σfrt3为翼缘外伸端的最大残余拉应力；σfrc1和σfrc2为翼缘外伸段中部的最大残余压应力；σwrt1为腹板焊缝区域的最大残余拉应力；σwrt2为腹板外伸端的最大残余拉应力；σwrc为腹板中部的最大残余压应力；a ~ j分别表示纵向残余应力各线性分布区段的长度.
![]()
图 8 简化的纵向残余应力分布模型Figure 8. Simplified longitudinal residual stress distribution model表 4 截面纵向残余应力代表值汇总Table 4. Summary of representative values of longitudinal residual stress in section试件编号 翼缘残余拉应力σfrt/MPa 翼缘残余压应力σfrc/MPa 腹板残余拉应力σwrt/MPa 腹板残余压应力
σwrc/MPaσfrt1 σfrt2 σfrt3 σfrc1 σfrc2 σwrt1 σwrt2 ST-1 435.02 111.19 126.68 −277.36 −185.35 510.56 286.67 −137.76 ST-2 466.45 164.86 142.26 −198.02 −161.30 517.54 303.59 −125.75 ST-3 626.32 160.63 154.59 −146.92 −121.73 641.27 249.99 −119.09 ST-4 599.29 100.42 118.24 −96.54 −102.41 633.33 196.28 −79.56 STA-1 464.36 128.40 139.75 −220.25 −178.66 505.68 311.23 −137.05 STA-2 467.69 162.28 139.82 −201.88 −165.17 521.46 282.27 −130.11 STA-3 570.46 215.96 203.89 −144.93 −127.62 552.12 285.08 −125.43 STA-4 538.14 189.74 197.95 −130.99 −130.59 557.56 313.84 −120.43 STA-5 590.75 210.58 207.57 −100.23 −100.09 631.77 325.99 −87.88 STA-6 595.98 273.76 263.69 −80.41 −77.15 637.23 270.93 −87.79 3.3 板件宽厚比对纵向残余应力的影响
图9绘制了板厚为8 和12 mm截面的宽厚比与纵向残余应力之间的关系. 从图中可以看出，翼缘与腹板焊缝周边区域的残余拉应力和翼缘与腹板外伸端残余拉应力均与宽厚比无关；翼缘外伸段中部和腹板中部的残余压应力与宽厚比成反比. 究其原因，翼缘焊缝处的残余拉应力与截面焊接时的热输入能量有关，与板宽厚比无关；翼缘和腹板外伸端为切割边，该处的残余拉应力仅与钢板切割时的热输入能量有关，与宽厚比无关；但因较小宽厚比的板件外伸端更易受到焊接后板件中部产生的残余压应力的影响，因而出现了翼缘外伸端残余拉应力明显与宽厚比成正比、腹板外伸端残余拉应力略微与宽厚比成正比的现象，因此从根本上讲，翼缘和腹板外伸端残余拉应力与宽厚比关系不大. 翼缘外伸段中部和腹板中部的残余压应力主要是由钢板切割和T形截面焊接后钢材的不均匀冷却造成的，热输入能量大小不变，宽厚比越大，残余压应力的分布范围越大，相应的残余压应力越小，当宽厚比较大时(H/tw＞20)，残余压应力的分布范围对应力值的影响不明显.
![]()
图 9 板件宽厚比与纵向残余应力的关系Figure 9. Relationship between width-thickness ratio of plate and longitudinal residual stress. (a) plate thickness is 8 mm; (b) plate thickness is 12 mm3.4 板厚对纵向残余应力的影响
为方便对比，选取表3中宽厚比相同而板厚不同的两组截面，第一组截面为STA-1，STA-3和STA-5，第二组截面STA-2，STA-4和STA-6. 图10为第一组和第二组截面的板厚与纵向残余应力之间的关系，从图中可以看出，焊接工艺参数不变的情况下，翼缘和腹板焊缝周边区域的最大残余拉应力与板厚成正比；翼缘和腹板外伸端的残余拉应力与板厚无关；翼缘外伸段中部和腹板中部的残余压应力与板厚成反比.
![]()
图 10 板厚与纵向残余应力之间的关系Figure 10. Relationship between plate thickness and longitudinal residual stress. (a) the first set of sections; (b) the second set of sections结合图10、图7和表4中的数据可知，板厚越大，虽然翼缘和腹板焊缝周边区域的最大残余拉应力越大，但翼缘和腹板沿板厚方向残余拉应力的分布差异也越大，且部分板厚较大的截面近焊缝位置附近的钢材已进入了强化阶段；考虑到焊缝处的残余拉应力仅与焊接热输入能量有关，在实际取值时可以认为焊缝处的残余拉应力上限为钢材名义屈服强度，与板厚无关；此外随着板厚的增大，翼缘外伸段中部和腹板中部的不均匀冷却速度变慢，最终形成的残余压应力变小.
3.5 截面纵向残余应力的自平衡状态
翼缘、腹板和全截面的不平衡应力σerr计算式为
$$ {\sigma _{{\text{err}}}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{\sigma _{{\text{r}}i}}} \cdot {A_i}}}{A} $$ (2) 式中：n为截面划分单元的数量；σri为各单元对应的残余应力，拉应力取正值，压应力取负值；Ai为各单元的面积；A为截面的总面积.
按照式(2)计算得到各有限元模型的板件不平衡应力，并计算出不平衡应力系数，将两者汇总于图11中. 不平衡应力系数为板件不平衡应力与实测屈服强度的比值. 从图中可以看出，所有模型的各板件不平衡应力系数均未超过5%，可以认为截面纵向残余应力满足自平衡条件.
4. 纵向残余应力分布模型
4.1 分布模型形状
文献[8]提出的800 MPa高强钢焊接T形截面残余应力分布模型，结合前述试验及有限元分析结果，Q460高强钢焊接T形截面纵向残余应力分布模型仍采用图8所示的分布模型形状，翼缘纵向残余应力对称分布(σfrt2 = σfrt3，σfrc1 = σfrc2).
由3.5节分析可知，各板件纵向残余应力满足自平衡条件，因此翼缘和腹板纵向残余应力分别满足如下要求，即
$$ \iint\limits_{{A_{\text{f}}}} {{\sigma _{{\text{fr}}}}{\rm{d}}{A_{\text{f}}} = 0} $$ (3) $$ \iint\limits_{{A_{\text{w}}}} {{\sigma _{{\text{wr}}}}{\rm{d}}{A_{\text{w}}} = 0} $$ (4) 式中：σfr和σwr分别为翼缘和腹板的残余应力；Af和Aw分别为翼缘和腹板的面积.
由图8可知，翼缘和腹板的纵向残余应力分布范围应分别满足下式要求
$$ 2(a+b+c+d+e)=B$$ (5) $$ f+g+h+i+j=H$$ (6) 式中：a ~ e为翼缘纵向残余应力各线性分布区段的长度；f ~ j为腹板纵向残余应力各线性分布区段的长度.
4.2 残余拉应力取值
根据前述分析可知，翼缘和腹板焊缝周边区域的残余拉应力对钢压杆的稳定承载力有利，忽略其沿板厚方向分布的不均匀性以及部分钢材进入强化阶段的影响，可偏安全地取钢材名义屈服强度fy，翼缘残余应力分布范围e取hf + tw/2；腹板残余应力分布范围f取hf.
翼缘和腹板外伸端的残余拉应力与宽厚比无关，考虑到板件外伸端的残余拉应力对钢压杆的整体稳定承载力有利，偏于安全地将取值进行如下简化：翼缘外伸端残余拉应力取0.15 fy，分布范围a取(bf−hf)/10，翼缘残余应力过渡段b的分布范围取(bf−hf)/10；腹板外伸端残余拉应力0.65 fy，分布范围j取(H−hf)/10，腹板残余应力过渡段i的分布范围取(H−hf)/10.
4.3 残余压应力取值
前述分析表明，翼缘和腹板上的最大残余压应力与宽厚比和板厚均成反比，因此对前述试验和有限元分析结果进行非线性拟合，可得翼缘外伸段中部和腹板中部的残余压应力为
$$ \left\{ \begin{gathered} {\sigma _{{\text{frc}}}} = 190 - 720 {({b_{\text{f}}}/{t_{\text{f}}})^{ - 1}} - 2\;600 {t_{\text{f}}}^{ - 1} \\ {\sigma _{{\text{wrc}}}} = 100 - 1\;300 {(H/{t_{\text{w}}})^{ - 1}} - 1\;500 {t_{\text{w}}}^{ - 1} \\ \end{gathered} \right. $$ (7) 式中：σfrc为翼缘外伸段中部的残余压应力；σwrc为腹板中部的残余压应力.
纵向残余应力分布模型中的残余应力分布范围计算公式汇总于表5，残余应力分布模型及相应的计算公式汇总于图12. 根据表5和图12计算可得拟合曲线并将其绘制于图7. 将拟合曲线与图7中的数值模拟结果进行对比，可以看出两者吻合较好. 因此，可将图12中的Q460高强钢焊接T形截面纵向残余应力分布模型应用于后续钢压杆整体稳定承载力研究.
表 5 残余应力分布范围计算公式汇总Table 5. Summary of calculation formulas for residual stress distribution range板件 残余应力各线性分布区段的长度 翼缘 a b c d e (bf-hf)/10 (bf-hf)/10 式(3)和式(5) 式(3)和式(5) hf + tw/2 腹板 f g h i j hf 式(4)和式(6) 式(4)和式(6) (H-hf)/10 (H-hf)/10 ![]()
图 12 Q460高强钢焊接T形截面纵向残余应力分布模型Figure 12. Model of longitudinal residual stress distribution in welded T-section of Q460 high-strength steel5. 结论
(1) 采用分割法测量了高强钢焊接T形截面试件的纵向残余应力，采用等离子切割方法下料并焊接而成的T形截面，其焊缝周边区域、翼缘和腹板外伸端为残余拉应力，翼缘外伸段中部和腹板中部为残余压应力.
(2) 借助通用有限元程序，运用热-结构耦合分析方法模拟钢板切割及截面焊接的过程，获得高强钢焊接T形截面纵向残余应力的数值模拟结果，该结果与试验结果吻合较好，从而验证了有限元分析方法的正确性.
(3) 基于合理的有限元分析方法，改变截面几何参数，获得更多不同截面尺寸的高强钢焊接T形截面的纵向残余应力分布. 以丰富的试验及有限元分析数据为基础，分析截面几何参数对纵向残余应力的影响，得出结论，残余拉应力与板件宽厚比和板厚无关；残余压应力随板件宽厚比和板厚的增大而减小；翼缘、腹板和全截面均满足自平衡条件.
(4) 对试验数据和数值模拟结果进行分段线性拟合，建立Q460高强钢焊接T形截面纵向残余应力分布模型，为后续钢压杆整体稳定承载力研究过程中的初始缺陷取值提供重要参考.
-
![]()
图 2 测试位置(mm)
Figure 2. Position of measuring. (a) transverse shrinkage；(b) residual stress
![]()
图 4 材料性能参数
Figure 4. Material performance parameters. (a) Q345 low alloy steel；(b) T2-Y red copper
![]()
图 7 纵向残余应力
Figure 7. Longitudinal residual stress. (a) T2-Y side along the weld direction；(b) Q345 side along weld direction；(c) perpendicular to weld direction
![]()
图 8 横向残余应力
Figure 8. Transverse residual stress. (a) T2-Y side along the weld direction；(b) Q345 side along weld direction；(c) perpendicular to weld direction
-
[1] Shiri S G, Nazarzadeh M, Sharifitabar M, et al. Gas tungsten arc welding of CP-copper to 304 stainless steel using different filler materials[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(12): 2937 − 2942. doi: 10.1016/S1003-6326(11)61553-7
[2] 杨卫鹏, 李双吉, 朱笑睿, 等. 铜/钢异种金属CMT熔钎焊工艺研究[J]. 焊接, 2015(4): 41 − 45. doi: 10.3969/j.issn.1001-1382.2015.04.008 Yang Weipeng, Li Shuangji, Zhu Xiaorui, et al. CMT brazing-fusion welding process of dissimilar metals of Cu/steel[J]. Welding & Joining, 2015(4): 41 − 45. doi: 10.3969/j.issn.1001-1382.2015.04.008
[3] Zhang H, Ke X J, Jian L Z, et al. Microstructure and mechanical properties investigations of copper-steel composite fabricated by explosive welding[J]. Materials Science & Engineering A, 2018, 731: 278 − 287.
[4] Schasse R, Kannengiesser Th, Kromm A, et al. Residual stresses in repairwelds of high-strength low-alloy steels[J]. Welding in the World, 2015, 59(6): 757 − 765. doi: 10.1007/s40194-015-0257-9
[5] Zhang Min, Zhang Tao, Cai Junqing, et al. Effect of heat treatment on microstucture and properties of explosive welding clad plate of TA1/Q345[J]. China Welding, 2018, 27(1): 26 − 31.
[6] Bajpei T, Chelladurai H, Ansari M Z. Experimental investigation and numerical analyses of residual stresses and distortions in GMA welding of thin dissimilar AA5052-AA6061 plates[J]. Journal of Manufacturing Processes, 2017, 25: 340 − 350. doi: 10.1016/j.jmapro.2016.12.017
[7] 罗海龙, 张敏, 慕二龙, 等. Cu基药芯焊丝TIG焊TA1/Q235B接头微观组织和显微硬度[J]. 焊接学报, 2019, 40(1): 141 − 146. doi: 10.12073/j.hjxb.2019400028 Luo Hailong, Zhang Min, Mu Erlong, et al. Microstructures and microhardness of TA1/Q235B joints welded by TIG with Cu-based flux-cored wire[J]. Journal of Mechanical Engineering, 2019, 40(1): 141 − 146. doi: 10.12073/j.hjxb.2019400028
[8] 张敏, 王晓伟, 韩挺, 等. 中间Cu层对TA1/X65复合板熔焊接头性能的影响[J]. 材料研究学报, 2018, 32(2): 81 − 89. Zhang Min, Wang Xiaowei, Han Ting, et al. Effect of intermediate Cu-layer on mechanical properties of welded joints of TA1/X65 composite plate[J]. Chinese Journal of Materials Research, 2018, 32(2): 81 − 89.
[9] Ming H, Zhang Z, Wang J, et al. Microstructure of a safe-end dissimilar metal weld joint (SA508-52-316L) prepared by narrow-gap GTAW[J]. Materials Characterization, 2017, 123: 233 − 243. doi: 10.1016/j.matchar.2016.11.029
[10] Ramkumar K D, Singh A, Raghuvanshi S, et al. Metallurgical and mechanical characterization of dissimilar welds of austenitic stainless steel and super-duplex stainless steel-a comparative study[J]. Journal of Manufacturing Processes, 2015, 19: 212 − 232. doi: 10.1016/j.jmapro.2015.04.005
[11] Lee C H, Chang K H. Temperature fields and residual stress distributions in dissimilar steel butt welds between carbon and stainless steels[J]. Applied Thermal Engineering, 2012, 45: 33 − 41.
[12] 蔡建鹏, 叶延洪, 张彦杰, 等. 坡口形式对Q345/SUS304异种钢对接接头残余应力和变形的影响[J]. 机械工程学报, 2015, 51(10): 55 − 61. Cai Jianpeng, Ye Yanhong, Zhang Yanjie, et al. Study on influenceof groove type on weldingresidual stress and deformationin Q345/SUS304 dissimilar steel butt-welded joint[J]. Journal of Mechanical Engineering, 2015, 51(10): 55 − 61.
[13] 蔡建鹏, 何静, 张彦杰, 等. Q345/SUS304异种钢对接接头残余应力和变形的分析[J]. 焊接学报, 2016, 37(1): 71 − 75. Cai Jianpeng, He Jing, Zhang Yanjie, et al. Study on welding residual stress and distortion of Q345/SUS304 dissimilar steel buttweld[J]. Transactions of the China Welding Institution, 2016, 37(1): 71 − 75.
[14] 蔡建鹏, 邓德安, 蒋小华, 等. V形坡口和K形坡口Q345/SUS304异种钢对接接头残余应力和变形[J]. 焊接学报, 2016, 37(4): 69 − 72. Cai Jianpeng, Deng Dean, Jiang Xiaohua, et al. Study on weldingresidual stress and distortion in Q345/SUS304 dissimilar steel buttweld of V and K groove type[J]. Transactions of the China Welding Institution, 2016, 37(4): 69 − 72.
[15] 黄本生, 陈权, 杨江, 等. Q345/316L异种钢焊接残余应力与变形数值模拟[J]. 焊接学报, 2019, 40(2): 138 − 144. Huang Bensheng, Chen Quan, Yang Jing, et al. Numerical simulation of welding residual stress anddistortion in Q345/316L dissimilar steel[J]. Transactions of the China Welding Institution, 2019, 40(2): 138 − 144.
[16] Lee C H, Chang K H, Park J U. Three-dimensional finite element analysis of residual stresses in dissimilar steel pipe welds[J]. Nuclear Engineering and Design, 2013, 256: 160 − 168. doi: 10.1016/j.nucengdes.2012.12.016
[17] Xia J, Jin H. Numerical analysis for controlling residual stresses in welding design of dissimilar materials girth joints[J]. International Journal of Precision Engineering and Manufacturing, 2018, 19(1): 57 − 66. doi: 10.1007/s12541-018-0007-1
[18] Goldak J, Chakravarti A, Bibby M. A new finite element model for welding heat sources[J]. Metallurgical Transactions B, 1984, 15(2): 299 − 305. doi: 10.1007/BF02667333
[19] 朱春沅, 李桓, 黄超群, 等. 2219铝合金焊接残余应力分布分析[J]. 焊接学报, 2017, 38(11): 32 − 36. doi: 10.12073/j.hjxb.20160122001 Zhu Chunyuan, Li Huan, Huang Chaoqun, et al. Study on residual stress distribution of 2219 aluminum alloy[J]. Transactions of the China Welding Institution, 2017, 38(11): 32 − 36. doi: 10.12073/j.hjxb.20160122001
[20] Zhu X K, Chao Y J. Effects of temperature-dependent material properties on welding simulation[J]. Computers & Structures, 2002, 80(11): 967 − 976.
[21] Sadeghian M, Shamanian M, Shafyei A. Effect of heat input on microstructure and mechanical properties of dissimilar joints between super duplex stainless steel and high strength low alloy steel[J]. Materials & Design, 2014, 60: 678 − 684.
下载:
计量
- 文章访问数: 817
- HTML全文浏览量: 60
- PDF下载量: 42
