Low-cycle fatigue properties of welded microzones based on the local strain approach
-
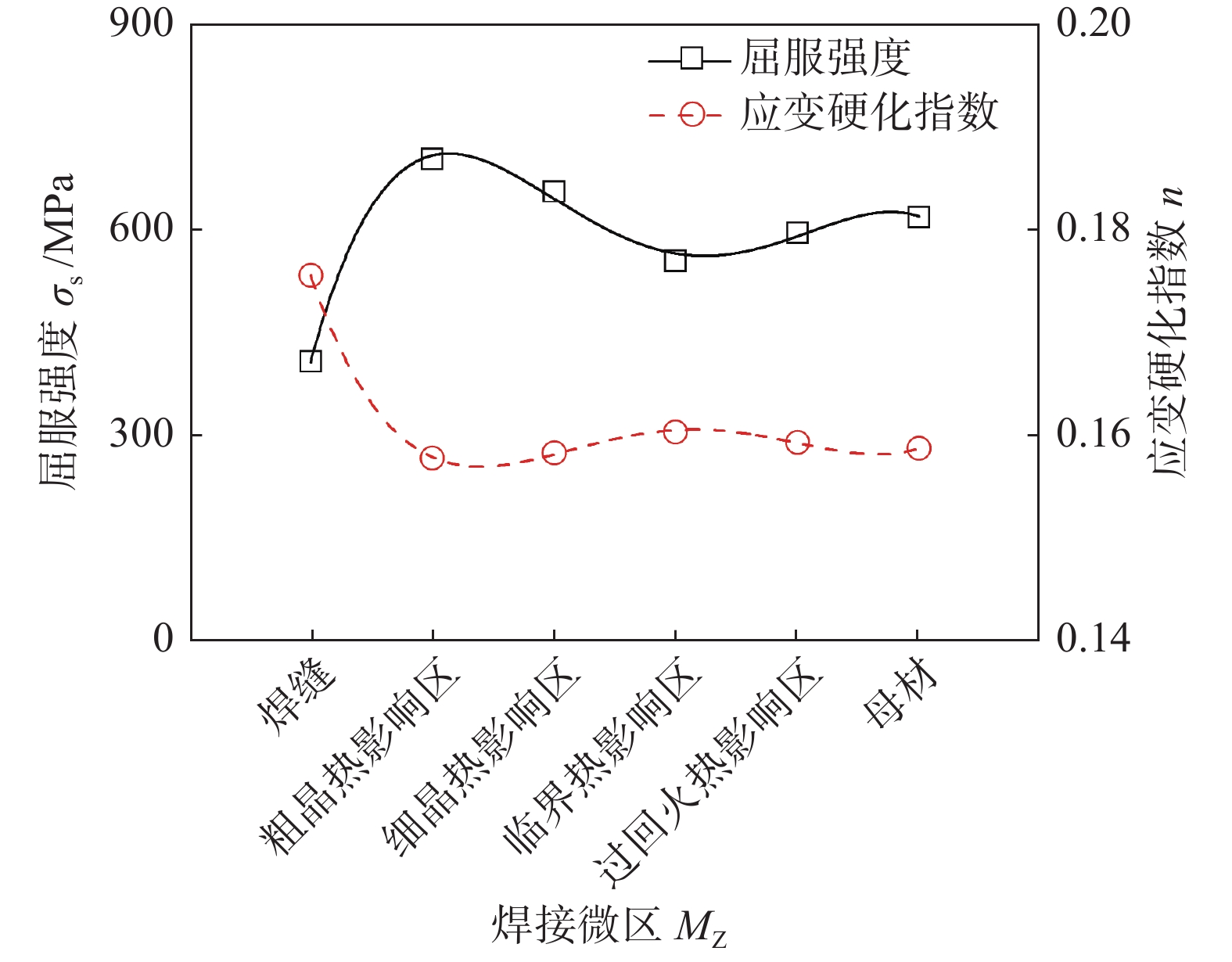
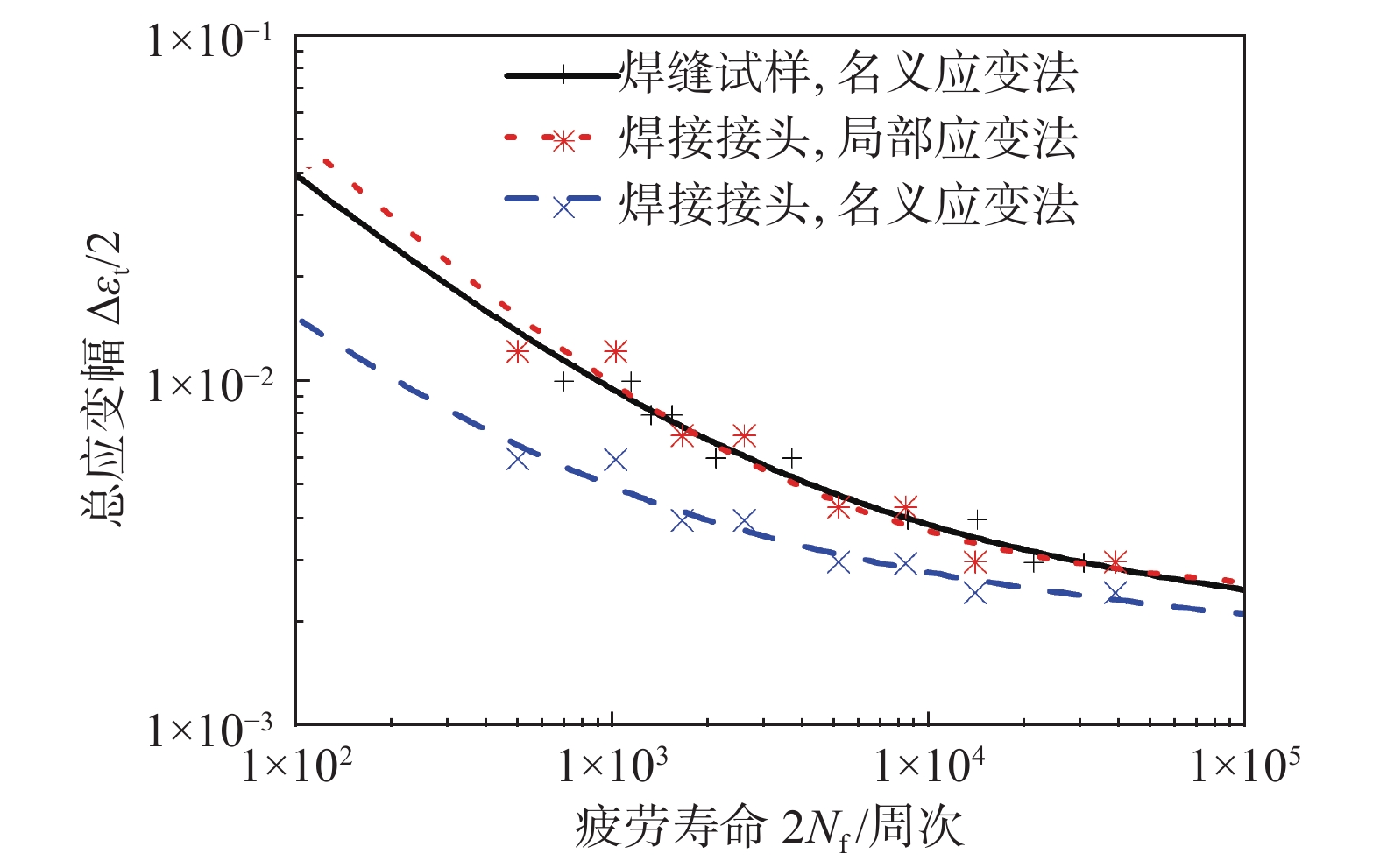
摘要: 针对忽略焊接力学不均匀性的名义应变法评价焊接接头低周疲劳性能不准确的问题,提出一种考虑焊接接头力学不均匀性、基于弹塑性有限元计算的局部应变法,对焊接接头的低周疲劳性能进行准确评价. 通过耐热钢电弧焊接头光滑试样和焊缝光滑试样的低周疲劳试验,以及焊接接头光滑试样在加载过程中的弹塑性有限元计算,采用名义应变法和局部应变法分别对耐热钢电弧焊接头光滑试样进行低周疲劳性能评价. 结果表明,耐热钢电弧焊接头在低周疲劳载荷下断裂于焊缝区域. 采用名义应变法评价该焊接接头时,结果偏保守. 由于局部应变法考虑了焊接接头的力学不均匀性,基于断裂微区的局部应变进行疲劳性能评价,发现采用局部应变法得到的焊接接头应变—寿命曲线与断裂微区焊缝的应变—寿命曲线一致.Abstract: Due to the inaccuracy of the nominal strain approach in evaluating the low-cycle fatigue (LCF) properties of welded joints, a local strain approach considering mechanical heterogeneity of welded joints and based on elastic-plastic finite element analysis was proposed to evaluate the LCF properties of welded joints accurately. The LCF tests of smooth specimens of the welded joint of heat-resistant steel and the weld metal were conducted. The elastic-plastic finite element analysis of the smooth specimens of the welded joints during loading was calculated. The LCF properties of the welded joint were evaluated using the nominal and local strain approach. The results showed that the smooth specimens of the welded joint fractured at the softened weld zone. The LCF properties evaluated by the nominal strain approach were conservative. Since the mechanical heterogeneity of the welded joint was considered by the local strain approach, the LCF properties were evaluated based on the local strain in the fractured microzone. Therefore, the strain−life curve of the welded joint obtained by the local strain approach was close to the strain−life curve of the material of the fractured microzone.
-
0. 序言
疲劳断裂具有瞬时性和不可预测性特点,很多灾难性的事故因为疲劳失效而引起[1]. 焊接结构因其焊缝处的几何、组织不连续性导致的应力集中,使得焊缝处成为焊接结构中薄弱的部位[2-3]. 轨道交通车辆在制造过程中,车体的关键结构许多都由焊接结构组成. 就货车车辆而言,Q460耐候钢焊接接头因其优异的耐候性能、高强度以及较高的塑韧性而广泛地应用于铁路货车. 然而焊接结构在服役过程中会承受许多循环往复的载荷,从而导致疲劳失效的发生[4]. 因此,如何能准确地评估其焊接结构的疲劳强度,使其在规定的寿命内保持稳定的强度成为业界关注的主要问题.
目前,结构疲劳强度的评估方法主要为传统的升降法,该方法是通过获得多组升降子样对的平均值来确定给定寿命下的疲劳强度,但是局限性在于对试件的需求量较大. 因此,对于试件数量有限的样本,采用升降法得到的结果可能与实际值出入偏大.
近年来,许多热像法被用于进行疲劳强度的评估,其主要是借助热电偶[1]、热敏电阻[2]以及红外热像仪[5-8]等接触式或非接触式测温装置实时测定记录试件表面的温度变化. 然后,得到不同载荷下的稳定温升阶段的温升增量数据,绘制其增量和载荷的曲线. 通过拟合数据得到两条斜率明显不同的直线,并将两直线交点的横坐标作为疲劳强度的预测值. 该方法首先被Fargione等人[9]和Luong等人[10-11]提出,然后被国内外相关学者广泛地应用于疲劳极限的评估. 基于该方法进行疲劳强度预测的相关工作见文献[11-14].
热像法是基于疲劳温升增量随载荷增加存在一个阀值的假设,即当载荷高于疲劳强度,稳定阶段的温升步长随载荷增加较快,而当载荷低于疲劳强度,则增加较慢. 因此,Guo等人[15-17]受这一假设的启发,认为能量耗散也存在一个阀值,而该阀值也可以用于预测疲劳强度. 该方法的优势在于能够揭示疲劳温升背后的能量机理,揭示不可逆微观塑形变形是疲劳损伤的根本原因. 此后,Guo等人[15]借助于双线法预测疲劳极限,发展了基于能量耗散的双线法评估疲劳极限,并且试验结果得到了较好的验证. 然而,双线法是需要找到两条斜率相差较大的拟合曲线,但是很多情况下,拟合曲线往往呈现非线性行为[12],而此时借助双线法则难以实现疲劳强度的快速预测. 不过值得注意的是,双线法本质上是将斜率转折点作为疲劳强度的预测阀值. 因此,受这一点启发,一种更加普适的方法可能被提出.
基于稳定温升阶段的能量耗散,建立一种将能量耗散作为损伤指标的焊接接头疲劳强度评估方法(最大斜率法). 借助红外热像仪实时监测试件表面疲劳温升,获得稳定温升阶段的能量耗散,并将该参量作为疲劳强度评估的指标,以期实现快速、精确的疲劳强度预测.
1. 能量耗散模型建立
疲劳是一个不可逆能量耗散逐渐增加的过程,而试件表面温度升高是能量耗散存在的一个重要表现. 为了描述疲劳过程中的实时能量耗散情况,根据连续介质力学的观点,高周疲劳过程中的能量耗散过程可以认为是一个准静态不可逆热力学过程[16-17]. 因此,对于高周疲劳过程中的任意周次,试件标距内的能量守恒关系式可以表示为
$$ \rho C\dot T - {\rm{div}}(k{\rm{grad}}T) = d + {s_{{\rm{the}}}} + {s_{{\rm{ic}}}} + {r_{\rm{e}}} $$ (1) 式中:ρ是材料的密度;C是材料的比热容;
$\dot T$ 是着温度变化率;$\;\rho C\dot T$ 代表着储能速率;div(kgradT)是由热传导引起的能量损失率;d是能量耗散;sthe,sic和re分别代表着热弹性源,由内摩擦引起的热源以及外部体积热源.疲劳温升的过程总结为典型的三段论[12]:第一阶段,温度迅速升高;第二阶段,温升趋于稳定和平缓(黑色虚线框内的蓝色波动线表示由热弹性引起的温度波动);第三阶段,裂纹迅速扩展时的温度急剧陡升(图1). 如前所述,疲劳过程中的任一周次内的能量守恒关系式可以表示为式(1),而由热弹性、内摩擦以及外部引起的热源是几乎可以忽略不计的[16-18]. 因此,式(1)可以简化为
$$ \rho C {\frac{{\partial \theta (x,t)}}{{\partial t}}} - {\rm{div}}\left\{ {\frac{{{\partial ^2}\theta (x,t)}}{{\partial {x^2}}}} \right\} = d $$ (2) 式中:
$\dfrac{{\partial \theta (x,t)}}{{\partial t}}$ 是温度对时间的偏导,$\rho C\dfrac{{\partial \theta (x,t)}}{{\partial t}}$ 代表着储能速率;${\rm{ div}}\left\{ {\dfrac{{{\partial ^2}\theta (x,t)}}{{\partial {x^2}}}} \right\}$ 是被热传导引起的热损;d是能量耗散. 这里,值得说明的是,对于一个疲劳试件来说,因试件标距部分长度远大于试件的宽度和厚度. 因此,式(1)和式(2)经仅考虑垂直于焊缝方向的温度场[19],见图2. 对于式(2)中的d可以表示为[19]$$ d= \frac{1}{l}\int\limits_{\frac{{ - l}}{2}}^{\frac{l}{2}} {\frac{{\theta (x)}}{R}{\rm{d}}x} $$ (3) 式中:θ(x)是稳定阶段的沿x方向的试件表面温度(这里取加载前结束10 s位置处的温度分布);R是热阻;l是试件标距部分长度. 因红外热像仪采集的热像数据沿标距方向是离散的,即不能满足式(3)的积分形式. 因此,对于离散的热像数据,可以用式(4)代替式(3)计算能量耗散.
$$ {\rm{d}}(t) = \frac{{\displaystyle\sum\limits_{i = 1}^n {\theta ({x_i})} }}{{nR}}{\rm{ }}(1 \leqslant i \leqslant n) $$ (4) 式中:n是试件标距范围内x轴方向的离散热点总数.
根据文献[19],式(4)中的热阻R可以表示为
$$ R = \frac{{{w_0}{v_0}}}{{2({w_0} + {v_0})({h_{\rm{r}}} + {h_{\rm{c}}})}} $$ (5) 式中:v0和w0分别是试件标距部分的宽度和厚度;hr是热辐射系数;hc热对流系数;hr和hc可以分别表示为
$$ {h_{\rm{r}}} = \varepsilon \sigma ({T^2} + {T_0}^2)(T + {T_0}) $$ (6) 式中:ε为热发射率;σ为斯特藩玻尔兹曼常数;T为试件中心位置处的温度值;T0为试件初始温度值.
$$ {h_{\rm{c}}} = 0.59{k_{\rm{a}}}{\left(\frac{{0.71g\beta \Delta T}}{{{v^2}}}\right)^{\tfrac{1}{4}}}{l^{\tfrac{{ - 1}}{2}}} $$ (7) 式中:ka是热传导因数;v是黏性系数;g是重力加速度;β是体积扩散系数,其计算公式为
$$ \beta = \frac{1}{{{T_{\rm{f}}}}} $$ (8) 式中:Tf等于
$\dfrac{1}{2}({T_{\rm{w}}} + {T_{\rm{r}}})$ ,Tw和Tr分别是试件的表面温度和室温. 因此,能量耗散可以通过式(4)计算得到.2. 疲劳强度预测模型
如第1节所述,稳定温升阶段的能量耗散可以通过式(4)计算得到. Guo等人[15]认为稳定温升阶段的能量耗散会随着载荷的增加存在一个阀值,即当载荷高于疲劳强度时,能量耗散随载荷上升增加的速率较快;当载荷低于疲劳强度时,则增加较慢. 因此,能量耗散在随载荷增加过程中,呈现一种双线性行为,如图3a所示. 图3a描述的是一种双线法,该方法将两条拟合曲线的交点的横坐标作为疲劳强度的预测值,且已经被许多相关工作验证[20-25]. 然而,值得指出的是,能量耗散随载荷的变化情况有时会呈现非线性行为[12]或无法找到明显的两条斜率不同的拟合直线. 因此,这种情况下,采用双线法无法得到疲劳强度的预测值. 不过双线法的核心点是能量耗散随载荷增加的斜率存在转折点. 因此,受这一点以及文献[20]启发,对于呈现非线性行为或无法实现双线性拟合的数据,可以发展一种新的方法来评估该种情况下的疲劳强度,如图3b所示,命名为最大斜率法.
具体来说,该方法将所有数据点按载荷从小到大的顺序,依次命名为P1,P2,···,Pi,Pi+1,···,Pn相邻两点之间的斜率可以表示为
$$ {S_{i + 1}} = \frac{{{d_{i + 1}} - {d_i}}}{{{\sigma _{ai + 1}} - {\sigma _{ai}}}}{\rm{ }}(1 \leqslant i \leqslant n) $$ (9) 式中:n是数据点数;Si+1是Pi,Pi+1两点之间的斜率值;di是Pi点的能量耗散值;σai是Pi点的应力幅值.
如图3b所示,相邻两点的斜率Si+1可以通过式(9)得到. 然后,为确定疲劳强度,将相邻两斜率的差值的最大绝对值对应点的横坐标作为疲劳强度的预测值,即
$$ {\beta _{i + 1}} = \max \left\{ {\left| {{S_{i + 1}} - {S_i}} \right|} \right\} $$ (10) 至此,式(10)描述了一种针对数据分布呈现非线性行为或无法实现双线性拟合的疲劳强度评估新模型. 其优势在于能够实现一种更为普适的评估方法,不仅适用于双线性情况,而且还适用于其他情况下的疲劳强度评估. 双线法可以看作为最大斜率法的一个特例,即最大斜率转折点出现在两直线的交点处.
3. 试验方法
3.1 试验试件和材料
疲劳试验采用铁路货车Q460耐候钢焊接的对接接头,其力学性能如表1所示. 采用MIG焊完成Q460对接板焊接,其焊接电压为26 V,焊接电流220 A,焊接速度为6.5 mm/s,为单层单道焊. 保护气体为氩气,为保证Q460对接板的充分熔透,坡口角度为55°,钝边取1 mm,焊后自然冷却到室温状态. 焊后冷却试板经线切割工艺完成试件加工,试件尺寸如图4所示,其板厚为5 mm.
表 1 Q460对接接头力学性能Table 1. Mechanical properties of Q460 butt joints屈服强度
ReL/MPa抗拉强度
Rm/MPa断后伸长率
A(%)冲击吸收能量
Akv/J659.4 737.9 21.5 56(−40 ℃) 3.2 疲劳试验及温升测量
PLG-200疲劳试验机型如图5所示,其可加载最大载荷值为200 kN,加载误差为±1%. 采用轴向脉动拉伸的加载方式,载荷按照正弦曲线进行变化,应力比为0.1,加载频率为112 Hz,指定疲劳循环次数为2 × 106次. 采用板厚为5 mm的Q460对接接头进行疲劳试验,具体的实现步骤为:在装夹试件之前,载荷清零;使用夹块夹紧试件两端部;设置动态幅值,平均载荷以及应力比;加载,开始试验. 试验过程中采用红外热像仪实时监测试件表面温升.
采用Fluke Ti450红外热像仪对试件表面温度进行同步实时监测. 为准确测量试件表面温度,应在试件表面喷一层黑色哑光漆来提升表面热发射率. 红外热像仪取样次数为每3秒一次,并将热图进行实时传输和存储. 借助Smartview红外热像图处理分析软件,进行热像数据的处理和分析,提取疲劳试验全过程的疲劳温升数据.
4. 试验结果
4.1 能量耗散计算
疲劳过程伴随着不可逆的能量耗散,这种耗散是以试件表面温度升高的形式而展现的. 因此,通过采用热像设备记录表面温升,并建立相应的能量耗散模型,可以得到不同载荷水平下稳定温升阶段的能量耗散. 如第1节所述,稳定温升阶段某一时刻的能量耗散值可以通过式(4)的计算得到. 因此,主要工作可以总结为:基于Smartview分析热像图得到温度数据;通过查表[23]和线性拟合,得到ka和v的估计值;计算热辐射系数hr和热对流系数hc借助式(6)和式(7);估计热阻R可通过式(5).
值得指出的是,对于在指定循环次数内失效的试件,取第二阶段结束前10秒位置处的能量耗散值进行计算;对于在指定循环次数内未出现失效的试件,取试验停止前10秒位置处的能量耗散值进行计算. 因此,不同载荷水平下,其相关参数和能量耗散计算值如表2所示. 计算能量耗散采用的应力幅值分别为148.5,135,130.5,126,121.5,117,112.5和108 MPa. 其中工作在应力幅值为148.5,135,130.5,126,121.5和117 MPa的试件在指定循环周次内失效,而工作在112.5 MPa和108 MPa的两个试件在指定的周次内未失效.
表 2 能量耗散和相关参数计算值Table 2. Calculation of energy dissipation and relevant parameters应力幅σa/MPa 热传导因数ka/(10−2 mW·mm·K−1) 黏性系数v/(mm2·K−1) 热阻R/(10−2 (mm3·K·m−1 W−1)) 能量耗散d/(mW·mm−3) 148.5 2.46 15.7 2.00 1.52 135.0 2.46 15.6 2.10 1.44 130.5 2.45 15.6 2.12 1.42 126.0 2.45 15.6 2.12 1.42 121.5 2.45 15.6 2.14 1.41 117.0 2.44 15.5 2.21 1.37 112.5 2.44 15.5 2.22 1.36 108.0 2.44 15.5 2.38 1.26 表2记录了不同载荷下的稳定温升阶段的能量耗散值以及相关参数的计算,可以看出,能量耗散随着载荷的增加而逐渐增加,这与Yang等人[19]所述一致. 因此,建立载荷和能量耗散的关系图,并基于提出的模型可以实现疲劳强度的预测与评估.
4.2 疲劳强度预测
如前所述,给定循环次数下的疲劳强度评估可以通过双线法和最大斜率法,双线法为传统的红外热像法,通过将不同载荷下的热像数据拟合为两条斜率明显不同的直线,然后,将两直线交点的横坐标作为疲劳强度的估计值. 受双线法的启发,发展了一种最大斜率法,并将所有数据点按载荷从小到大的顺序(即将应力幅108,112.5,117,121.5,126,130.5,135和148.5 MPa分别记第1,2,···,i,i+1,···n级载荷),依次命名为P1,P2,···,Pi,Pi+1,···,Pn,并依次计算P1P2,P2P3,···,PiPi+1以Pn−1Pn (图3b)等相邻两点之间的斜率,根据式(9)将斜率值依次命名为S2,S3,···,Si+1,···,Sn并将
$\;{\beta _{i + 1}} = \max \left\{ {\left| {{S_{i + 1}} - {S_i}} \right|} \right\}$ 对应的应力幅值作为疲劳强度的预测值,其优势在于不仅适用于双线性行为,而且还适用于其它非线性行为,具有较好的普适性.图6a表示基于双线法得到的疲劳强度估计值,其中,拟合曲线1和拟合曲线2的函数表达式分别为
$$ {y_1} = 0.020\;72x - 0.974\;31 $$ (11) $$ {y_2} = 0.004\;23x + 0.881\;46 $$ (12) 联立式(11)和式(12),将两式交点的横坐标作为疲劳强度估计值,其值为112.54 MPa (图6b). 对于拟合曲线1,两个点用于拟合该条曲线,其决定系数R平方为1;而对于拟合曲线2,6个点用于该条曲线的拟合,其决定系数R平方为0.939 01 (大于0.8),这表明拟合效果较好.
图6b表示疲劳强度预测值通过提出的最大斜率法得出,从图中可以看出,β2为最大的βi+1,即相邻两斜率差值的最大绝对值. 因为i+1等于2,故取112.5 MPa作为疲劳强度的估计值. 其值与经双线法得到的疲劳强度值几乎一致,从而验证了模型的准确性.
上述疲劳强度经双线法和最大斜率法实现了较好的评估,二者预测值几乎相等,这表明双线法可以作为最大斜率法的一个特例. 为研究其疲劳强度预测精度,还需将预测结果与升降法疲劳试验的计算结果进行对比.
图7为采用升降法进行的给定寿命下的疲劳强度试验结果,根据国家标准GB/T 24176—2009《金属材料 疲劳试验 数据统计方案与分析方法》取4个字样对进行给定寿命下的条件疲劳强度计算. 因此,板厚为5 mm的Q460对接接头在给定2 × 106次循环次数下的疲劳强度值,如式(13)所示.
$$\begin{split} {\sigma _{0.1}} &= \frac{{\displaystyle\sum\limits_{i = 1}^8 {{\sigma _i}} }}{8} = \frac{{(126\times 2 + 121.5\times 4 + 117 \times 2 )}}{8} \\ &=121.5 \;{\rm{MPa}} \end{split} $$ (13) 表3为基于双线法、最大斜率法以及升降法得到的疲劳强度预测值. 可以看出,通过最大斜率法(ZM)获得的疲劳强度与由双线法和升降法得到的疲劳强度估计值的误差分别为0.04%和7.40%,这表明该方法有着较高的精度,可以实现较为精确的疲劳强度预测.
表 3 基于不同方法的疲劳强度值Table 3. Fatigue strength based on different methods双线法
疲劳强度
RBM/MPa最大斜率法
疲劳强度
RZM/MPa升降法
疲劳强度
RSM/MPa$\left| {\dfrac{ { {R_{ {\rm{ZM} } } } - {R_{ {\rm{SM} } } } } }{ { {R_{ {\rm{SM} } } } } } } \right|$ $\left| {\dfrac{ { {R_{ {\rm{ZM} } } } - {R_{ {\rm{BM} } } } } }{ { {R_{ {\rm{BM} } } } } } } \right|$ 112.54 112.5 121.5 7.40% 0.04% 5. 结 论
(1)基于能量耗散模型得到了不同载荷等级下的能量耗散值,然后利用最大斜率法进行了给定寿命下的疲劳强度评估.
(2)通过最大斜率法得到的疲劳强度与由双线法和升降法得到的疲劳强度预测值的误差分别为0.04%和7.40%,验证了模型的准确性,从而为实现实时、快速测定焊接接头疲劳强度提供了一种新思路.
-
表 1 材料的化学成分(质量分数,%)
Table 1 Chemical compositions of materials
材料 C Mn Cr Co W V Mo Ni Nb N Fe S P Si 母材 0.11 0.08 9.82 3.06 1.72 0.20 0.71 0.36 0.08 0.03 余量 — — — 熔敷金属 0.05 3.00 16.50 — — — 0.30 余量 2.60 — 6.50 0.01 0.01 0.40 表 2 焊接工艺参数
Table 2 Welding process parameters
焊接方法 焊接电流I/A 电弧电压U/V 焊接速度v/(mm·min−1) 钨极氩弧焊 115 11 ~ 13 80 ~ 110 焊条电弧焊 150 28 ~ 31 250 ~ 280 -
[1] Zamzami A I, Susmel L. On the accuracy of nominal, structural, and local stress based approaches in designing aluminium welded joints against fatigue[J]. International Journal of Fatigue, 2017, 101: 137 − 158. doi: 10.1016/j.ijfatigue.2016.11.002
[2] 杨鑫华, 孙屹博, 邹丽. 网格不敏感结构应力的焊接疲劳数据分布[J]. 焊接学报, 2015, 36(2): 11 − 14. Yang Xinhua. , Sun Yibo, Zou Li. Data distribution in welding fatigue analysis based on mesh-insensitive structural stress[J]. Transactions of the China Welding Institution, 2015, 36(2): 11 − 14.
[3] Pei X, Dong P. An analytically formulated structural strain method for fatigue evaluation of welded components incorporating nonlinear hardening effects[J]. Fatigue & Fracture of Engineering Materials & Structures, 2019, 42(1): 239 − 255.
[4] Littlewood P, Wilkinson A. Local deformation patterns in Ti-6Al-4V under tensile, fatigue and dwell fatigue loading[J]. International Journal of Fatigue, 2012, 43: 111 − 119. doi: 10.1016/j.ijfatigue.2012.03.001
[5] Hanji T, Park J, Tateishi K. Low cycle fatigue assessments of corner welded joints based on local strain approach[J]. International Journal of Steel Structures, 2014, 14(3): 579 − 587. doi: 10.1007/s13296-014-3015-8
[6] Xu Z, Zhang J, Wang W, et al. Low-cycle fatigue properties of Ti6Al4V laser-welded joints based on a local strain approach[J]. Journal of Materials Engineering and Performance, 2021, 30(4): 2772 − 2780. doi: 10.1007/s11665-021-05540-7
[7] 张建勋, 徐甄真, 白嘉瑜, 等. 一种焊接接头的低周疲劳性能评价方法: 中国, 202010042994.9[P]. 2021-01-19. Zhang Jianxun, Xu Zhenzhen, Bai Jiayu, et al. An evaluation method for the low cycle fatigue properties of welded joints: China, 202010042994.9[P]. 2021-01-19.
[8] Zhang P, Li S, Zhang Z. General relationship between strength and hardness[J]. Materials Science & Engineering: A, 2011, 529: 62 − 73. doi: 10.1016/j.msea.2011.08.061
[9] Cahoon J, Broughton W, Kutzak A. The determination of yield strength from hardness measurements[J]. Metallurgical Transactions, 1971, 2(7): 1979 − 1983. doi: 10.1007/BF02913433
-
期刊类型引用(5)
1. 庞嘉尧,程伟. 铝合金搅拌摩擦焊接头疲劳性能研究进展. 兵器材料科学与工程. 2025(01): 164-175 .  百度学术
百度学术
2. 经中涛,丁洁琼,周禄军,李树栋. 某地铁司机室型材内部筋方向对焊接变形影响的工艺研究. 机车车辆工艺. 2025(01): 21-24 .  百度学术
百度学术
3. 翟明,宋宏图,石磊,任金雷,李政,石孟雷. 搅拌摩擦焊在轨道交通领域的应用现状与发展前景. 金属加工(热加工). 2024(01): 1-7 .  百度学术
百度学术
4. 田春雨,李洪林,周金旭,叶树茂,金鑫,邓鑫. 6005A-T6铝合金搭接接头激光焊工艺研究. 有色金属加工. 2024(06): 31-35 .  百度学术
百度学术
5. 陈文雅,宋娓娓,汪洪峰. 聚丙烯塑料搅拌摩擦连接区性能分析. 塑料科技. 2024(12): 93-96 .  百度学术
百度学术
其他类型引用(2)












 下载:
下载: