Real-time detection of pseudo-defect in laser welding of power battery tabs based on photoelectric coaxial sensing
-
摘要:
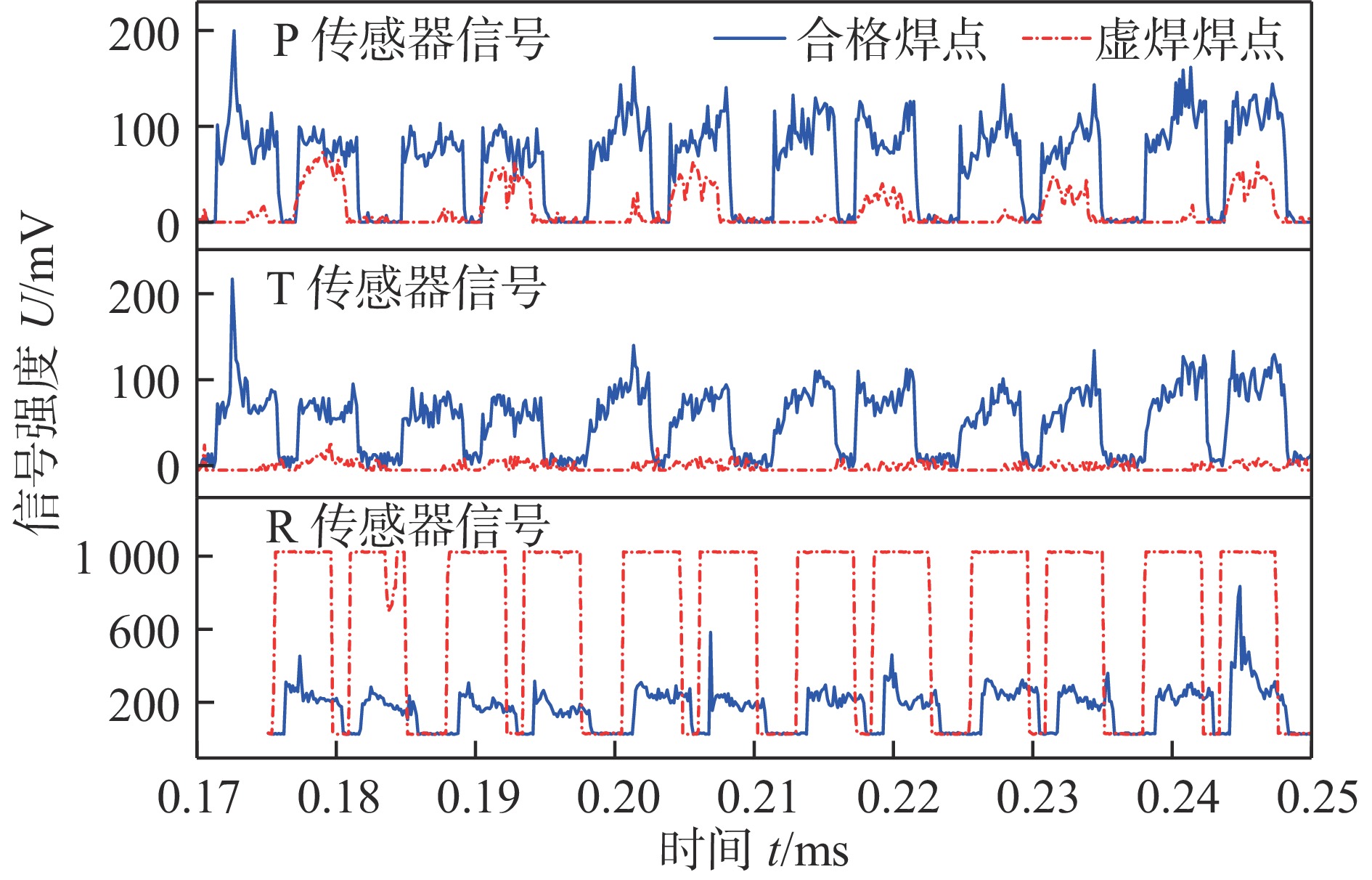
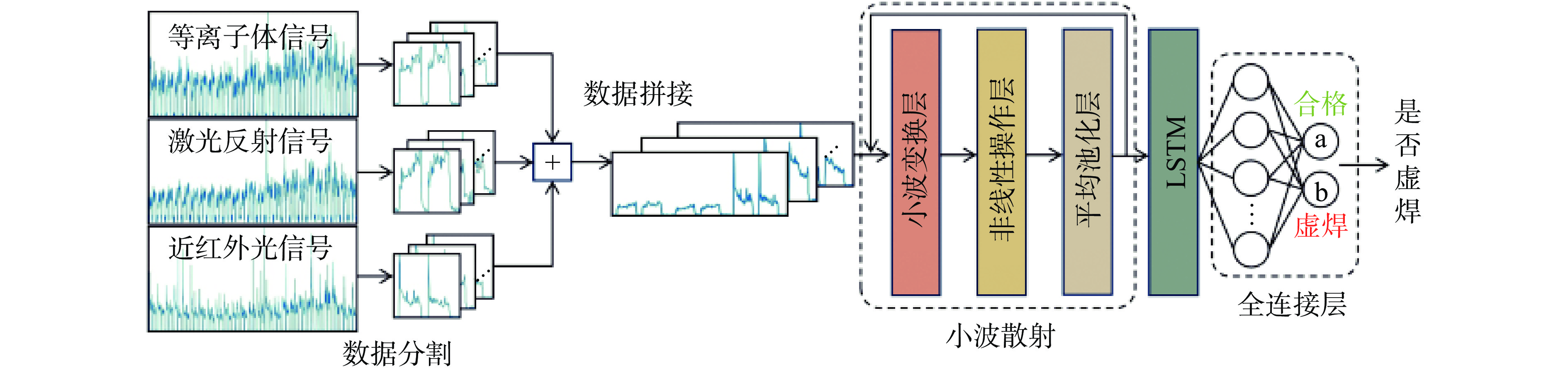
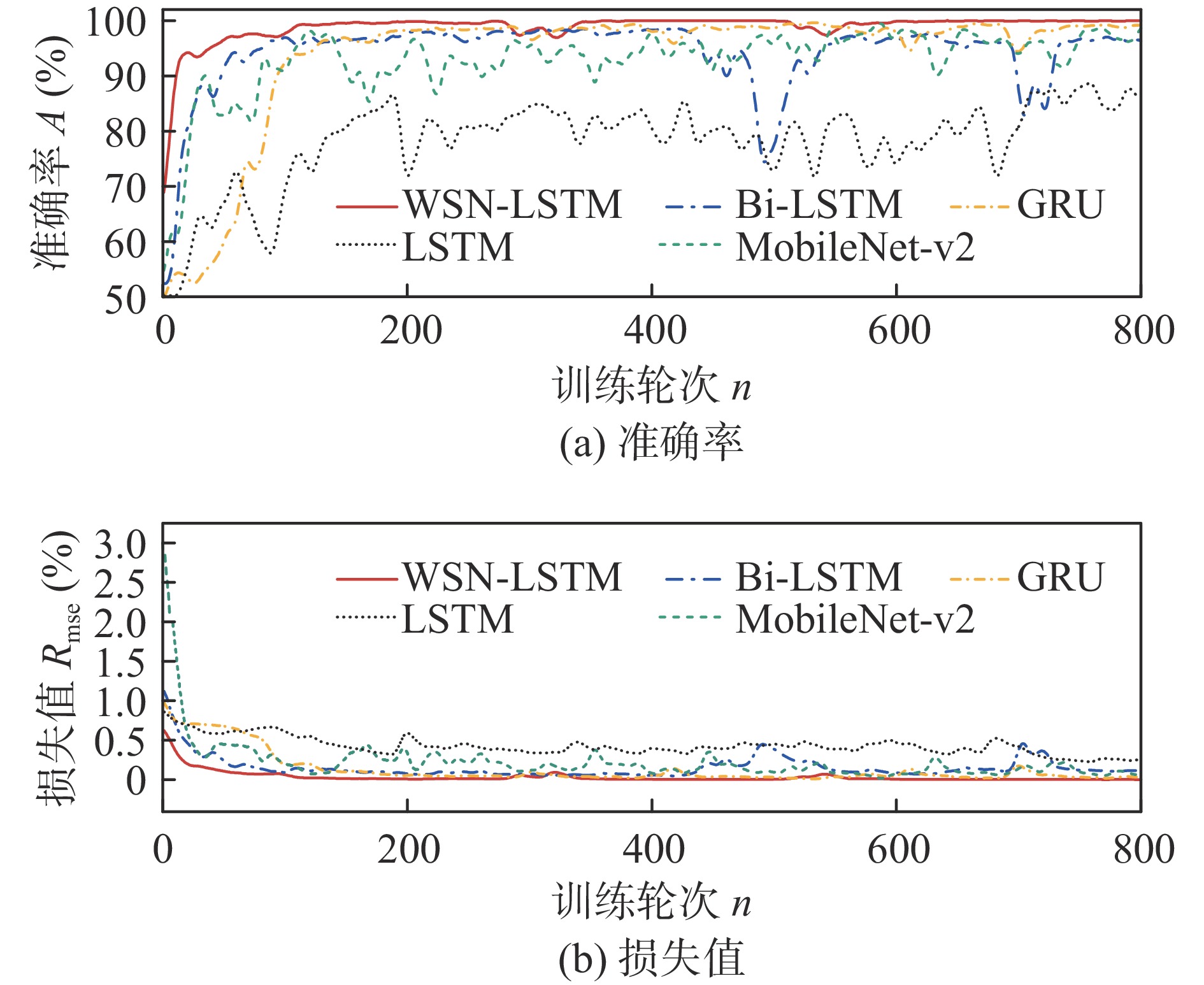
针对多层铝箔极耳和铝片的搭接形式，首先搭建了基于多波段光电同轴传感的激光焊过程实时监测系统，开展了不同激光功率和离焦量的激光焊试验，实时采集不同激光能量下的多波段光电信号；其次，利用小波散射网络从原始信号中提取出多尺度高维特征，并结合长短期记忆网络实现时间动态建模，最终达到实时检测虚焊缺陷的目标. 结果表明，在小样本规模下，构建的WSN-LSTM模型准确率达到99.6%，其分类性能优于其他循环神经网络和轻量化卷积神经网络模型. 同时，WSN-LSTM模型轻量化使其在训练时间最短，且平均单个样本处理时间仅为0.15 ms，有利于在动力电池产线快速部署，并实现虚焊缺陷的实时检测.
Abstract:Targeting the lap joint of multilayer aluminum tabs and an aluminum sheet, a real-time monitoring system for the laser welding process based on multi-band photoelectric coaxial sensing was established. Experiments on laser welding processes with different laser powers and defocusing conditions were conducted, and multi-band photoelectric signals under different laser energies were collected in real-time. Secondly, a wavelet scattering network (WSN) was used to extract multi-scale high-dimensional features from the raw signals. Combined with a long short-term memory (LSTM) network for temporal dynamic modeling, this approach ultimately achieves the goal of real-time detection of pseudo welding defects. The results indicate that, with a small sample size, the constructed WSN-LSTM model achieves an accuracy of 99.6%, and its classification performance surpasses that of other recurrent neural networks and lightweight convolutional neural network models. Additionally, the lightweight characteristic of the WSN-LSTM model results in the shortest training time, with an average processing time per sample of only 0.15 ms, making it advantageous for rapid deployment on power battery production lines and real-time detection of pseudo welding defects.
-
0. 序言
太空金属增材制造技术已应用于轨道金属零件的制造和维修，它将成为未来航空制造领域的重要研究方向[1-3]. 目前金属增材制造技术所采用的热源是以激光束、电子束、等离子束和电弧束为主[4-5]. 与地面环境不同，空间环境对金属增材制造技术提出了严峻的挑战，包括当前的传热系统，增材制造工艺和热源设备等[6-7]. 使用激光束作为热源的金属丝材增材制造技术具有高能量密度、高精度、高效率和高柔韧性的优势[8-9]，但是这种方法装置结构比较复杂，功率输出高，能量利用率较低. 与激光热源相比，电子束热源具有更高的能量利用率，因此这种方法的设备结构也相对复杂[10-11]. 以等离子束为热源的丝材增材制造技术具有输入热量高、利用率高、制造效率高、制造速度快的特点[12-13]，然而由于空间中低压环境的影响，电弧难以起弧，以上热源方法都适用于空间环境制造. 课题小组提出了一种适用于太空环境的金属制造方法，电阻加热金属丝的增材制造技术[14]，电流通过金属丝材转换为焦耳热，金属熔化涂覆成形. 这种方法的优点是热效率高，热量输入控制精确，设备简单[15-17]，但是金属丝材熔化形成熔体之后容易产生变形[14]，这对金属丝材成形过程造成极大的不稳定因素.
Wei等人[18]观察电流密度为1.25和4.0 mA/cm2时，Cu低电介质互连结构的形成和生长. Budiman等人揭示了电迁移引起的铜互连线塑性变形对失效时间的可能影响. Zhang等人[19]在573和623 K下观察了铜导线电迁移过程中的局部熔化，大部分工作集中在铜互连中电迁移产生的缺陷和损伤上. Park和Zhang等人[19-20]使用交流电流研究了铜互连的热疲劳.然而对于铜线和铜互连线中的局部熔合和电流诱导变形的研究很少. 材料在电流作用下的行为取决于局部的电-热-机械相互作用.
当短路电流通过金属丝材时，金属丝材经历了电-热-机械的变形，为了精确探究金属熔体的塑性变形，文中研究了短路电流通过金属丝材时，金属丝材的电熔合电流诱导变形，讨论了金属丝材变形与电流密度的关系，数值分析金属熔体的塑性机-电-热响应.
1. 试验系统与方案
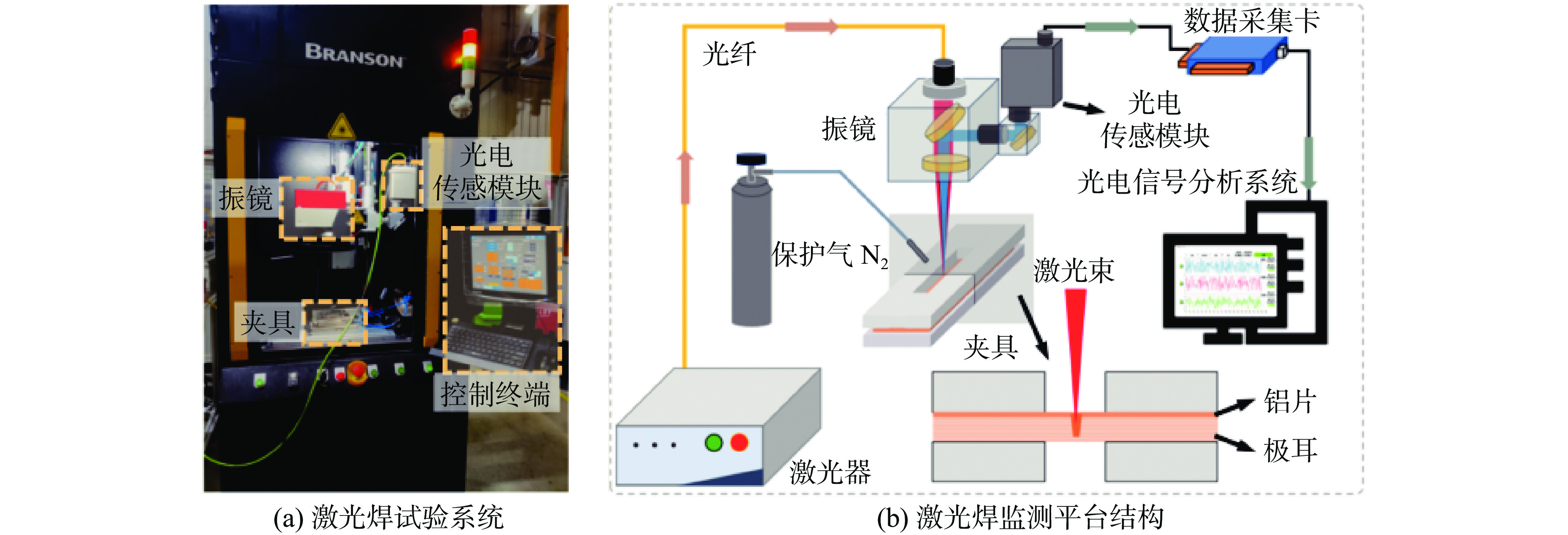
为了研究电阻加热金属丝材熔化过程的塑形变形，避免基板散热不均匀对金属丝熔化过程的影响，设计了等直径导电喷嘴夹持金属丝熔化的物理试验系统，如图1所示. 金属丝材通过两个同轴的导电嘴，可编程电源输出电流，短路电流流过金属丝材本体产生焦耳热，热量累积，金属丝材熔化. 采用热像仪Optris Pi-Xi 400采集金属丝材熔化过程的温度变化，采用美国 IDT 公司的 Motion Pro-Y4 高速摄像机采集金属丝材的变形，由电压传感器CHV-25P、电流传感器CHB-500S采集金属丝材熔化过程电信号的变化. 上位机通过NI采集卡同步采集金属丝材熔化过程的电信号和温度变化.
采用最普遍的金属材料Q235钢，金属丝材通过先进的电镀铜工艺制作，具有较强的脱氧性，可以降低熔化过程的含氧量，保证焦耳加热金属丝材熔化的成形质量. 试验前使用超声波清洁机用丙酮清洁所有样品，将金属丝材在773 K的空气中进行1 h的热处理，以释放加工和拉拔产生的残余应力，并将金属丝材安装至同轴的两个电极之间.
不同的电流密度会导致金属丝材存在不同的塑性变形，在电阻加热金属丝材熔化过程，影响电流密度的主要参数为电流值和丝材直径. 因此为了研究不同电流密度对金属丝材变形的影响. 设计了7套方案，具体试验参数如表1所示.
表 1 电阻加热金属丝材试验方案Table 1. Experimental scheme of resistance heating wire试验方案 电流值I/A 电流波形 电极距离d/mm 丝材直径w/mm 1-1 60 恒流电流 6.0 1.2 1-2 80 恒流电流 6.0 1.2 1-3 100 恒流电流 6.0 1.2 1-4 120 恒流电流 6.0 1.2 2-1 80 恒流电流 6.0 0.8 2-2 80 恒流电流 6.0 1.2 2-3 80 恒流电流 6.0 1.6 2. 试验结果
电流通过金属丝材并释放焦耳热，Zhao等人[21]分析了电流通过导电体的稳态温度分布. 假设材料的性质与温度无关，金属丝材的温度分布为
$${{T}} = \int_0^L {\left[ {\left( {{T_0} - {T_\infty } - \frac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right)\dfrac{{{\rm{cosh}}\omega x}}{{\cosh \left( {\dfrac{{\omega L}}{2}} \right)}} + {T_\infty } + \dfrac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right]{\rm{d}}L} $$ (1) 式中：T0为金属丝材端部温度；T∞为环境温度(即离表面适当远的温度)；A为金属丝材横截面积；J为电流密度；c为单位长度表面积之和；ρe为电阻率；hc为传热系数；L为金属丝材的长度；ω2=chc/kA；其中ω为总传热热阻，k为热导系数.
图2为80 A恒流电流通过长度4 mm，直径1.2 mm的金属丝材熔化过程图像. 由图像可示，在加热初期，金属丝材中部的温度较高. 加热中期，热量累积，金属丝材中间的温度逐渐升高，高温区域逐渐增大，金属丝材的热量由中部沿金属丝材轴向电极两端方向呈带状传导，金属丝材的温度逐渐升高. 加热末期，金属丝材中间高温区域增大，熔化的金属丝材柔性变形，在温度最高区域形成缩颈.
在短路电流通过金属丝材的过程中，电流强度保持恒定，通过高速摄像记录金属丝材塑性变形程度. 在恒流电流为80 A的作用下，丝材直径分别为0.8，1.2和1.6 mm，长度为6 mm的金属丝材的挠度变化见图3，通过三种金属丝材的电流密度分别为15.924，7.077，3.981 kA/cm2. 在短路电流流过金属丝材之后，随着时间的变化，金属丝材开始熔化和偏转，金属丝材中心部分向下移动，最大挠度随时间增加而增大. 这种行为类似于在承受轴向压缩载荷时弹性梁的屈曲. 值得注意的是，高温区域始于金属丝材的中心位置，并随着时间的增加而逐渐向金属丝材的两端延伸. 最后，在金属丝材的中部出现局部熔化并伴有强烈的热辐射. 在短路电流作用下，热量累积，电熔之后，金属丝材的几何构型与发生电熔之前的几何构型保持大致相同. 结果表明，由于电流的通过，金属丝材经历了塑性变形. 也观察到向上的偏转，偏转方向取决于初始状态下的局部表面曲率.
![]()
图 3 电阻加热金属丝材熔化过程随时间变化的挠度Figure 3. Time-dependent deflection of resistance heated wire during melting. (a) w = 0.8 mm; (b) w = 1.2 mm; (c) w = 1.6 mm3. 讨论与分析
电阻加热金属丝材熔化后容易发生变形，金属熔体过渡过程在一定范围内的变形可以控制金属熔体的形貌，但是过大的变形容易导致熔体过渡不稳定和熔体形状的不可控. 因此金属丝材熔化过程的金属熔体的电热力学行为控制对机电结构完整性具有重要作用. 短路电流密度通过金属熔体后易引起了机-电-热的相互作用，导致金属丝材的热影响区、半熔化区和熔化区的晶粒长大、旋转变化，使得熔化后的金属丝材的产生弹塑性屈曲变形.
图4为电阻加热金属丝材最大挠度随时间变化趋势，随着电流密度的增加，金属丝材的挠度增大，总应变与电流密度的关系为二次函数变化. 金属丝材在短路电流加载之前(即未熔化之前)存在一个准稳态. 短路电流加载后，其电阻和温度将随时间增加而有各自的变化规律. 众所周知，由于高电流密度的电流通过金属丝材时，金属丝材在焦耳热的作用下熔化，金属丝材形成熔体后经历电-热-机械变形，从而导致金属丝材的机械强度大大减弱，从而导致金属丝材的结构失效. 电阻加热金属丝材熔化在电流作用下的行为，取决于金属丝材局部的电-热-机械的相互作用.
![]()
图 4 电阻加热金属丝材最大挠度随时间变化趋势Figure 4. Variation trend of maximum deflection of resistance heating wire with time根据电流通过金属丝材释放的焦耳热，得到了电流流过长度L的金属丝材的温度分布如式(1)所示. 假设金属丝材的材料性质与温度无关，对于较小电流密度电流通过金属丝材时，金属丝材会产生小变形，金属丝材的挠度可以用线弹性来描述. 通过两个同轴导电嘴的金属丝材的平均电-热应变见式(2).
$${\varepsilon _{\rm{therm}}} = - \frac{\alpha }{L}\int \limits_{ - L/2}^{L/2} {\left( {T - {T_\infty }} \right){\rm{d}}x} $$ (2) 式中：εtherm为金属丝材的平均电-热应变，将式(1)代入式(2)，可得
$$\begin{split} {\varepsilon _{\rm{therm}}} = - \alpha \left[ {\left( {{T_0} - {T_\infty } - \frac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right)\frac{{{\rm{tanh}}\left( {\omega L/2} \right)}}{{\omega L/2}} + \frac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right]\\ \end{split}$$ (3) 电流诱发的金属丝材的轴向力见式(4).
$$\begin{split} F \!=\! \sigma A \!= \!- \alpha EA\left[ {\left( {{T_0} \!-\! {T_\infty } \!-\! \frac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right)\frac{{{\rm{tanh}}\left( {\omega L/2} \right)}}{{\omega L/2}} \!+\! \frac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right]\\ \end{split}$$ (4) 式中：F为轴向力；σ为金属丝材的应力；α为膨胀系数，E为杨氏模量.
金属丝材在压缩轴向力的作用下，弹性梁曲度(侧向挠度)的存在是一个临界载荷. 金属丝材屈曲的临界载荷取决于金属丝材的尺寸和弹性模量见式(5).
$$ {F_{\rm{cr}}} = - \frac{{{{\text{π}} ^2}E{w^4}}}{{3{L^3}}} $$ (5) 式中：w为金属丝材的直径. 此处金属丝材的宽度和厚度相等，需要注意负号表示对金属丝材的压缩力.
将式(4)带入式(5)中，可得到电阻加热金属丝材的短路电流诱发屈曲的临界电流密度见式(6).
$$\begin{split} {J_{\rm{cr}}} = &{\left( {\frac{{c{h_{\rm{c}}}}}{{{\rho _{\rm{e}}}w^2}}} \right)^{1/2}}{\left( {\frac{{{{\text{π}} ^2}{w^2}}}{{3\alpha {L^2}}} - \left( {{T_0} - {T_\infty }} \right)\frac{{{\rm{tanh}}\left( {{\rm{\omega L}}/2} \right)}}{{\omega L/2}}} \right)^{1/2}} \times {\left( {1 - \frac{{{\rm{tan}}\left( {\omega L/2} \right)}}{{\omega L/2}}} \right)^{ - 1/2}} \end{split}$$ (6) 临界电流密度与金属丝材材料的弹性性质无关，相对于相同长度的弹性金属丝材，临界电流密度随着金属丝材直径的减小而增大，而相对于相同界面尺寸的金属丝材，临界电流随着金属丝材长度的增大而减小. 需要注意，上述分析是基于式(5)的弹性屈曲. 圆柱形金属丝材的塑性曲度的应力计算需要考虑金属丝材塑性变形的应力应变关系，对于具有小挠度的金属丝材塑性屈曲，最大的挠度见式(7).
$$\delta = - \frac{{6Fe{L^2}}}{{{Ew^4}}}$$ (7) 式中：δ为金属丝材的最大挠度，将式(4)带入式(7)，可得
$$\begin{split} \delta = - \frac{{6\alpha e{L^2}}}{{{w^2}}}\left[ {\left( {{T_0} - {T_\infty } - \frac{{{\rho _{\rm{e}}}wt{J^2}}}{{c{h_{\rm{c}}}}}} \right)\frac{{{\rm{tanh}}\left( {\omega L/2} \right)}}{{\omega L/2}} + \frac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right]\\ \end{split}$$ (8) 式中：e为离心率.其最大挠度是短路电流密度的平方的线性增加函数，并且随着金属丝材长度的增加而增加. 金属丝材在短路电流的作用下，导致金属丝材产生机电响应，产生塑性变形.
在准稳态周期中金属丝材的最大挠度随电流密度的变化如图5所示. 准稳态期间的最大挠度与电流密度的增加呈线性关系，与式(8)的平方相关性相反，这种差异是由于金属丝材的塑性变形导致的.当金属丝材通过高电流密度的电流时，电阻热导致金属丝材中的温度升高，如图3所示，屈服应力降低. 屈服应力的减小和温度的升高使得在电流引起的热轴向载荷的作用下，容易在金属丝材中引起塑性变形. 对于相同横截面面积的金属丝材，在相同电流密度的作用下，最大挠度随金属丝材长度的增加而定性地增加，这与理论计算分析相一致. 如图5所示，dδ/(L·dJ)的比率对于这项工作中使用的试验条件大致是一个常数，它这个比率与金属丝材的长度和电流密度无关，控制这种行为的机制尚不清楚.
![]()
图 5 金属丝材在准稳态周期中的最大挠度随电流密度变化Figure 5. Maximum deflection of a metal wire in a quasi-steady-state period varies with current density通常金属丝材的最大挠度的变化与金属丝材长度∆L的变化有关，如图4所示，金属丝材的挠曲轮廓近似为
$$f = \frac{\delta }{2}\left( {1 + {\rm{cos}}\frac{{2{\text{π}} r}}{L}} \right)$$ (9) 式中：f为金属丝材的挠度；r为金属丝材的半径.
式(9)已被广泛用于分析弹性梁的屈曲. 然而如图3所示的金属丝材也经历了弹塑性变形，这表明等式在σ/L<0.09的条件下，式(9)也可以用来近似估计金属丝材的弹塑性屈曲. 因此金属丝材的长度变化见式(10).
$$\Delta L = \mathop \int \limits_{ - L/2}^{L/2} \sqrt {1 + {{\left( {\frac{{{\rm{d}}w}}{{{\rm{d}}x}}} \right)}^2}} {\rm{d}}x - L \approx \frac{{{{\text{π}} ^2}{\delta ^2}}}{{4L}}$$ (10) 在σ/L<0.09的情况下，在准稳态周期内，总应变可以近似为∆L/L，即
$${\varepsilon _{\rm{T}}} \approx \frac{{\Delta L}}{L} \approx \frac{{{{\text{π}} ^2}}}{4}\frac{{{\delta ^2}}}{{{L^2}}}$$ (11) 式中：εT为金属丝材的总应变，根据图5的结果见式(12).
$$\frac{{{L^{ - 1}}{\rm{d}}\delta }}{{{\rm{d}}J}} = \chi $$ (12) 式中: χ取决于金属丝材的材料属性和几何构型. 将式(12)代入式(11)可得
$${\varepsilon _{\rm{T}}} \approx \frac{{{{\text{π}} ^2}}}{4}{\left( {\chi J + {\zeta _{_{\rm{C}}}}} \right)^2}$$ (13) 式中：ζc为金属丝材最大挠度的轴柱上的截距.
对于金属丝材通过电流密度高的电流引起的屈曲变形，根据所使用的试验条件，得出总应变是电流密度的二次函数.
金属丝材的总应变由弹性应变εe，热应变εtherm和塑性应变εp组成，即
$${\varepsilon _{\rm{T}}} = {\varepsilon _{\rm{e}}} + {\varepsilon _{\rm{t}}} + {\varepsilon _{\rm{p}}}$$ (14) $${\varepsilon _{\rm{e}}} = \frac{1}{L}\mathop \int \limits_{ - L/2}^{L/2} \frac{{\sigma {\rm{d}}x}}{E} + \frac{{\zeta {J^2}w^2}}{{2L}}\mathop \int \limits_{ - L/2}^{L/2} \frac{{v{\mu _{\rm{m}}}{\rm{d}}x}}{E}$$ (15) $${\varepsilon _{\rm{therm}}} = - \frac{1}{L}\mathop \int \limits_{ - L/2}^{L/2} \alpha \left( {T - {T_\infty }} \right){\rm{d}}x$$ (16) 式中：ζ为金属丝材的几何因子；v为泊松比；μm为磁导率. 对于应变硬化材料，塑性应变和应力之间的关系见式(17).
$${\varepsilon _{\rm{p}}} = a{\sigma ^n}$$ (17) 式中：a为预因子；n为应力指数.
将式(13)，式(15)，式(16)和式(17)分别代入式(14)，可以得到金属丝材中的电流感应应力与电流密度的关系
$$\begin{split} \frac{1}{L}\mathop \int \limits_{ - L/2}^{L/2} \frac{{\sigma {\rm{d}}x}}{E} + \frac{{\zeta {J^2}w^2}}{{2L}}\mathop \int \limits_{ - L/2}^{L/2} \frac{{v{\mu _{\rm{m}}}{\rm{d}}x}}{E} - \frac{1}{L}\mathop \int \limits_{ - L/2}^{L/2} \alpha \left( {T - {T_\infty }} \right){\rm{d}}x +\frac{1}{L}\mathop \int \limits_{ - L/2}^{L/2} a{\sigma ^2}{\rm{d}}x = \frac{{{{\text{π}} ^2}}}{4}{\left( {\chi J + {\zeta _{\rm{c}}}} \right)^2}\\[-12pt] \end{split}$$ (18) 如果金属丝材的材料特性中温度依赖性可以忽略不计，则式(18)可简化，见式(19).
$$ \begin{split} \dfrac{\sigma }{E} \!+\! \dfrac{{\zeta v{\mu _{\rm{m}}}{J^2}w^2}}{{2EL}} \!-\! \alpha \left[ {\left( {{T_0} \!-\! {T_\infty } \!-\! \dfrac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right)\dfrac{{\tanh \left( {\dfrac{{\omega L}}{2}} \right)}}{{\dfrac{{\omega L}}{2}}}\! +\! \dfrac{{{\rho _{\rm{e}}}A{J^2}}}{{c{h_{\rm{c}}}}}} \right] \!+ a{\sigma ^n} = \dfrac{{{{\text{π}} ^2}}}{4}{\left( {\chi J + {\zeta _{\rm{c}}}} \right)^2}\\[-12pt] \end{split} $$ (19) 从以上可以得到，应力演变是电流密度的二次函数，从电压值随时间的变化趋势，可以确定当承受高电流密度的电流时，金属丝材的断裂时间(电熔断). 如预期的那样，金属熔体的断裂时间随电流密度的增加而减少，这是因为局部温度随电流密度的增加而增加，如式(8)所示. 相对低电流密度的电流指数随金属丝材的增加而减小，而对于较高电流密度，它相对独立于金属丝材的几何尺寸. 金属丝材的表面氧化对电熔存在一定影响，随着氧化层的生长，用于电流通过的截面积减小，局部温度升高，这种趋势加速了金属丝材的熔断. 对于小电流指数的区域，随着高电流密度的电流的通过，焦耳热的快速释放限制了表面氧化层的生长，电流引起的熔断是主要的. 对于大电流指数区域，这是表面氧化和焦耳的耦合. 影响金属丝材塑性应变的变量主要有电流大小、金属丝材直径、金属丝材长度. 由理论计算结果与试验数据的比较，数值计算结果与试验数据吻合良好. 数值计算结果与最大挠度的试验结果之间的差异很可能是由于表面氧化物的作用，使金属丝材变硬并限制了电流引起的金属丝材的挠度，同样存在收缩效应，这增加了金属丝材的刚度. 数值计算既不考虑表面氧化物的贡献，也不考虑收缩响应分析的复杂性.
4. 结论
(1)数值计算得出最大挠度是电流密度的线性函数，与试验结果一致.
(2)金属丝材熔化后，通过电流高密度的金属丝材会发生显着的塑性变形，会造成极大的不稳定性.
(3)在高电流密度电流的作用下，释放出大量的焦耳热会引起局部温度的显着升高，从而导致屈服应力的降低，并且由于电-热-机械相互作用的原因，容易在金属熔体引起塑性变形.
-
![]()
图 1 试验平台结构
Figure 1. Experimental platform structure. (a) laser welding workstation; (b) welding and monitoring platform structure
![]()
图 3 焊缝形貌和金相横截面
Figure 3. Qualified and pseudo weld seam morphology, metallographic cross-section. (a) qualified weld seam; (b) qualified metallographic cross-section; (c) pseudo weld seam; (d) pseudo metallographic cross-section
![]()
图 5 轻量化虚焊缺陷检测模型总体框架
Figure 5. Overall framework of the lightweight pseudo welding defect detection model
![]()
图 6 不同模型在训练集上准确率与损失值的迭代曲线
Figure 6. Iteration curves of accuracy and loss values on the training set for different models. (a) accuracy; (b) loss values
表 1 焊接工艺参数
Table 1 Welding experiment paraments
激光功率P/W 离焦量Df /mm 320，360，400，440，480 −2，−1，0，1，2 
下载: 导出CSV
表 2 不同模型的性能对比
Table 2 2 Performance comparison of different models
模型
类别准确率
A(%)精确率
P(%)召回率
R(%)F1分数
F1(%)模型参量
N/KB训练时间
t1/s样本平均时间
t2/msWSN-LSTM 99.6 99.6 100 99.8 55.8 26 0.15 LSTM 89.2 84.8 99.3 91.4 160.6 49 0.52 Bi-LSTM 97.4 98.9 96.3 97.6 321.2 82 0.85 GRU 97.2 96.8 97.6 97.2 120.5 61 0.35 MobileNet-v2 96.8 94.8 99.2 97.0 3 589.2 518 4.37
下载: 导出CSV
-
[1] 张杰. 碳/铝复合集流体的制备及其锂电池应用[D]. 南京: 南京邮电大学, 2024. Zhang Jie. Preparation of carbon/aluminum composite collector and their application in lithium battery[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2024.
[2] 王臣, 袁美蓉, 马茵婷, 等. 集流体在锂电池中的研究进展和应用[J]. 化工管理, 2023, 36: 151 − 155. Wang Chen, Yuan Meirong, Ma Yinting, et al. Research progress and application of current collectors in lithium-ion batteries[J]. Chemical Engineering Management, 2023, 36: 151 − 155.
[3] Das A, Li D Z, Williams D, et al. Joining technologies for automotive battery systems manufacturing[J]. World Electric Vehicle Journal, 2018, 9(2): 22. doi: 10.3390/wevj9020022
[4] 杨彪, 刘福运, 檀财旺, 等. 动力电池激光焊接技术的应用现状与展望[J]. 机械制造文摘(焊接分册), 2023(2): 1 − 9. Yang Biao, Liu Fuyun, Tan Caiwang, et al. Current application status and prospects of laser welding technology for power battery[J]. Welding Digest of Machinery Manufacturing, 2023(2): 1 − 9.
[5] 徐东辉, 孟范鹏, 孙鹏, 等. 基于深度学习的GMAW焊接缺陷在线监测[J]. 焊接学报, 2024, 45(3): 114 − 119. Xu Donghui, Meng Fanpeng, Sun Peng, et al. On-line monitoring of GMAW welding defect based on deep learning[J]. Transactions of the China Welding Institution, 2024, 45(3): 114 − 119.
[6] 白子键, 李治文, 张志芬, 等. 基于电弧光谱的核电堵管TIG焊接质量在线监测[J]. 焊接学报, 2024, 45(5): 8 − 19. Bai Zijian, Li Zhiwen, Zhang Zhifen, et al. On-line monitoring of TIG welding quality of nuclear power plug tube based on arc spectrum[J]. Transactions of the China Welding Institution, 2024, 45(5): 8 − 19.
[7] Zhang Y, Gao X, You D, et al. Online judgment of laser welding process based on time-frequency analyses of in-situ high-speed optical signals[J]. Optik, 2022, 265: 169552. doi: 10.1016/j.ijleo.2022.169552
[8] Wu D, Zhang P, Yu Z, et al. Progress and perspectives of in-situ optical monitoring in laser beam welding: Sensing, characterization and modeling[J]. Journal of Manufacturing Processes, 2022, 75: 767 − 791. doi: 10.1016/j.jmapro.2022.01.044
[9] Wang B, Hu S J, Sun L, et al. Intelligent welding system technologies: State-of-the-art review and perspectives[J]. Journal of Manufacturing Systems, 2020, 56: 373 − 391. doi: 10.1016/j.jmsy.2020.06.020
[10] Li X, Shi Y, Jian Y, et al. Research on welding penetration status monitoring based on Residual-Group convolution model[J]. Optics & Laser Technology, 2023, 163: 109322.
[11] Liu L, Wu J, Li D, et al. Fractional wavelet scattering network and applications[J]. IEEE Transactions on Biomedical Engineering, 2018, 66(2): 553 − 563.
[12] Yu Y, Si X, Hu C, et al. A review of recurrent neural networks: LSTM cells and network architectures[J]. Neural computation, 2019, 31(7): 1235 − 1270. doi: 10.1162/neco_a_01199
-
期刊类型引用(4)
1. 刘伟，岳祚林，徐超，李素丽. 316L不锈钢焦耳热3D打印过程变形量数值分析. 焊接技术. 2024(04): 1-5 . 
百度学术
2. 刘焜，闫朝阳，陈树君，陈希章. 电弧增材热源及轨迹规划研究进展. 焊接学报. 2024(11): 21-34 . 本站查看
3. 刘伟，张鑫，李素丽，李小龙. 基于焦耳热增材制造过程的温度场分析研究. 焊接技术. 2023(10): 1-4 . 百度学术
4. 张鑫，刘伟，张伟博，李小龙. 金属3D打印焦耳热最大变形量数值分析. 焊接技术. 2023(11): 1-5 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 93
- HTML全文浏览量: 13
- PDF下载量: 40
- 被引次数: 4
