Method of current density distribution measurement for non-axisymmetric arc based on spilt anode
-
摘要:
电弧是弧焊过程中熔池金属熔化的能量来源，分裂阳极法是电弧阳极能量密度直接测量的有效方法之一. 常规分裂阳极法是建立在电弧为柱对称结构的基础上，不适用于非柱对称电弧的阳极电流密度测量. 试验提出在两条相互垂直的路径上依次进行分裂阳极电流数据采集的新方法，引入表征电弧不对称度的特征参量，进行椭圆环分割，以计算电弧阳极电流密度分布，修正分裂阳极法. 通过预设的二维高斯分布的电流密度模型, 检验了修正的分裂阳极法的可行性. 结果表明，采用修正的分裂阳极法可以有效计算出电弧阳极电流密度分布. 利用修正后的分裂阳极法实现了非柱对称侧向压缩等离子弧阳极电流密度的测量，与x方向相比，侧向压缩的等离子弧在y方向压缩明显，呈现典型的非柱对称特性.
Abstract:Arc is the energy source for molten pool metal melting in arc welding process, and the split anode method is one of the effective methods to measure the energy density of the arc on the anode directly. The conventional split anode method is based on axisymmetric structure of the arc, and it is unfit for anode current density measurement of non-axisymmetric arc. A new method is proposed by measuring the current of the split anode on two perpendicular paths separately. A parameter was introduced to describe the degree of the arc asymmetry. Elliptic ring segmentation was carried out to calculate the anode current density distribution of the arc, and the split anode method was modified. The modified split anode method was verified by a pre-set two-dimensional Gaussian distribution current density model. The experimental results show that the modified split anode method can effectively calculate the anode current density distribution of the arc. The anode current density distribution of non-axisymmetric side-compressed plasma arc was measured by the modified split anode method. Compared with the x direction, the side-compressed plasma arc is compressed obviously in the y direction, showing a typical non-axisymmetric structure.
-
0. 序言
电弧是弧焊过程中金属熔化的能量输入源，是弧焊研究中重点关注的对象之一. 弧焊过程焊接参数的调节本质上是改变电弧能量、力的大小及分布，从而对母材的熔化、流动及凝固行为产生影响[1-2]. 电弧能量输入是电弧行为研究的关键点[3-4]，由于电弧温度较高，电弧温度和能量分布的测量存在困难.
电弧对工件能量的传输过程主要在电弧与熔池的界面进行，正极性焊接时界面为阳极表面，阳极表面电流密度分布是能有效评定电弧对熔池能量输入大小及分布的特征参量[5]. 分裂阳极法是较为常用的测量电弧阳极表面电流密度分布的方法[6-7]，常规分裂阳极法通过测量分裂的两块阳极中单块阳极的电流变化曲线，推导计算阳极表面电流密度分布.
Nestor[6]采用常规分裂阳极法测量了惰性气体电弧阳极电流密度，忽略了电弧拖尾带来的非对称性；张勤练等人[8]通过常规分裂阳极法测量了柔性等离子弧阳极电流密度；李钊等人[9]通过常规分裂阳极法测量了带旁孔的等离子弧阳极电流密度，均忽略了旁孔带来的电弧非柱对称性对分裂阳极法阳极电流密度测量结果的影响. 常规分裂阳极测量计算阳极表面电流密度是建立在电弧为柱对称、阳极电流密度分布为轴对称的假设基础上，假设距离电弧轴线距离相等处，阳极电流密度相同[6-11].
电弧为柱对称的假设限制了常规分裂阳极法的应用范围，使其对非柱对称电弧的阳极表面电流密度分布的测量存在较大误差. 考虑电弧不对称带来的影响，通过两次路径垂直的分裂阳极铜块电流变化曲线的采集，引入表征电弧不对称程度的特征参量，对分裂阳极法进行修正，拓展分裂阳极对非柱对称电弧阳极表面电流密度分布测量的适用性，降低测量误差.
1. 试验方法
1.1 常规分裂阳极法测量设备及过程
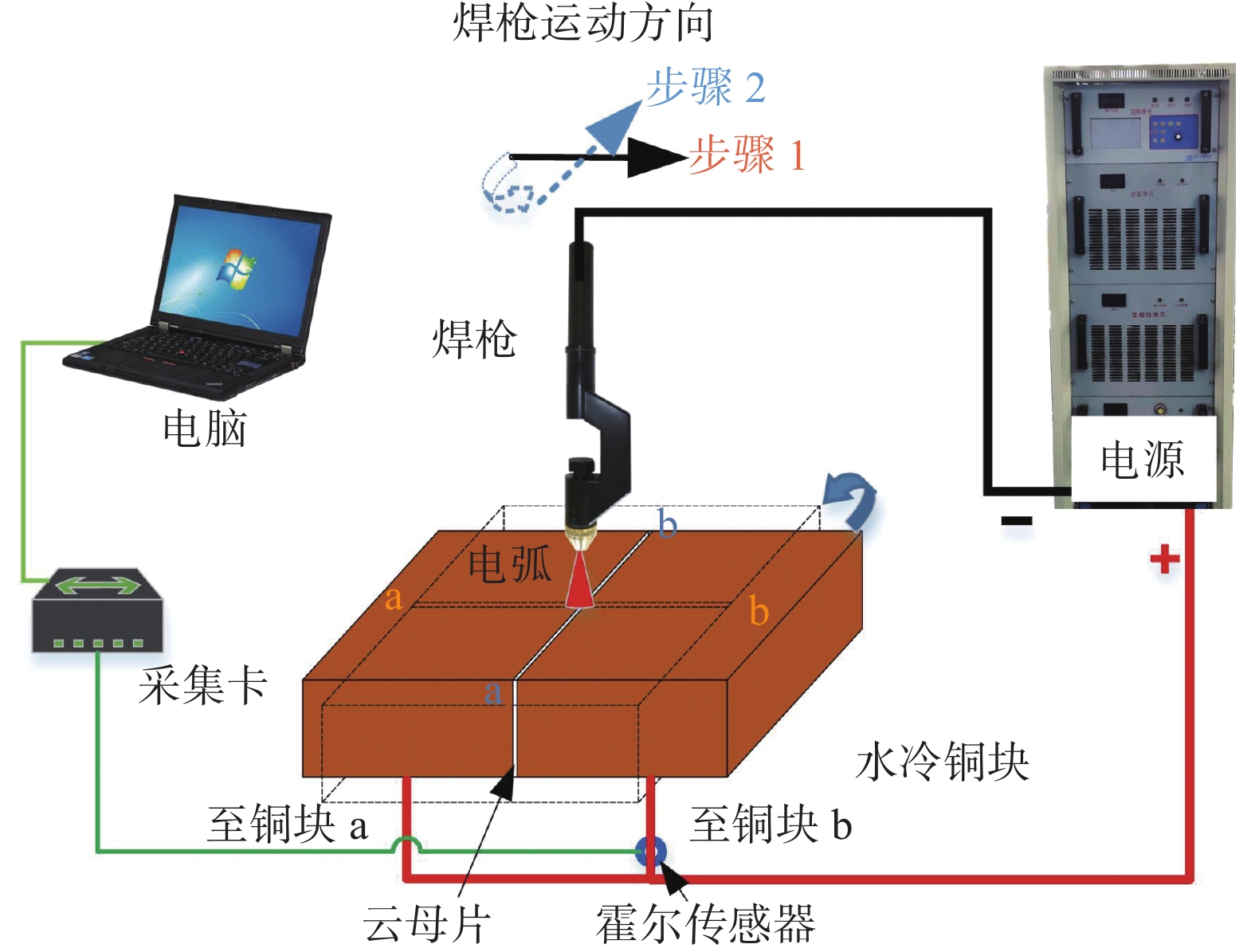
常规分裂阳极法测量设备如图1所示，系统由两块薄云母片隔离绝缘的水冷铜块a和b、霍尔传感器、数据采集卡和上位机组成的测量子系统，以及由焊接电源、焊枪、行走机构组成的焊接子系统组成. 霍尔传感器型号为LHB300A5VY4，电流测量范围为0 ~ ±300 A，数据采集卡型号为阿尔泰USB3200，试验过程采样速率为20 kHz.
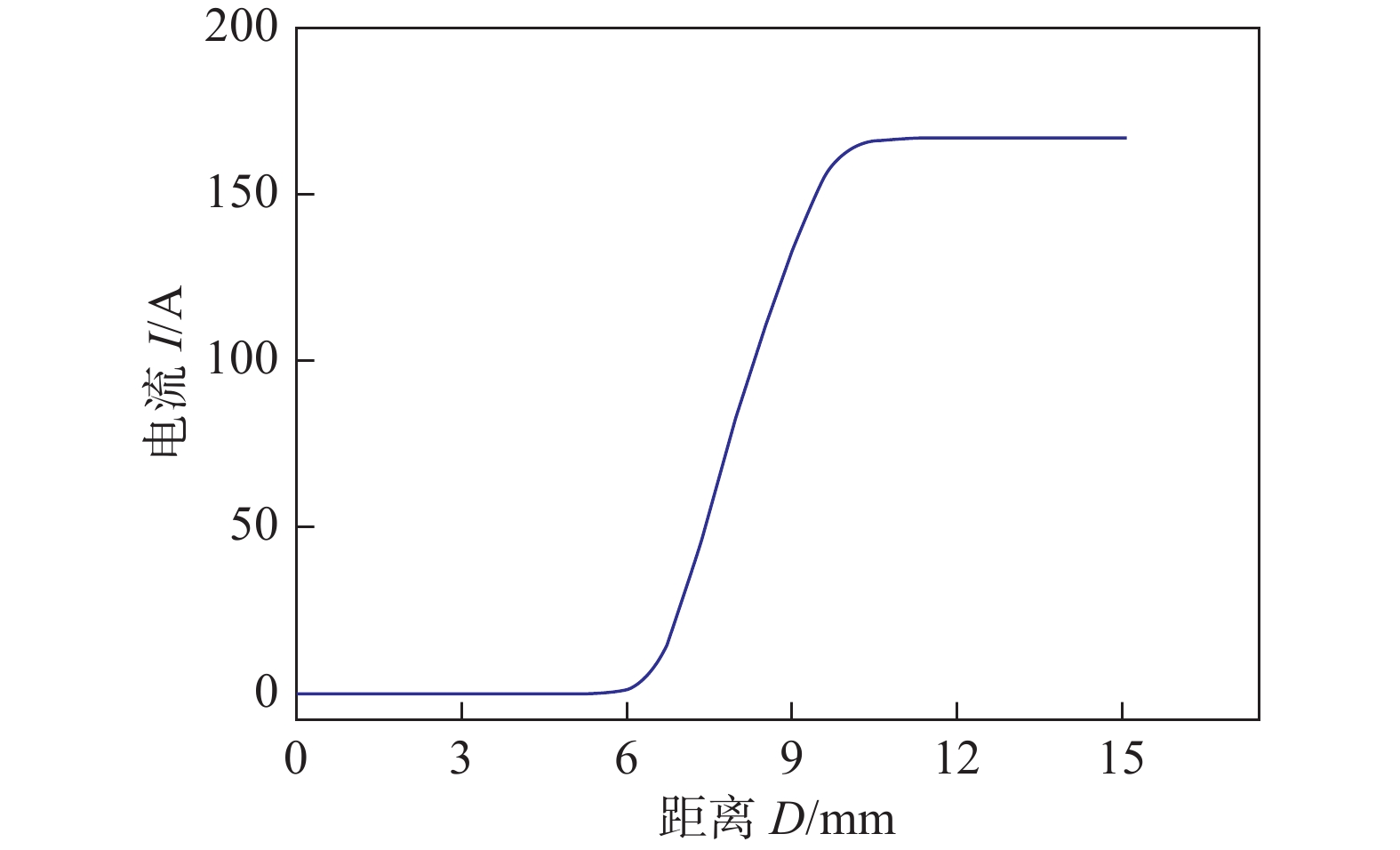
常规分裂阳极法测量过程中，电弧在水冷铜块a上起弧后，由水冷铜块a匀速行走至水冷铜块b，在此过程中测量流经铜块b上的电流时序变化曲线.以焊接电流160 A的电弧为例，测量得到流经铜块b的电流与电弧运动距离关系如图2所示. 常规分裂阳极法建立在电流密度为轴对称分布假设的基础上，通常采用圆环分割的数值计算方法，利用铜块b电流变化计算电弧阳极电流密度变化.
1.2 常规分裂阳极法电流密度计算
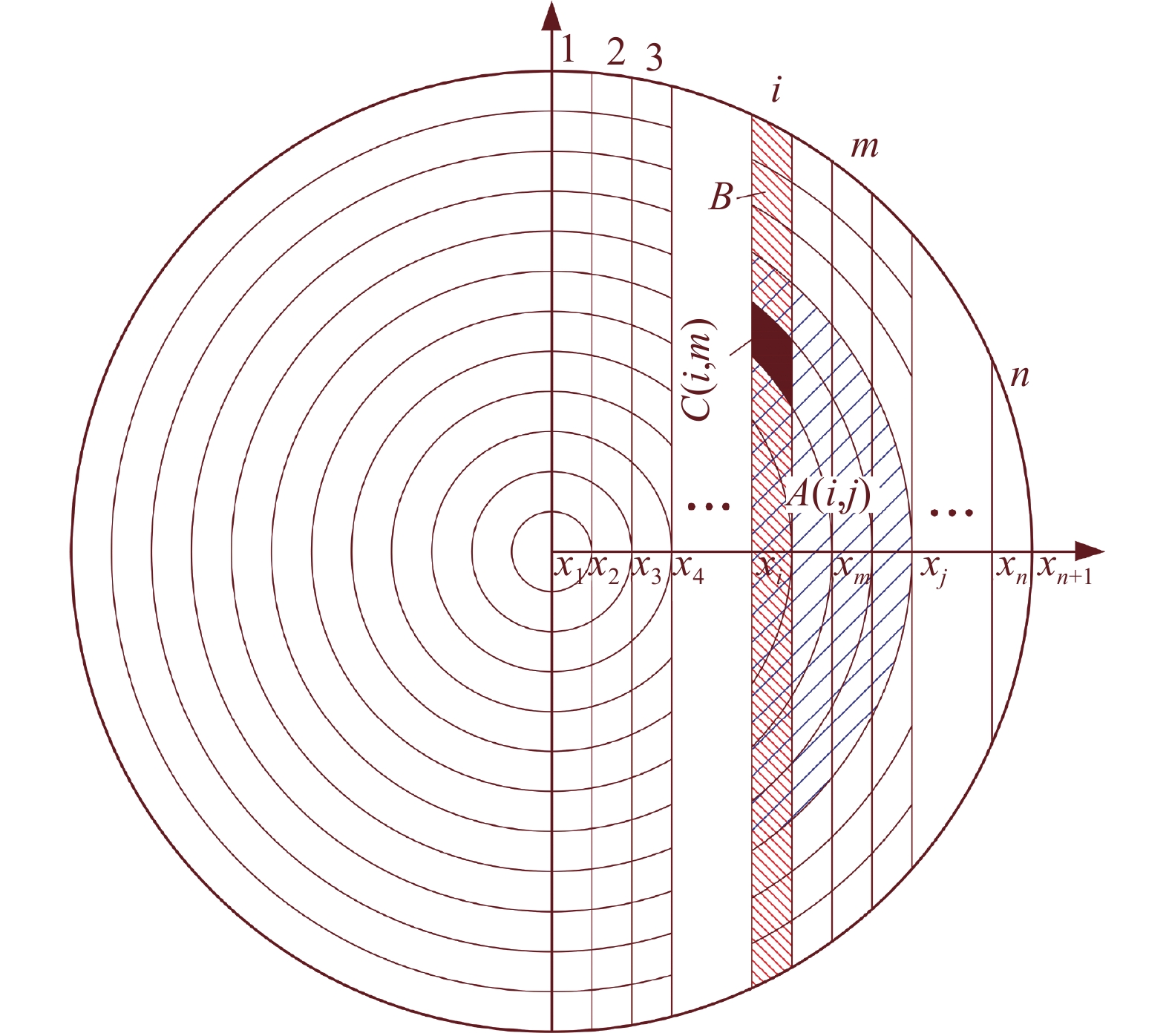
常规分裂阳极法测量计算阳极电流密度分布时，常采用圆环分割法进行数值化处理. 以电弧轴心为原点，在阳极建立相对电弧中心静止的平面运动坐标系. 如图3所示，将电弧按照等间距划分为n个圆环，为保证求解精度，n取值大于100. 在x轴上，原点及圆环与x正半轴的交点共n + 1个坐标，定义为
${x_i}$ ， i为1 ~ (n + 1)的正整数. 电弧由铜块a移动到铜块b过程中，以电弧中心为原点的坐标轴上${x_{n + 1}}$ ，${x_n}$ 和${x_{n - 1}}$ 等坐标点依次移动到铜块b上.![]()
图 3 常规分裂阳极法圆环分割示意图Figure 3. Schematic diagram of ring division for conventional split anode method定义弦
$x = {x_i}$ 及半径为${x_j}$ 的圆围成的弓形区域面积为$A\left( {i,j} \right)$ ，由弦$x = {x_i}$ 和$x = {x_{i + 1}}$ 围成的条状区域为区域B内电流${I_{\rm{B}}}\left( i \right)$ ，由弦$x = {x_i}$ 和$x = {x_{i + 1}}$ 、半径为${x_m}$ 的圆及半径为${x_{m + 1}}$ 的圆所围成的单元面积为$C\left( {i,m} \right)$ ，其中i，j，m均为正整数，且$1 \leqslant i \leqslant m \leqslant j \leqslant n + 1$ .弓形区域面积
$A\left( {i,j} \right)$ 及单元面积$C\left( {i,m} \right)$ 计算式为$$ A(i,j) = \arccos \left(\frac{{{x_i}}}{{{x_j}}}\right) \times {({x_j})^2} - {x_i}\sqrt {{{({x_j})}^2} - {{({x_i})}^2}} $$ (1) 式中：
$ {x_i} $ 和$ {x_j} $ 分别为x轴上的坐标点.$$ \begin{split} C\left( {i,m} \right) = &\frac{1}{2} \times ( {A\left( {i,m + 1} \right) - A\left( {i + 1,m + 1} \right)} -\\&{ A\left( {i,m} \right) + A\left( {i + 1,m} \right)} ) \end{split} $$ (2) 区域B处的电流为
${I_{\rm{B}}}\left( i \right)$ ，计算式为$$ {I_{\rm{B}}}\left( i \right) = 2 \times \mathop \sum \limits_{k = i + 1}^{n + 1} \left( {C\left( {i,k} \right) \times f\left( k \right)} \right) $$ (3) 式中：
$f$ 为电流密度分布数列；$f\left( k \right)$ 为第k个圆环(${x_k} \leqslant r < {x_{k + 1}}$ )处电流密度.定义铜块a和铜块b的间隙在
$x = {x_i}$ 处时，流经铜块b上的电流为$F\left( {{x_i}} \right)$ . 条状区域B的电流${I_{\rm{B}}}\left( i \right)$ 为$$ {I_{\rm{B}}}\left( i \right) = F\left( {{x_i}} \right) - F\left( {{x_{i + 1}}} \right) $$ (4) 电弧运动过程中，试验测量得到的铜块b上电流变化趋势如图2所示，
$F\left( {{x_i}} \right)$ 可以通过电流随运动距离的变化曲线进行坐标变换得到.结合式(1) ~ 式(3)，式(3)可以表述为
$$ {{\boldsymbol{I}}_{\rm{B}}} = {{{\boldsymbol{C}}}} \times {\boldsymbol{f}} $$ (5) 式中：
${{\boldsymbol{I}}_{\rm{B}}}$ 是由${{\boldsymbol{I}}_{\rm{B}}}(i)$ 组成的${{n}} \times 1$ 的矩阵；C为${{n}} \times {{n}}$ 的系数矩阵；${\boldsymbol{f}}$ 为电流密度分布数列，即${{n}} \times 1$ 的矩阵.由式(5)可以推导出电流密度分布
$f$ 为$$ {\boldsymbol{f}} = {C^{'}} \times {{\boldsymbol{I}}_{\rm{B}}} $$ (6) 式中：
$ C^{'} $ 为$C$ 的逆矩阵.由式(6)可求解阳极电流密度分布，其计算过程等效于Abel逆变换数值处理方法.
2. 非柱对称电弧分裂阳极修正
2.1 分裂阳极的修正
利用非柱对称分布的旁孔侧向压缩等离子弧时，电弧不再为柱对称结构[12]，常规分裂阳极法测量阳极电流密度的不再适用. 在分裂阳极法的基础上，分步进行x和y两个方向的铜块电流变化曲线的测量，对常规分裂阳极法进行修正，实现非柱对称侧向压缩等离子弧电弧阳极电流密度测量，测量系统如图4所示，其中定义x方向为电弧宽度最大的方向，y方向与x方向垂直.
在x和y方向测量过程中，测量得到铜块b上电流变化曲线如图5所示，定义铜块b电流由焊接电流的5%增长至95%时铜块移动距离为电弧电流分布宽度，其物理意义为流经此统计区间内的电流占全部电弧电流的90%. 定义x方向电弧宽度为
${a_{\rm{I}}}$ ，y方向电弧宽度为${b_{\rm{I}}}$ . 电弧电流侧向压缩比${R_{\rm{I}}}$ 为$$ {R_{\rm{I}}} = \frac{{{b_{\rm{I}}}}}{{{a_{\rm{I}}}}} $$ (7) 与圆环分割类似，采用相同离心率的椭圆对非柱对称的电弧进行分割处理，如图6所示，其中右侧椭圆弓形区域D的面积为
$$ {S _{\rm{D}}} = \frac{{{\text{π}}ab}}{2} - \frac{b}{a}{x_0}\sqrt {{a^2} - {x_0}^2} - ab \times \arcsin \frac{{{x_0}}}{a} $$ (8) 式中：a和b分别是椭圆的长半轴长和短半轴长；
${x_0}$ 是弓形的弦与轴的交点.基于x和y两个方向测量得到的电弧宽度数值，计算得到电流密度侧向压缩比RI，采用类似圆环分割的计算思路，计算非柱对称侧向压缩等离子体阳极电流密度. 利用椭圆弓形区域D的面积
${S_{\rm{D}}}$ 替代传统分裂阳极法弓形区域面积A，可以推导单元面积C. 根据单元面积C和电流密度f，可以表述条状区域B的电流为${I_{\rm{B}}}$ ，见式(5)，同时可以通过铜块b的电流计算${I_{\rm{B}}}$ ，见式(4)，最终可以通过铜块b电流反推电弧阳极电流密度分布，见式(6)，实现阳极电流密度分布的测量计算.2.2 方法有效性的验证
为验证修正的分裂阳极法对非柱对称侧向压缩等离子弧阳极电流密度测量的有效性，预设标准电流密度分布，校验修正后的分裂阳极算法有效性. 将非柱对称侧向压缩的等离子弧电流密度分布抽象为二维高斯分布(two-dimensional Gaussian distribution)，二维高斯分布方程为
$$ \begin{split} & g\left( {x,y} \right) = \frac{1}{{{2{\text{π }}{\sigma _1}{\sigma _2}}}\sqrt{\left(1-\rho^2\right)}} \times {\text{exp}}\\&\left( { - \frac{1}{{2(1 - {\rho ^2})}}\left( {\frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{{\sigma _1}^2}}}+ \right.} {\left. { \frac{{{{\left( {y - {\mu _2}} \right)}^2}}}{{{\sigma _2}^2}}{\kern 1pt} {\kern 1pt} - \frac{{2\rho \left( {x - {\mu _1}} \right)\left( {y - {\mu _2}} \right)}}{{{\sigma _1}{\sigma _2}}}} \right)} \right) \end{split}$$ (9) 式中：
$\rho $ 为相关系数；${\mu _1}$ 和${\mu _2}$ 为期望；${\sigma _1}$ 和${\sigma _2}$ 为x和y方向上的标准差.两次测量沿长轴和短轴方向，
$\rho = 0$ 时，式(9)可以简化为$$ g\left( {x,y} \right) = \frac{1}{{2{\text{π }}{\sigma _1}{\sigma _2}}}{\text{exp}}\left( { - \frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{2{\sigma _1}^2}} - \frac{{{{\left( {y - {\mu _2}} \right)}^2}}}{{2{\sigma _2}^2}}} \right) $$ (10) 借助于二维高斯分布，验证修正后的分裂阳极法测量阳极电流密度的算法的可行性. 假设电流密度满足二维高斯分布，其表达式为
$$ f\left( {x,y} \right) = \frac{{{I}}}{{2{\text{π }}{\sigma _1}{\sigma _2}}}\exp \left( { - \frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{2{\sigma _1}^2}} - \frac{{{{\left( {y - {\mu _2}} \right)}^2}}}{{2{\sigma _2}^2}}} \right) $$ (11) 式中：I为焊接电流.
x方向积分得到的电流时序曲线是
$$ {F_x}\left( {{x_i}} \right) = \int_{ - \infty }^{{x_i}} {\int_{ - \infty }^\infty {f\left( {x,y} \right){\rm{d}}y} } {\rm{d}}x $$ (12) 式中：
${x_i}$ 为x方向坐标.y方向积分得到的电流时序曲线是
$$ {F_y}\left( {{y_i}} \right) = \int_{ - \infty }^{{y_i}} {\int_{ - \infty }^\infty {f\left( {x,y} \right){\rm{d}}x} } {\rm{d}}y $$ (13) 式中：
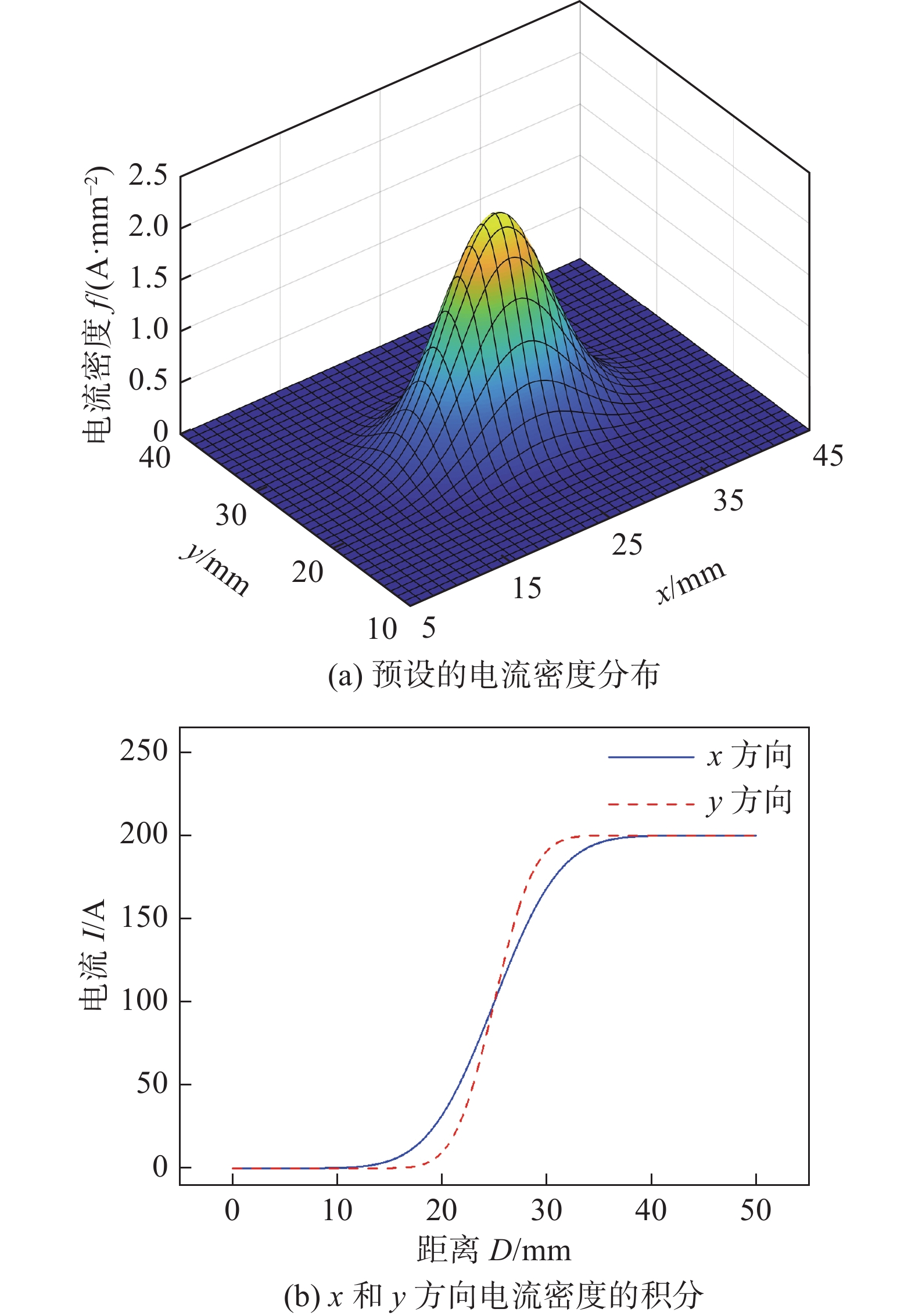
${y_i}$ 为y方向坐标.设定标准热源模型电流
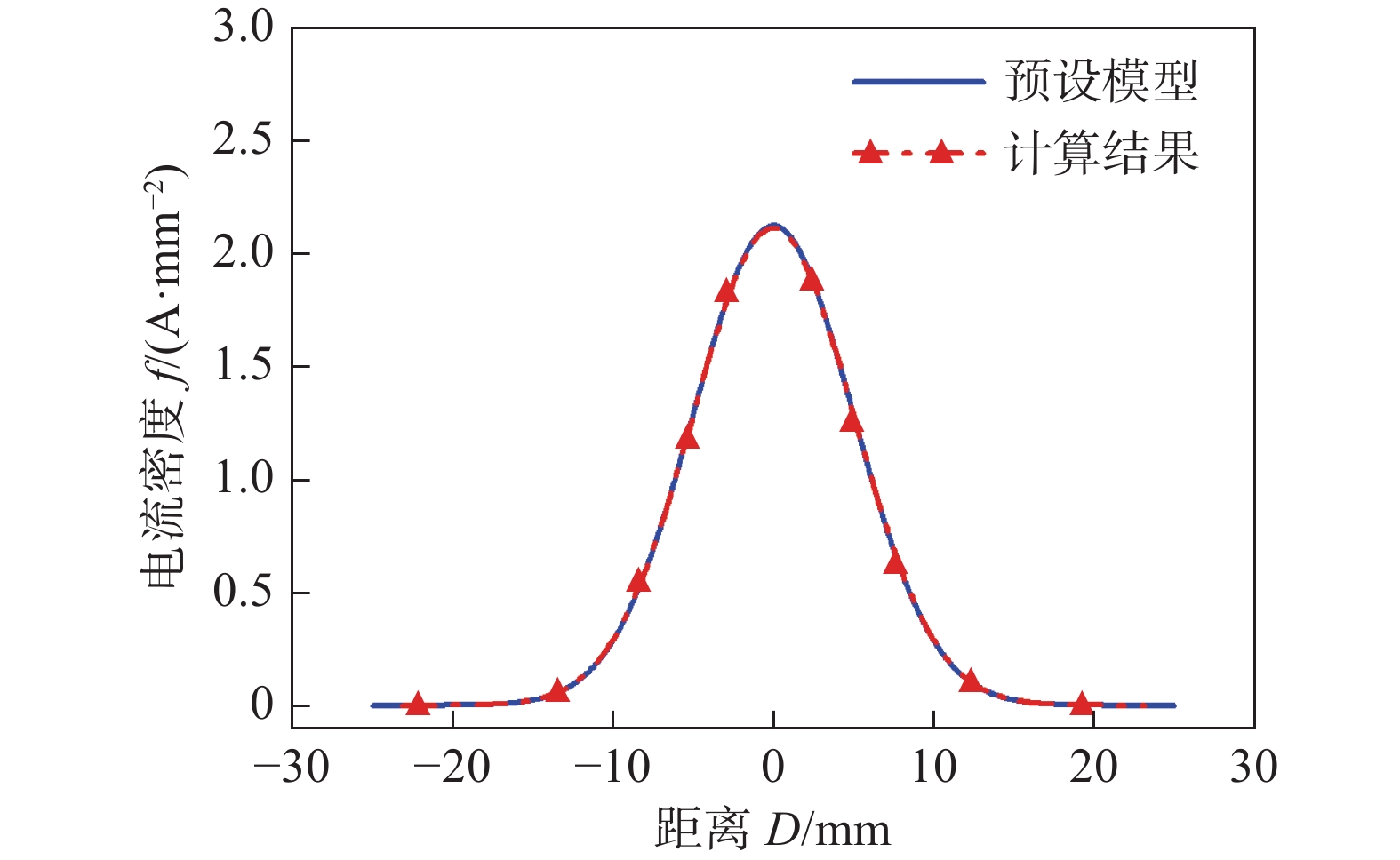
${{I}} $ = 200 A，${\sigma _1} = 5$ mm,${\sigma _2} = 3$ mm,${\mu _1} = 25$ mm，${\mu _2} = 25$ mm. 在x和y方向电流积分如图7所示.![]()
图 7 预设电流密度分布面模型Figure 7. Preset current density distribution model. (a) preset current density distribution; (b) current density integral on x and y directions采用分裂阳极新方法，计算电流密度分布，校验修正后的分裂阳极法对阳极电流密度的测量计算的效果，计算结果如图8所示，计算结果表明，采用修正后的分裂阳极法，能高精度的实现类似椭圆分布的电弧阳极电流密度测量.
![]()
图 8 预设热源模型的分裂阳极法计算结果(x方向)Figure 8. Calculation result by split anode method for preset model (x direction)3. 讨论
3.1 信号降噪处理
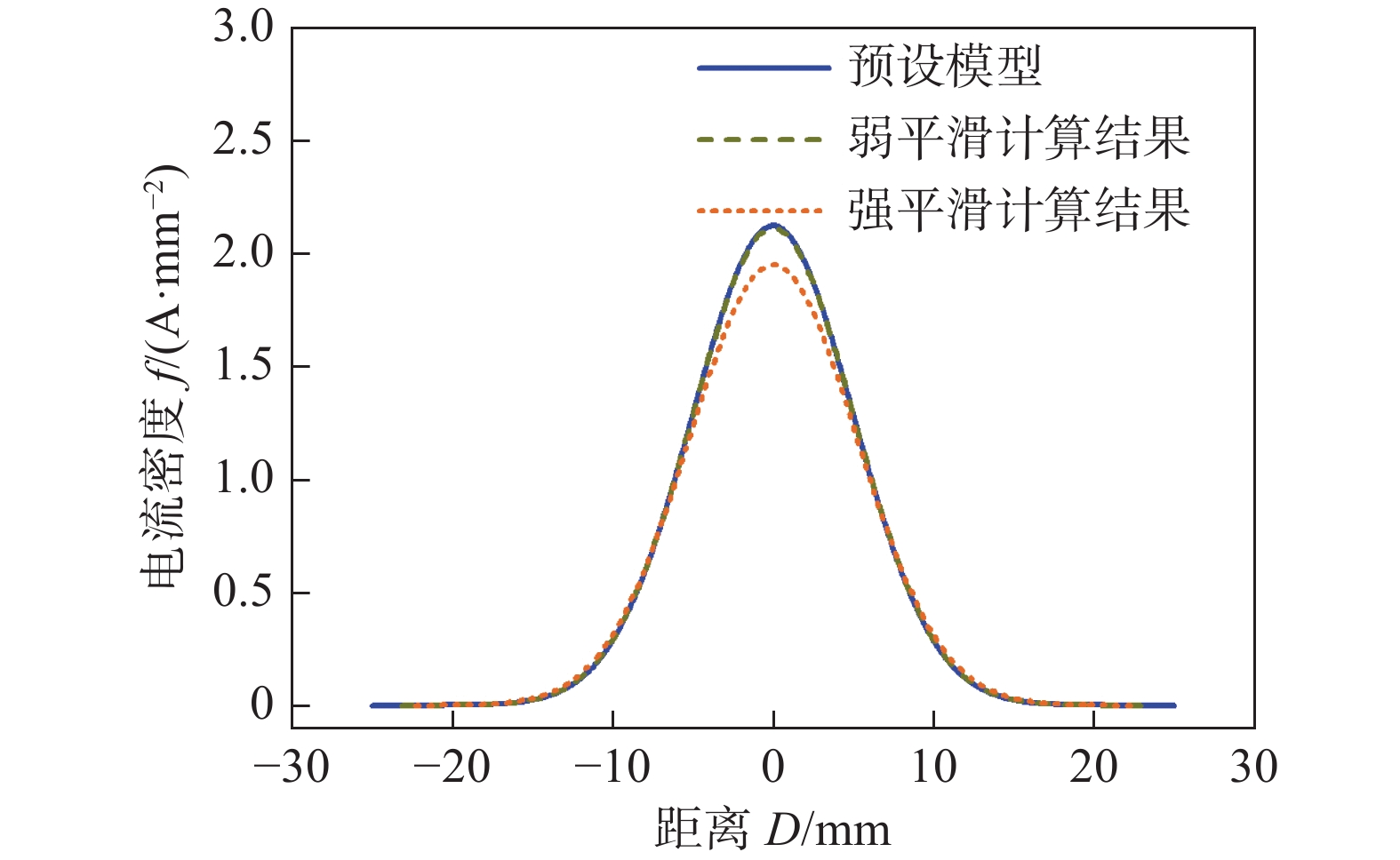
预设的阳极电流密度为理想化的二维高斯分布，忽略了信号噪声等干扰因素. 然而在实际测量过程中，由于噪声信号、电弧拖尾的存在，电弧阳极电流密度分布并非理想化的类似椭圆分布，在分裂阳极法计算过程中，需要对电流序列信号进行多次平滑. 采用不同的平滑强度，模拟分裂阳极计算过程中的电流序列信号平滑强度，计算不同平滑强度对修正后的分裂阳极法计算效果的影响，结果如图9所示，可以看出，平滑强度对阳极电流密度计算结果存在一定影响. 而实际的测量过程中，由于原始电信号噪声的存在，在进行数据微分计算时信号必须经过降噪处理.
![]()
图 9 不同平滑程度的修正后分裂阳极法计算结果(x方向)Figure 9. Calculation results by modified split anode method with different smoothness degree(x direciton)3.2 非柱对称侧向压缩等离子弧电流密度测量
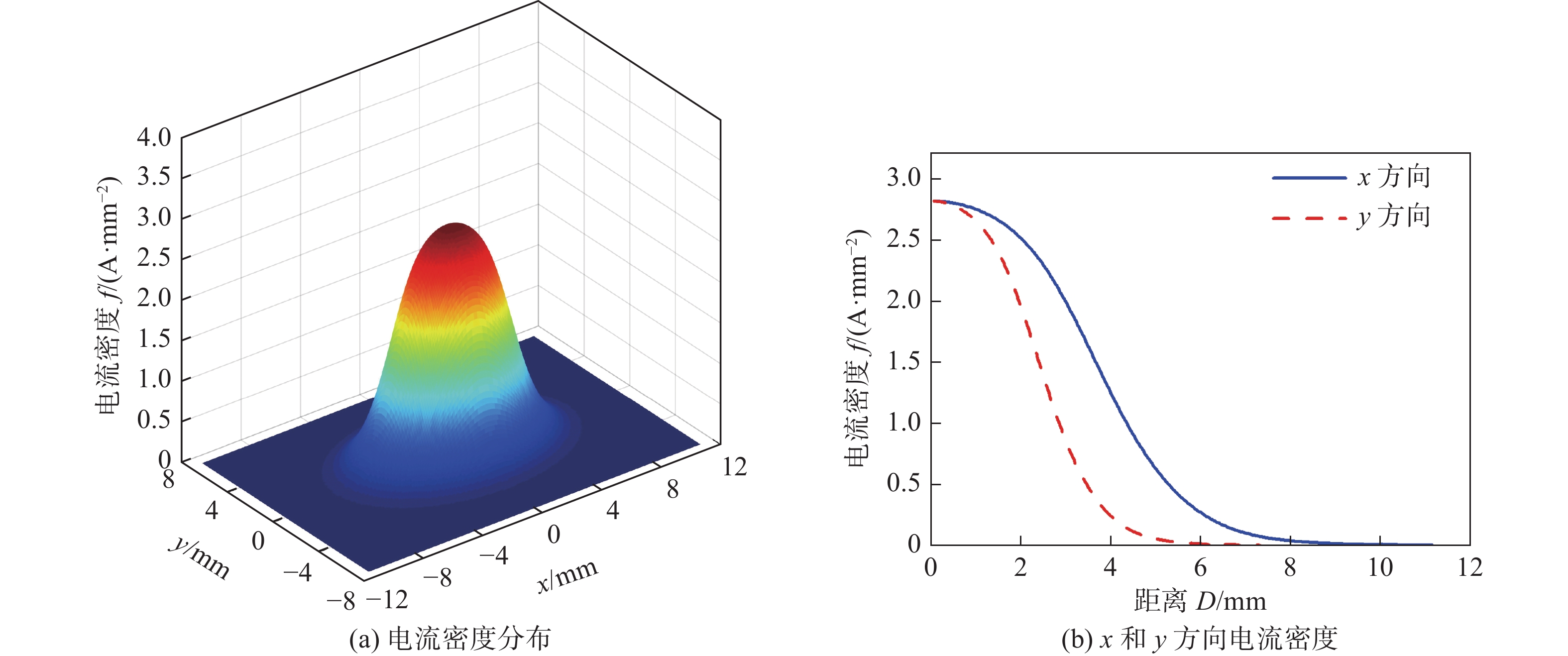
非柱对称分布的旁孔侧向压缩等离子弧后，改变等离子弧能量和电弧力分布. 采用修正后的分裂阳极计算不同常规等离子弧和非柱对称侧向压缩等离子弧阳极电流密度分布. 测量时焊接电流为100 A，离子气流量为3.5 L/min，阳极为水冷铜块，离子气和保护气均为氩气. 测量得到的非柱对称侧向压缩等离子弧阳极电流密度分布如图10所示，最大电流密度为2.8 A/mm2，电弧阳极电流密度的分布在x和y方向的差异较大，y方向收缩明显，为非柱对称分布.
![]()
图 10 侧向压缩的非柱对称等离子弧阳极电流密度分布Figure 10. Anode current density distribution of non-axisymmetric side-compressed plasma arc. (a) current density distribution; (b) current density distribution in x and y directions4. 结论
(1) 在分裂阳极的基础上，提出采用两次运动方向垂直的分裂阳极测量，计算非柱对称电弧阳极电流密度的新方法.
(2) 与常规分裂阳极法相比，修正后的分裂阳极新方法不再将电弧为柱对称结构作为电流密度测量的约束条件.
(3)采用修正后的分裂阳极法，实现了非柱对称侧向压缩等离子弧阳极电流密度的测量. 与x方向相比，电弧阳极电流密度在y方向压缩明显，呈现典型非柱对称分布.
-
![]()
图 3 常规分裂阳极法圆环分割示意图
Figure 3. Schematic diagram of ring division for conventional split anode method
![]()
图 7 预设电流密度分布面模型
Figure 7. Preset current density distribution model. (a) preset current density distribution; (b) current density integral on x and y directions
![]()
图 8 预设热源模型的分裂阳极法计算结果(x方向)
Figure 8. Calculation result by split anode method for preset model (x direction)
![]()
图 9 不同平滑程度的修正后分裂阳极法计算结果(x方向)
Figure 9. Calculation results by modified split anode method with different smoothness degree(x direciton)
-
[1] Das A, Kumar A, Shankhwar K, et al. A review of heat source and resulting temperature distribution in arc welding[J]. Journal of Thermal Analysis and Calorimetry, 2022, 147(23): 12975 − 13010. doi: 10.1007/s10973-022-11589-w
[2] Cho W I, Na S J. Impact of driving forces on molten pool in gas metal arc welding[J]. Welding in the World, 2021, 65(9): 1735 − 1747. doi: 10.1007/s40194-021-01138-8
[3] 郭力玮, 黄继强, 冯音琦, 等. 环境压力对GMAW电弧能量耗散的影响[J]. 焊接学报, 2022, 43(2): 61 − 66. Guo Liwei, Huang Jiqiang, Feng Yinqi, et al. Effect of ambient pressure on energy dissipation of GMAW arc[J]. Transactions of the China Welding Institution, 2022, 43(2): 61 − 66.
[4] Farias R M, Teixeira P R F, Vilarinho L O. Variable profile heat source models for numerical simulations of arc welding processes[J]. International Journal of Thermal Sciences, 2022, 179: 107593. doi: 10.1016/j.ijthermalsci.2022.107593
[5] Chen G, Williams S, Ding J, et al. Split anode calorimetry for plasma arc energy density measurement with laser calibration[J]. Journal of Manufacturing Processes, 2022, 78: 71 − 81. doi: 10.1016/j.jmapro.2022.04.003
[6] Nestor O H. Heat intensity and current density distributions at the anode of high current, inert gas arcs[J]. Journal of Applied Physics, 1962, 33(5): 1638 − 1648. doi: 10.1063/1.1728803
[7] Shih K T. Anode current density in high‐current pulsed arcs[J]. Journal of Applied Physics, 1972, 43(12): 5002 − 5005. doi: 10.1063/1.1661060
[8] 张勤练. 柔性变极性等离子弧特性及铝合金横焊穿孔熔池行为[D]. 哈尔滨: 哈尔滨工业大学, 2017. Zhang Qinlian. Characteristics of soft variable polarity plasma arc and behavior of molten pool with keyhole in aluminum alloy horizontal position welding[D]. Harbin: Harbin Institute of Technology, 2017.
[9] 李钊, 杨春利, 范成磊, 等. 新型变极性等离子弧横焊热-力特性及成形研究[J]. 机械工程学报, 2017, 53(16): 156 − 162. doi: 10.3901/JME.2017.16.156 Li Zhao, Yang Chunli, Fan Chenglei, et al. Research on new heat source model of variable polarity plasma arc and welding forming in horizontal position[J]. Journal of Mechanical Engineering, 2017, 53(16): 156 − 162. doi: 10.3901/JME.2017.16.156
[10] Chen S, Jiang F, Lu Z, et al. Measurement and analysis of the welding arc current density and pressure distribution based on split anode method[C]//2011 IEEE International Conference on Mechatronics and Automation, Mechatronics and Automation (ICMA), 2011 International Conference On. August, 2011: 1544 − 1549.
[11] Egerland S, Colegrove P A, Williams S W. Investigation of low current gas tungsten arc welding using split anode calorimetry[J]. Science & Technology of Welding & Joining, 2017, 22(1): 71 − 78.
[12] Zhao H, Yang C, Fan C. Research of a novel non-axisymmetric side-compressed variable polarity plasma arc and its pressure distribution characteristics[J]. Metals, 2024, 14(2): 231. doi: 10.3390/met14020231
-
期刊类型引用(1)
1. 伏承炜，侯国清，马蓉，李渊博. TIG电弧电流密度分布研究现状和进展. 焊管. 2025(05): 9-17 . 
百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 268
- HTML全文浏览量: 39
- PDF下载量: 75
- 被引次数: 1
