Fatigue life assessment of load-carrying 60° oblique cruciform full-penetration welded joints
-
摘要:
为研究承载型60°斜十字全熔透焊接接头 (oblique cruciform full-penetration welded joints,OCFWJs)局部应力分布及疲劳性能,设计3个试验模型完成3种名义应力幅水平下的疲劳试验,得到试件疲劳破坏时的循环次数. 利用ABAQUS软件建立60° OCFWJs有限元模型,计算得到焊趾处热点正应力、热点剪应力及等效热点应力. 基于规范中的名义应力S-N曲线和热点应力S-N曲线,分别采用名义主应力法、等效热点应力法和相互作用方程方法对拉—剪联合作用下60° OCFWJs疲劳寿命进行了评估. 结果表明,采用名义应力幅、名义拉应力幅或名义剪应力幅均无法对60° OCFWJs疲劳寿命进行可靠评估. 依据国际焊接学会(International Institute of Welding,IIW)规范无论采用热点拉应力幅或热点剪应力幅也无法对60° OCFWJs疲劳寿命进行可靠评估. 按欧洲钢结构设计规范Eurocode3相互作用方程方法预测的疲劳寿命远低于试验值,按等效热点应力方法预测的疲劳寿命与试验值符合良好.
Abstract:To study the local stress distributions and fatigue performance of load-carrying 60° oblique cruciform full-penetration welded joints (OCFWJs), three test specimens were designed for fatigue tests under three nominal stress amplitude levels, and the numbers of loading cycles until fatigue failure of the specimens were obtained. Using ABAQUS finite element software, the finite element models of 60°OCFWJs were established, and the hot spot normal stress, hot spot shear stress, and equivalent hot spot stress at the weld toe were calculated. Based on the nominal stress S-N curves and the hot spot stress S-N curves defined in the specifications, the fatigue life of 60° OCWJs under the combined action of tensile and shear stress were evaluated by using the nominal principal stress method, the equivalent hot spot stress method, and the interaction equation method, respectively. The results showed that whether the nominal stress range, the nominal tensile stress range, or the nominal shear stress range were used, the fatigue life of 60° OCWJs couldn't reliably evaluated. According to the International Institute of Welding specification, whether the hot spot tensile stress ranges or the hot spot shear stress ranges couldn't be used to evaluate the fatigue life of 60° OCFWJs reliably. The fatigue lives predicted by the interaction equation method in Eurocode 3:Design of Steel Structures were much lower than the experimental values , and the fatigue lives predicted by the equivalent hot spot stress method were in good agreement with the experimental values .
-
0. 序言
法兰圆片是旋片阀中主要的真空部件. 在装配过程中,上下法兰圆片与围壁之间的安装很容易受到法兰径向弯曲的影响,从而降低了旋片阀的真空性能. 而法兰与水冷圈之间的焊接过程是导致径向变形的主要原因,所以如何有效降低焊接变形具有研究意义.
焊接过程是一个复杂的物理化学过程. 在焊接加热过程中,焊缝及附近区域因受热膨胀而受到周围温度较低区域金属的约束,产生压缩塑性应变,冷却后残余压缩塑性应变就决定了残余应力和变形[1-2]. 焊接变形会直接导致焊件的制造精度、装配精度和结构性能的降低. 传统的对于变形的预测方法都是基于试验和经验公式法,不仅耗时耗力,而且预测精度也不高. 随着弹塑性理论的提出以及计算机软硬件的飞速发展,基于热力耦合的热弹塑性数值模拟方法已经成为研究焊接过程的最普遍方法.
众多学者通过建立合理的计算模型以及试验测试方法来研究外拘束对焊件变形的影响,并且绝大部分结果表明外加拘束对焊接变形影响显著. Liu等人[3]研究了外拘束对薄板坯连铸节点变形的影响,分析得出在屈曲变形之前,拘束可一定程度上减小变形量. Liang等人[4]通过固有应变和界面元法研究曲线加筋板的变形,并指出热输入、外部拘束、焊接顺序对其最终变形有显著影响. 马国等人[5]对比四种拘束状态下焊件的变形情况,发现弹簧拘束和接触拘束与试验较为吻合,且弹簧拘束误差最小. Wahab等人[6]通过试验提出施加在焊件上的拘束力是动态变化的,在此基础上,Liu等人[7]对不同初始拘束力以及拘束位置进行了研究,得出了不同拘束条件释放前后的变形规律. Mao等人[8]采用两种不同的约束方式控制焊件的变形,对比可得三维多场耦合模型更加贴近试验结果,且应变范围较小. 然而目前关于外拘束的研究较少,且只对个别因素进行了探究,所以为了更全面探究法兰的径向变形情况,文中从拘束刚度、初始拘束力、拘束距离以及拘束宽度4个方面来对焊件交叉多层多道焊进行研究,分析4个因素对变形量影响的规律.
1. 试验过程
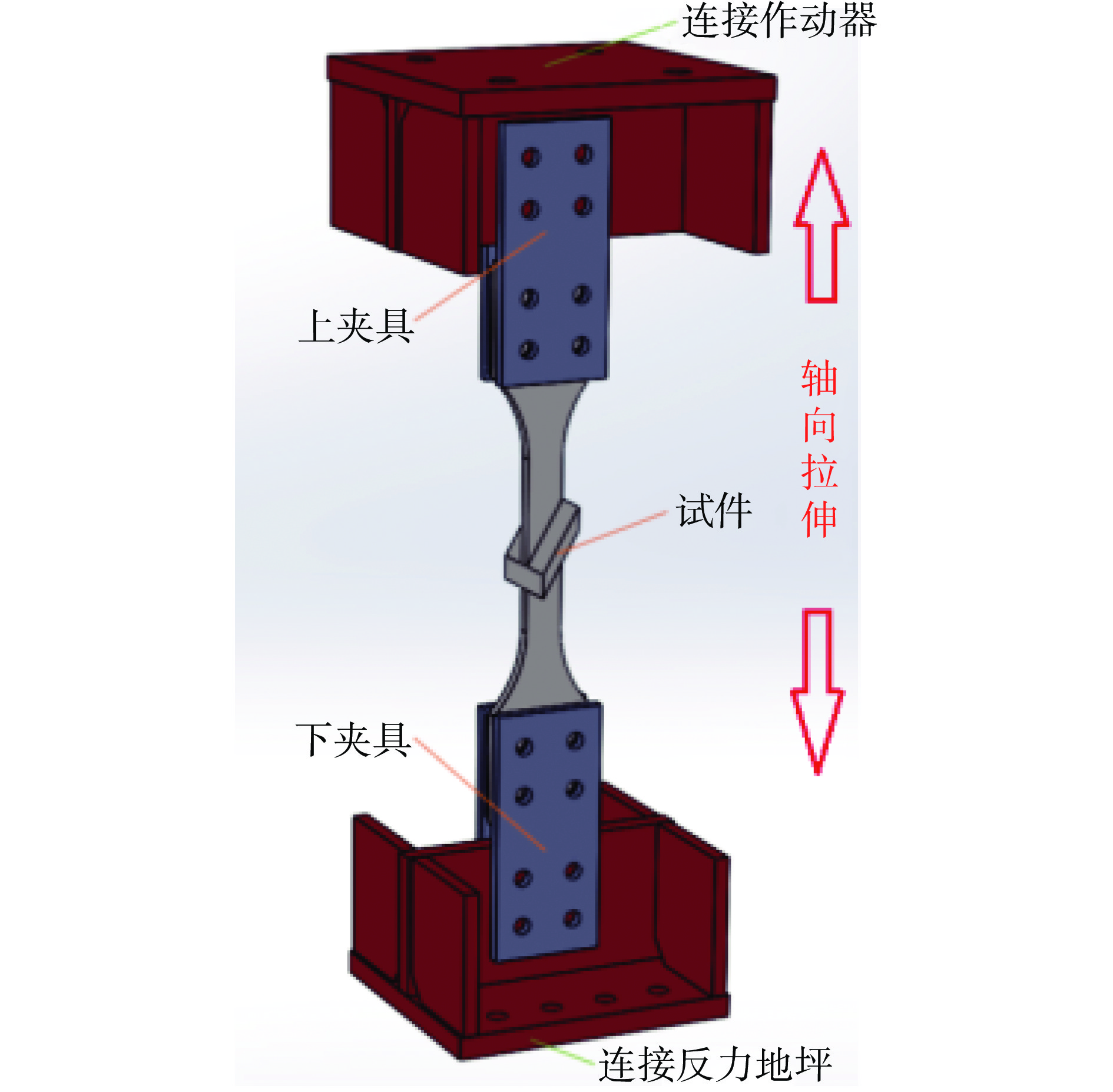
试验材料为SUS304钢,采用氩气为保护气体的非熔化极气体保护焊(TIG)对两条焊缝进行填充,焊接方式为交互多层多道焊,两条焊缝的相应焊道焊接参数相同. 焊件分别为内外圈直径分别为393,520 mm的环形法兰以及直径为450 mm的环形水冷圈,内外环向焊缝的直径分别为408,419 mm. 分三组进行试验:第一组测量自由状态下A点厚度方向的位移变化;第二组在第一组的基础上限制了焊件底部沿厚度方向的位移;第三组在第一组的基础上添加了沿法兰外边缘的环向夹具,且沿径向的宽度为10 mm. 焊接顺序以及1/12焊件示意图如图1所示.
焊丝的型号为ER308,依据不同焊道分别采用直径1.2,1.6和2.0 mm,焊接所采用的电弧电压、焊接电流、焊接速度如表1所示.
表 1 焊接工艺参数Table 1. Welding parameters道次 电弧电压
U/V焊接电流
I/A焊接速度
v/(m·s−1)焊丝直径
ϕ/mm第一道 11 176 0.003 1.2 第二道 12 178 0.003 1.2 第三道 14 182 0.003 1.6 第四道 14 182 0.003 2.0 由于焊接过程是准热稳态过程,除起焊和止焊端,各个横截面沿焊件厚度方向的变形应该相一致,所以通过测量A点在厚度方向的变形量来表征焊件外边缘沿厚度方向的变形情况. 每次焊接总历时约为5723 s,共8道焊,每道之间冷却时间为10 min.图2显示了施加压板夹具的试验现场.
2. 有限元数值模型分析
采用基于热力耦合的热-弹-塑有限元法对焊件进行分析. 首先通过对焊接热输入的模拟计算获得多道焊瞬态温度场,其次在弹-塑性分析中,考虑材料的高温物理性能以及力学性能为非线性. 温度场计算忽略相变的影响,并假设熔敷金属与母材的高温材料性能相同.
2.1 温度场计算模型
焊接热输入探究中,有学者对TIG的热源模型适用性进行研究[9],结果表明双椭球热源模型的效果最好,故采用该热源模型进行研究,各焊道的椭球尺寸参数通过试验测得. 由于实际焊缝形状是环向,所以经过变换可得环向双椭球热源模型为
$$ \left\{ \begin{array}{l} {q_{\rm{f}}}(x,y,{\textit{z}}) = \dfrac{{6\sqrt 3 {f_{\rm{f}}}Q}}{{{a_{\rm{f}}}bc{{\text{π}} ^{3/2}}}}\exp \left[\dfrac{{ - 3{{(y\cos \alpha - x\sin \alpha )}^2}}}{{a_{\rm{f}}^2}}\right]\exp \left[\dfrac{{ - 3{{(x\cos \alpha + y\sin \alpha )}^2}}}{{b_{}^2}}\right]\exp \left[\dfrac{{ - 3{{({\textit{z}} - {{\textit{z}}_0})}^2}}}{{{c^2}}}\right]\\ {q_{\rm{r}}}(x,y,{\textit{z}}) = \dfrac{{6\sqrt 3 {f_{\rm{r}}}Q}}{{{a_{\rm{r}}}bc{{\text{π}} ^{3/2}}}}\exp \left[\dfrac{{ - 3{{(y\cos \alpha - x\sin \alpha )}^2}}}{{a_{\rm{r}}^2}}\right]\exp \left[\dfrac{{ - 3{{(x\cos \alpha + y\sin \alpha )}^2}}}{{b_{}^2}}\right]\exp \left[\dfrac{{ - 3{{({\textit{z}} - {{\textit{z}}_0})}^2}}}{{{c^2}}}\right] \end{array} \right. $$ (1) 式中:qf ,qr分别为前半椭球和后半椭球的热生成率;Q为焊接热输入;ff,fr为热源模型前后半球的能量分配系数;af ,ar ,b,c为双椭球热源形状参数;z0为焊道距离工作台的高度;α为焊点与法兰中心轴连线扫过的角度.
考虑焊件与空气的对流换热以及辐射换热,并且在真空通道区域降低换热系数,不考虑母材与工作台、夹具之间的传热.
2.2 动态拘束有限元模型
由于大型焊件数值模拟耗时耗力,考虑到焊件为中心对称模型且焊接的准热稳态特性,为节约计算成本,分别选取1/16,1/12,1/8,1/4的原焊件模型进行仿真试算. 结果显示1/12,1/8,1/4模型的模拟结果具有准热稳态过程且该过程中变形大小一致,为了节约计算成本,采用1/12原焊件模型作为仿真模型. 在焊接过程中,焊件局部材料不均匀的膨胀收缩会导致焊件产生变形,较低刚度的夹具也会随之发生变形从而导致其施加到焊件上的力发生变化,但由于变形量微小,所以在小范围内将夹具夹紧力的变化视为线性变化. 刘川等人[10]通过弹簧单元模拟夹具的动态拘束并成功得出了焊件在外拘束情况下的变形趋势,验证了弹簧单元模拟的可行性. 所以文中采用弹簧单元来模拟夹具的刚度效果,弹簧的一端与压板通过位移耦合连接在一起,另一端施加初始位移来模拟初始夹紧力.
在多场耦合分析过程中,建立尺寸比例为1∶1的多场耦合模型,考虑焊件与工作台为柔性-刚性面接触,焊件和夹具之间采用柔性-柔性面接触. 由于变形量较小,所以不考虑焊件与夹具之间相对位移带来的摩擦影响. 限制焊件内圈的周向自由度,以及完全约束工作台的自由度. 建立的动态拘束有限元模型如图3所示,共7 215个网格.
图4表示4个动态拘束的因素中,弹簧单元的弹性模量表示为拘束刚度;弹簧单元的初始位移表示为初始拘束力;压板与外侧焊缝的径向距离表示为拘束距离;压板沿径向方向的长度表示为拘束宽度.
2.3 回归分析
为了分析影响焊接变形的4个动态拘束因素的主次程度,文中采用基于最小二乘法模型的多元线性回归分析,位移量作为因变量,4个动态拘束因素作为自变量.
$$ Y = {w^T}X + b $$ (2) 式中:
$X = {\left({x_1},{x_{2,}} \cdots,{x_n}\right)^T}$ 表示共有的样本量,其中$x = {\left({x^1},{x^2},{x^3},{x^4}\right)^T}$ 中${x^i}$ 代表该样本的第$i$ 个特征;$w = {\left({w^1},{w^2},{w^3},{w^4}\right)^T}$ 表示各特征因素的权重;$b$ 代表$Y$ 不受$X$ 影响的部分;$Y$ 表示位移量. 为了消除不同量纲带来的影响,故在回归之前对各因素进行标准化处理.回归分析的作用主要体现在3个方面:识别4个拘束因素中的重要变量;判别拘束变量与位移量之间的相关方向;在各变量表现显著的条件下估计自变量的权重. 其作用倾向于解释型回归而不是预测型回归,所以更加关注各变量的显著程度以及
$w$ 的大小,而不关注拟合优度${R^2}$ 的大小. 故目标函数表示为$$ g(w,b) = \sum\limits_{i = 1}^n {{{\left({w^T}{x_i} + b - {y_i}\right)}^2}} $$ (3) 矩阵的求解公式由此推导为
$$ {w^T} = {\left({X^T}X\right)^{ - 1}}{X^T}Y $$ (4) 3. 数值模拟及试验结果
3.1 焊件试验结果
图5表示三组试验法兰上表面中心线沿厚度方向的变形情况,其横坐标代表测量点离焊件内环的径向距离. 三组试验的变形量趋势相一致,第二组为刚性拘束,在释放拘束之后,焊件的回弹量较大. 而通过施加夹具对沿厚度方向变形的抑制效果最好,边缘变形量为0.22 mm.
图6表示中截面A点沿厚度方向在整个焊接过程的位移曲线,可见焊接过程中第5,7道焊后变形量最大,主要由于最后四道焊的热输入量增加,加上其靠近内圈,截面沿厚度方向的变形反馈至外围导致变形量较大. 其最终变形量对比试验获取的数据,可见模拟效果较好,并体现了利用弹簧单元模拟夹具动态拘束的可行性.
3.2 各拘束因素对焊接变形的影响
3.2.1 拘束刚度对焊接变形的影响
基于弹簧单元模拟夹具的拘束行为,利用弹簧单元的弹性模量来表示拘束刚度,下文均以A点沿厚度方向的位移为表述对象,即横截面外边缘沿厚度方向的变形情况.图7表示拘束位置距离外圈焊缝为27 mm、拘束长度沿径向为10 mm情况下的三条曲线. 由图可见,较小刚度区域内位移量降低迅速,随着弹性模量不断增加,其变化率逐渐降低并趋于平缓,当刚度达到20 kN/mm时,释放后的变形量仅有0.06 mm.
焊接遵循着变形越小应力越大的规律,较高的刚度拘束导致较大内应力,外拘束的释放带来应力的释放,从而导致回弹量的产生. 随着刚度的增加,回弹量也逐渐增加且趋于平缓,当刚度为20 kN/mm时,回弹量为0.028 8 mm.
3.2.2 初始夹紧力对焊接变形的影响
在夹具固定过程中如果施加一定的夹紧力,焊件的变形量会进一步减小.图8在图7的基础上选定0.2,0.5和1 kN/mm 3个不同刚度情况下去探讨初始力大小对于变形量的影响. 曲线趋势表现一致,均为位移量随着初始力的增加而降低且降低速率由快到慢. 当初始力达到1 kN时,三种刚度下对应的位移分别只有0.016,0.014和0.013 mm.
对比图中的三条曲线,可知在较低刚度条件下,同等初始力的拘束效果明显于较高的刚度条件,且随着刚度的不断增加而初始力的效果不断减弱.
3.2.3 拘束距离对焊接变形的影响
考虑到拘束远离焊缝中心的位置会对最终的变形量产生影响,结合生产实际,夹具的拘束最小的施加距离为远离外侧焊缝12 mm,并且以2.5 mm为间隔作为计算样本,最远距离不超过27 mm.
从图9可见零初始力不同刚度拘束的作用下,位移量几乎都随着距离的增加呈现线性减小的趋势. 且变化率在低刚度以及高刚度范围下较小,中间区域略大,呈现先增后减并趋于稳定的趋势,如图10所示. 这是由于在低刚度条件下拘束能力较弱,能够拘束的变形量较小,拘束位置的变动所带来的影响也就很小. 但随着刚度的增加,其效果会迅速增加,并在刚度约为0.6 kN/mm时位移变化率达到最高为0.017 56. 而较高刚度的拘束使得位移控制在很小的范围,同样也会减弱拘束位置对其影响作用.
3.2.4 拘束宽度对焊接变形的影响
拘束宽度和其它的因素具有相关性,结合实际情况,在同一拘束条件下,总刚度以及初始拘束力随着拘束宽度的增减而等比增减. 由于尺寸限制,最大拘束宽度不超过20 mm. 拘束宽度和拘束距离之和小于等于外侧边缘与外侧焊缝之间的距离.
图11表示四种刚度零初始力拘束下的位移曲线,小刚度拘束条件下位移的变化更趋向于线性,随着刚度增加,其非线性趋势愈加明显,但都表现为位移降低速率由快到慢,并在一定的拘束宽度后趋于平缓. 同时,对比图中4条曲线,刚度条件越大,位移曲线随着拘束宽度的增加就越快趋于平缓.
3.3 回归分析结果
在实际焊件允许的自变量取值范围内,经过共69组的数值模拟,部分结果如表2所示.通过对上表中的样本进行基于最小二乘法的回归分析,得到拘束刚度、初始力、拘束宽度比、拘束距离4个变量对位移量的影响情况.表3为各自变量的标准化回归系数,结果可见无论各因素是否经过标准化处理,其回归系数皆为负数,表明各因素数值的增加都会导致变形量的减小,验证了上文的数值模拟结果. 在95%的置信区间下,只有拘束刚度、初始力、拘束宽度比的P值小于0.05,代表其回归系数显著的异于0,代表这3个因素对变形量的影响较为显著. 而拘束距离的P值0.557无法拒绝原假设,所以不具备显著性.
表 2 部分数值模拟结果Table 2. Part of numerical simulation results拘束刚度$K/({\rm{kN} } \cdot {\rm{m{m^{ - 1} } } } )$ 初始力${F_0}/{\rm{kN} }$ 拘束宽度$d/{\rm{mm}}$ 拘束距离$L/{\rm{mm}}$ 位移${u_{\textit{z} } }/{\rm{mm}}$ 0 0 10 27 1.406 69 0.2 0 10 27 1.152 2 0.5 0 10 27 0.787 503 1 0 10 27 0.510 7 3 0 10 27 0.270 974 0.2 0.2 10 27 0.478 729 0.2 0.5 10 27 0.194 276 0.2 1 15 27 0.015 8 ...... 3 0.5 5 12 0.251 768 3 0 10 12 0.367 724 表 3 回归分析结果Table 3. Regression analysis results位移 系数 标准误差 t值 P > |t| 标准化系数 拘束刚度 −0.055 4 0.012 31 −4.5 0 −0.457 68 初始力 −0.815 8 0.129 51 −6.3 0 −0.640 5 拘束宽度比 −0.239 6 0.113 28 −2.12 0.04 −0.213 83 拘束距离 −0.003 8 0.006 41 −0.59 0.557 −0.059 95 常量 1.093 1 0.198 14 5.52 0 . 标准回归系数可知初始力的影响最显著,达到了−0.640 5,而拘束位置只有−0.059 95,其影响性较其它3个因素小很多. 所以在研究各因素与位移量的相关关系时,可忽略拘束距离对位移带来的影响.
3.4 试验验证
针对拘束初始力对焊接变形的影响最为显著,分别选取初始力大小为0.1, 0.5,1.0 kN,拘束刚度为1.0 kN/mm,拘束宽度为10 mm,拘束距离为27 mm情况下焊件上表面中心线处沿厚度方向的变形量进行验证. 由图12可见模拟效果较好,与试验结果吻合度较高. 拘束初始力越大,外拘束对焊件变形量的限制越强,数值模拟和试验之间的精度就越高. 在0.5 kN的初始力下,焊件边缘沿厚度方向的变形量能够控制在0.15 mm左右,而在1.0 kN的初始力下,几乎可以忽略变形量的大小.
4. 结论
(1)动态拘束相较于刚性拘束能够更好的减小法兰片焊后的变形量.
(2)拘束的释放导致法兰片发生回弹,且回弹量随着拘束刚度的增加而增加. 在刚性拘束下,回弹量接近1.0 mm.
(3)随着拘束刚度、拘束初始力、拘束宽度、拘束距离的任一因素的增加,法兰片的沿厚度方向的变形量都会减小. 其中前3个因素下变形量的减小呈现由快到慢的趋势,并最终趋于平缓.
(4)拘束刚度、拘束初始力、拘束宽度对于法兰片变形量的影响比较显著,且其影响程度由大到小分别为拘束初始力、拘束刚度、拘束宽度. 所以在焊接过程中,施加较大的初始夹紧力以及采用较高刚度的夹具能够更加有效的控制其沿厚度方向的变形.
(5)拘束初始力超过0.5 kN时,法兰片边缘沿厚度方向变形量能控制在0.15 mm之内,而在超过1.0 kN时,可忽略焊接带来的变形影响.
-
表 1 名义应力幅及疲劳寿命
Table 1 Nominal stress range and fatigue life
试件 最大荷载
Fmax/kN最小荷载
Fmin/kN名义应力幅
Δσnom/MPa实测疲劳寿命
Nt/104周次B1 220 22.0 247.0 24.7995 B2 136 13.6 153.0 88.9259 B3 172 17.2 193.5 33.0092 表 2 不同的名义应力幅
Table 2 Different nominal stress amplitudes
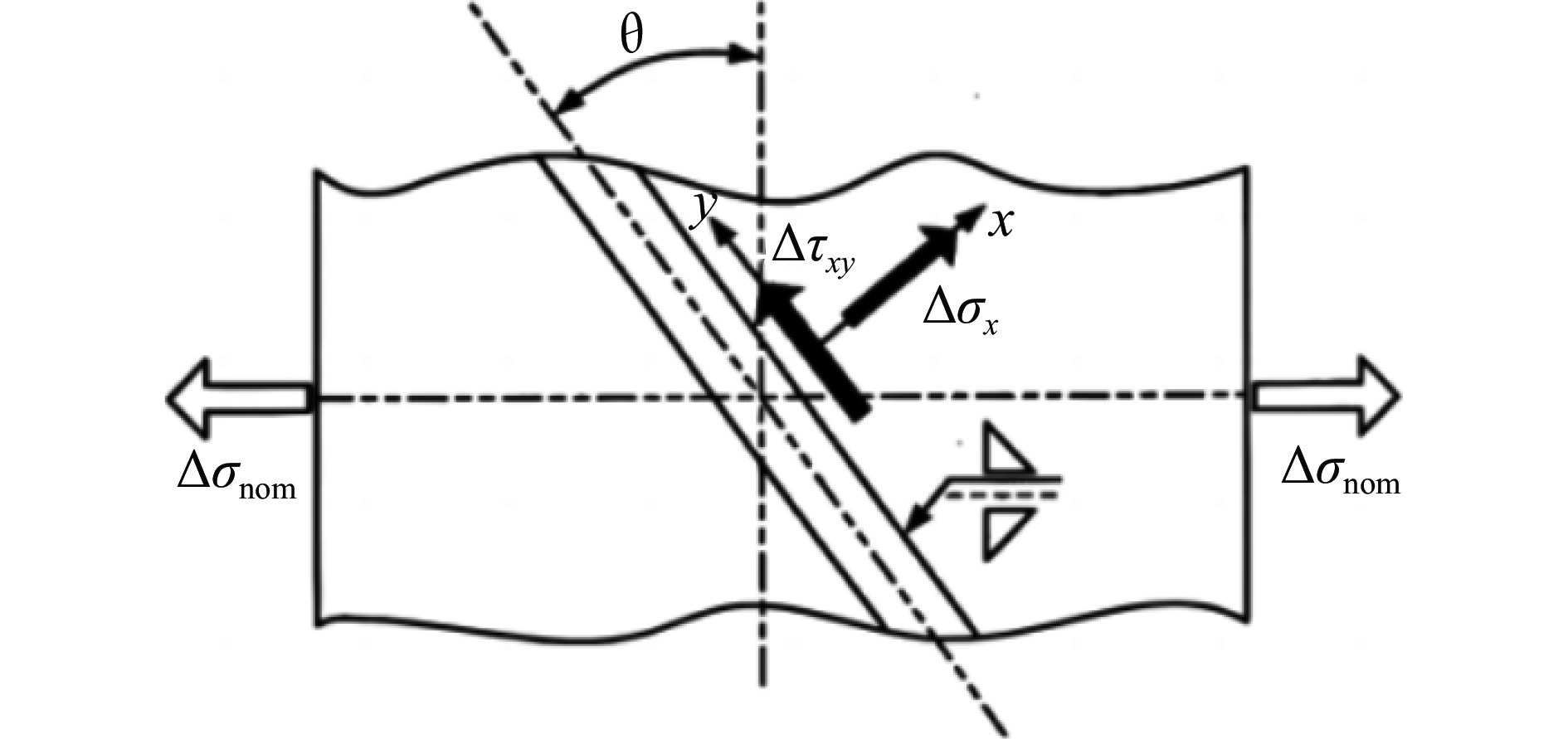
名义应力幅
Δσnom/MPa名义正应力幅
Δσx/MPa名义剪应力幅
Δτxy/MPa最大主应力幅
Δσ1/MPa153.0 38.25 66.25 88.08 193.5 48.38 83.79 111.40 247.0 61.75 106.95 142.19 表 3 焊趾处的热点应力幅及疲劳寿命
Table 3 Hot spot stress range at the weld toe and fatigue life
试件 正应力幅
Δσx/MPa剪应力幅
Δτxy/MPa热点正应力幅
Δσh/MPa热点剪应力幅
Δτh/MPa等效热点应力幅
Δσhe/MPa基于Δσhe
疲劳寿命计算值
Nc1/104周次实测循环次数
Nt/104周次距焊趾
0.4 t距焊趾
1.0 t距焊趾
0.4 t距焊趾
1.0 tB1 71.4 66.0 199.1 197.7 75.02 200.04 213.64 20.5107 24.7995 B2 44.2 40.9 123.5 120.6 46.41 125.44 133.75 83.5889 88.9259 B3 55.9 51.7 156.0 152.6 58.71 158.28 168.82 41.5679 33.0092 表 4 基于最大主应力幅的疲劳寿命
Table 4 Fatigue life based on Δσ1
试件 最大主应力幅
Δσ1/MPa基于Δσ1疲劳寿命计算值
Nc2/104周次实测循环次数
Nt/104周次B1 142.19 35.6199 24.7995 B2 88.08 150.1093 88.9259 B3 111.40 74.0703 33.0092 表 5 基于相互作用方程法的疲劳寿命
Table 5 Fatigue life based on the interaction equation method
试件 热点正应力
$ \Delta {\sigma }_{\mathrm{h}} $/MPa热点剪应力
$ \Delta {\tau }_{\mathrm{h}} $/MPa疲劳寿命
Nc3/104周次实测循环次数
Nt/104周次B1 75.02 200.04 6.1625 24.7995 B2 46.41 125.44 62.3867 88.9259 B3 58.71 158.28 19.7306 33.0092 -
[1] 马景平, 曹睿, 周鑫. 高强钢焊接接头疲劳寿命的提高方法进展[J]. 焊接学报, 2024, 45(10): 115 − 128. Ma Jingping, Cao Rui, Zhou Xin. Development on improving fatigue life of high strength steel welded joints[J]. Transactions of the China Welding Institution, 2024, 45(10): 115 − 128.
[2] Timar I, Arpad I W. Optimal design of the fillet weld fastening the wind turbine column[J]. China Welding, 2024, 33(3): 39 − 43.
[3] Xiao L, Wei X, Zhao J M, et al. Hot spot stress concentration factor of CFST T/Y joints based on modified equivalent thickness[J]. Structures, 2023(51): 910 − 925.
[4] 高杰, 鞠晓臣, 左照坤, 等人. 基于等效结构应力法的高强钢焊接结构低温主S-N曲线[J]. 船舶力学, 2024, 28(4): 571 − 581. doi: 10.3969/j.issn.1007-7294.2024.04.009 Gao Jie, Ju Xiaochen, Zuo Zhaokun, et al. Low temperature master S-N curve of high strength steel welded structure based on equivalent structural stress method[J]. Journal of Ship Mechanics, 2024, 28(4): 571 − 581. doi: 10.3969/j.issn.1007-7294.2024.04.009
[5] 宋威, 满铮, 徐杰, 等. 含错位效应十字焊接接头疲劳可靠性评估[J]. 焊接学报, 2023, 44(6): 20 − 26,34. Song Wei, Man Zheng, Xu Jie, et al. Fatigue reliability analysis of load-carrying cruciform joints with misalignment effects[J]. Transactions of the China Welding Institution, 2023, 44(6): 20 − 26,34.
[6] Song W, Man Z, Xu J, et al. Fatigue reliability assessment of load-carrying cruciform welded joints with undercuts and misalignments[J]. Fatigue & Fracture of Engineering Materials & Structures, 2024, 47(2): 511 − 531.
[7] Laher B , Buzzi C , Leitner M, et al. Effect of angular distortion and axial misalignment on the fatigue strength of welded and ground mild steel cruciform joints[J]. Welding in the World, 2024, 68(5): 1169 − 1186.
[8] 苏庆田, 沈翀. 错位缺陷对钢桥中厚板斜十字接头静力性能影响研究[J]. 桥梁建设, 2023, 53(5): 17 − 23. Su Qingtian, Shen Chong. Research on influence of staggering defects on static performance of thick plate skew cross joints in steel bridge[J]. Bridge Construction, 2023, 53(5): 17 − 23.
[9] Soligo M, Campagnolo A, Meneghetti G, et al. Misalignment factors to affect the fatigue of welded load-carrying joints[J]. International Journal of Fatigue, 2024, 178: 107996. doi: 10.1016/j.ijfatigue.2023.107996
[10] Bartsch H, Feldmann M. Fatigue strength of cruciform joints with weld imperfections: a comprehensive numerical study[J]. Engineering Failure Analysis, 2024, 157: 107866. doi: 10.1016/j.engfailanal.2023.107866
[11] Raftar H R, Ahola A, Lipiainen K, et al. Fatigue behavior of load-carrying cruciform fillet weld joints under variable amplitude load[J]. Journal of Constructional Steel Research, 2024, 215: 108559. doi: 10.1016/j.jcsr.2024.108559
[12] 魏国前, 郭子贤, 闫梦煜, 等. 基于Pavlou方法的焊接结构疲劳寿命预测[J]. 焊接学报, 2023, 44(9): 16 − 23. Wei Guoqian, Guo Zixian, Yan Mengyu, et al. Pavlou approach based fatigue life prediction for welded structures[J]. Transactions of the China Welding Institution, 2023, 44(9): 16 − 23.
[13] Wang W Z, Shi W Z, Li B, et al. High-cycle fatigue life assessment of welded cruciform joints of Q460D steel[J]. Structures, 2023, 57: 105163. doi: 10.1016/j.istruc.2023.105163
[14] 聂春戈, 张旭, 管明珠, 等. 非承载角焊缝十字接头疲劳性能[J]. 焊接, 2021(1): 8 − 12,61. Nie Chunge, Zhang Xu, Guan Minzhu, et al. Fatigue property of non-load-carrying fillet welds in cruciform joint[J]. Welding & Joining, 2021(1): 8 − 12,61.
[15] European Committee for Standardization. Eurocode 3: design of steel structures, part 1-9: fatigue, EN 1993-1-9-2005[S]. Bruxelles: European Committee for Standardization, 2007.
[16] Hobbacher A. Recommendations for fatigue design of welded joints and components[S]. Paris: International Institute of Welding, 2008
[17] Zhao J M, Xiao L, Wei X, et al. Parametric study and neural network-based prediction for stress concentration factor of concrete-filled steel tubular T-joint[J]. Ocean Engineering, 2024, 305: 117972. doi: 10.1016/j.oceaneng.2024.117972
-
期刊类型引用(2)
1. 曲杰,王洋,王强,陈少波. 20G+316L复合钢管焊接工艺研究. 焊接技术. 2023(12): 94-99 .  百度学术
百度学术
2. 刘永滨,杜华,徐哲. 钢质燃气管道贯穿孔固相摩擦塞焊修补方法研究. 机械制造文摘(焊接分册). 2018(06): 39-43 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: