Stability of double pulse self-shielded flux-cored wire arc welding process
-
摘要:
鉴于自保护药芯焊丝在野外焊接的重要性,尤其对于野外大型机械等关键零部件的应急修复,提高其焊接成形精度至关重要,因此研究了自保护药芯焊丝在双脉冲电弧模式下的工艺稳定性. 为了实现电弧焊工艺稳定性的有效控制,采用单因素试验研究了双脉冲参数对焊接过程稳定性的影响,发现熔滴平均尺寸与电流变异系数关系密切,因此,选取强弱脉冲频率、占空比、强弱脉冲峰值和基值7个双脉冲参数作为输入值,建立一种基于RBF-BP神经网络的熔滴平均尺寸预测模型,结果表明,该预测模型有效、可行,为控制熔滴过渡过程稳定性提供了技术支撑.
-
关键词:
- 自保护药芯焊丝 /
- 工艺稳定性 /
- 熔滴过渡 /
- RBF-BP神经网络
Abstract:In view of the importance of self-protected flux-cored wire welding in the field, especially for the emergency repair of large machinery and other key parts in the field, it is very important to improve its welding forming accuracy. Therefore, the process stability of self-protected flux-cored wire in double-pulse arc mode is studied. In order to control the stability of arc welding process effectively, the influence of double pulse parameters on the stability of arc welding process was studied by single factor experiment. It was found that the average droplet size was closely related to the current variation coefficient. Based on this, 7 double pulse parameters, including strong and weak pulse frequency, duty cycle, peak current and base current of strong and weak pulses, were selected as input values, and a prediction model of the average droplet size based on RBF-BP neural network was established. The results show that the prediction model is effective and feasible, and provides technical support for controlling the stability of the droplet transition process.
-
0. 序言
自保护药芯焊丝因其良好的抗风性能和抗锈能力,以及焊接过程无需添加保护气体等优点,广泛应用于野外环境下工程机械等大型装备的焊接,其中,在野外大型机械等关键零部件的应急修复中,降低基材热输入,提高焊接成形质量具有重要意义. 在自保护药芯焊丝电弧焊中,双脉冲电弧模式具有低热输入、高熔敷效率的优点,因此选取双脉冲电弧模式研究自保护药芯焊丝电弧焊工艺的稳定性,由于自保护药芯焊丝成分复杂,有造渣、造气等成分,焊接过程中受热不均匀,造成严重飞溅,从而降低焊接过程稳定性,减小成形精度,因此研究自保护药芯焊接过程的稳定性,提高焊接质量至关重要.
国内外学者开展了大量关于药芯焊丝电弧焊工艺参数优化调节和熔滴过渡过程的研究,药芯焊丝电弧焊焊接过程中快速加热与冷却后产生角变形,角变形的幅度取决于焊接的输入参数. Aryan等人[1] 建立了数学模型来优化输入变量,使产生的角变形最小化,并利用响应曲面法(response surface methodology,RSM)检验模型的充分性并分析图形结果;在双相不锈钢熔覆过程中,Senthilkumar等人[2]研究了不同药芯焊丝电弧焊(fluxed-cored arc welding,FCAW)工艺参数对熔覆性能的影响,采用多元回归方法建立了工艺参数与熔覆性能参数特征的数学模型;Costa等人[3] 为降低水下药芯电弧焊焊接过程中ASTM A36钢板焊缝的表面孔隙率,运用向量回归(support vector regression,SVR)模型和顺序二次规划(sequential quadratic programming,SQP)方法对焊接工艺参数进行预测并设计试验,改变电压、焊接速度与进丝速度等工艺参数加以验证,结果表明,在两种数学方法的预测下可以得到比较理想的焊接工艺参数,从而得到最小表面孔隙率的水下焊缝;Qi等人[4]研究了焊接工艺条件对自保护药芯焊丝焊接高压油气输送管道环焊缝的影响,发现导致焊缝冲击韧性不合格的主要因素是焊接热输入、焊缝晶粒粗大等因素;Sartori等人[5]为提高焊缝的力学性能,研究了脉冲药芯电弧焊参数(脉冲电流和频率、焊接速度和接触尖端工作距离)与马氏体熔覆层的焊缝形貌、显微组织形成、残余应力和硬度之间的关系,结果表明,较低的热输入会导致更高的硬度,和较低的残余应力,需要适当的热输入,才能达到较好的力学性能.
熔滴过渡行为和成形过程决定堆焊的稳定性和质量,Liu等人[6]研究了自保护药芯焊丝的熔滴过渡行为以及由此产生的焊接飞溅,发现无电弧中断的液桥过渡、球状排斥过渡模式是熔滴过渡过程中的主要形式;Fu等人[7]研究了不同工艺参数下,水下药芯焊丝电弧焊时熔滴过渡方式对飞溅和电弧稳定性的影响,结果表明,局部液滴排斥飞溅的产生归因于过大且不稳定的排斥力,而液滴爆炸飞溅则是由不稳定的排斥力和气体动力引起的;Yang等人[8]建立了耦合电弧和熔滴行为的水下药芯焊丝电弧焊非轴对称三维数值模型,分析了熔滴偏离焊丝角度对焊接过程的影响,结果表明,在合力作用下熔滴偏移角度是随机的,熔滴内部流场呈现不均匀分布,导致熔滴旋转,最终影响焊缝成形;栗卓新等人[9]发现电流、电压在熔滴过渡过程中主要对熔滴所受的电弧力以熔滴过渡的形式和时间产生影响,从而影响熔滴过渡保护效果;Zhao等人 [10]利用高速相机拍摄了不同脉冲电流下的电弧和熔滴过渡图像,对图像进行了分析,发现焊丝熔化过程中的滞后熔化现象导致了渣桥过渡和液桥过渡两种接触过渡模式,熔滴的过渡方式影响电弧温度场和电弧内药芯成分的分布.
通过优化电弧焊工艺参数,控制熔滴过渡行为实现了熔滴过渡过程稳定性的控制,但是针对双脉冲自保护药芯焊丝电弧焊双脉冲参数设置较多,且受到药芯成分复杂性、焊丝结构特殊的限制,焊接过程受热不均,易发生飞溅,所以针对双脉冲自保护药芯焊丝稳定性调控的研究仍然很少,因此,文中尝试通过优化双脉冲参数,建立基于RBF-BP神经网络的熔滴平均尺寸预测模型,实现熔滴过渡过程稳定性的控制.
1. 试验方法
1.1 试验设备
图1为电弧焊试验系统,由机器人系统、焊接系统、三维扫描系统以及熔滴拍摄系统等组成. 机器人系统选用Universal-Robots公司生产的便携式小型负载的UR10焊接机器人,其工作最大有效负载为10 N,重复定位精度为0.1 mm,满足焊接机器人的适配要求. 焊接系统采用的是KEMPPI A7 MIG 焊机,焊接功率为18.4 kW,输出电流和输出电压分别为20 ~ 450 A和12 ~ 46 V. 三维扫描系统主要包括EinScan Pro 2X 三维扫描仪、点云重构软件以及图像处理软件. 熔滴拍摄系统是基于Labview软件搭建的熔滴图像、电流和电弧电压信号的同步采集平台,其程序如图2所示,该系统主要采用i-SPEED3奥林巴斯高速摄像机,以获取熔滴过渡图像,使用LHB500A5VY4型霍尔电流传感器和LHB-T1型霍尔电压传感器采集焊接电流、电弧电压信号,设置采集频率为100 kHz.
1.2 试验材料
试验选取直径为1 mm的O形钛型自保护药芯焊丝,属于E71T-GS型填充焊丝,型号为GB/T10045-2001 E500T-GS,产自捷恩特焊材(大连)有限公司,熔覆层主要的化学成分见表1,选取45号钢作为试验母材,具体尺寸为150 mm × 150 mm × 10 mm成分见表2.
表 1 熔覆层的化学成分(质量分数,%)Table 1. Chemical composition of cladding layerC Mn Si P S Al 0.12 0.51 0.22 0.008 0.007 0.93 表 2 母材的组成成分(质量分数,%)Table 2. Composition of the base metalC Mn Si S P Fe 0.42 ~ 0.50 0.50 ~ 0.80 0.17 ~ 0.37 ≤0.035 ≤0.035 余量 1.3 试验方法
经前期大量试验,双脉冲电弧模式具有高熔敷效率、低热输入、易发生熔滴过渡等优点,更适用于自保护药芯焊丝的焊接,但双脉冲参数对熔滴过渡过程的影响机制不清晰,仍需分析研究,因此,文中采用单因素变量法,研究了双脉冲电弧模式的关键参数包括强弱脉冲群的频率、峰值和基值以及占空比对熔滴过渡的影响,试验参数见表3 ~ 表5.
表 3 不同脉冲频率下的试验参数Table 3. Test parameters at different frequencies序号 强脉冲群
频率fs/Hz弱脉冲群
频率fw/Hz强脉冲群焊接电流Is/A 弱脉冲群焊接电流Iw/A 占空比
D(%)峰值 基值 峰值 基值 A1 200 100 195 40 160 35 50 A2 150 150 195 40 160 35 50 A3 100 200 195 40 160 35 50 A4 50 50 195 40 160 35 50 表 4 不同峰值和基值电流下的试验参数Table 4. Test parameters under different peak current and basical current序号 强脉冲群
频率fs/Hz弱脉冲群
频率fw/Hz强脉冲群焊接电流Is/A 弱脉冲群焊接电流Iw/A 平均焊接电流
I/A占空比
D(%)峰值 基值 峰值 基值 B1 150 150 180 35 140 28 96 50 B2 150 150 185 40 150 30 101.25 50 B3 150 150 195 45 160 35 108.75 50 B4 150 150 200 50 180 40 117.5 50 表 5 不同占空比下的试验参数Table 5. Test parameters under different duty ratios序号 强脉冲群
频率fs/Hz弱脉冲群
频率fw/Hz强脉冲群焊接电流Is/A 弱脉冲群焊接电流Iw/A 占空比
D(%)峰值 基值 峰值 基值 C1 150 150 195 40 160 35 10 C2 150 150 195 40 160 35 30 C3 150 150 195 40 160 35 60 C4 150 150 195 40 160 35 80 2. 结果与分析
2.1 脉冲频率对熔滴平均尺寸及工艺稳定性的影响
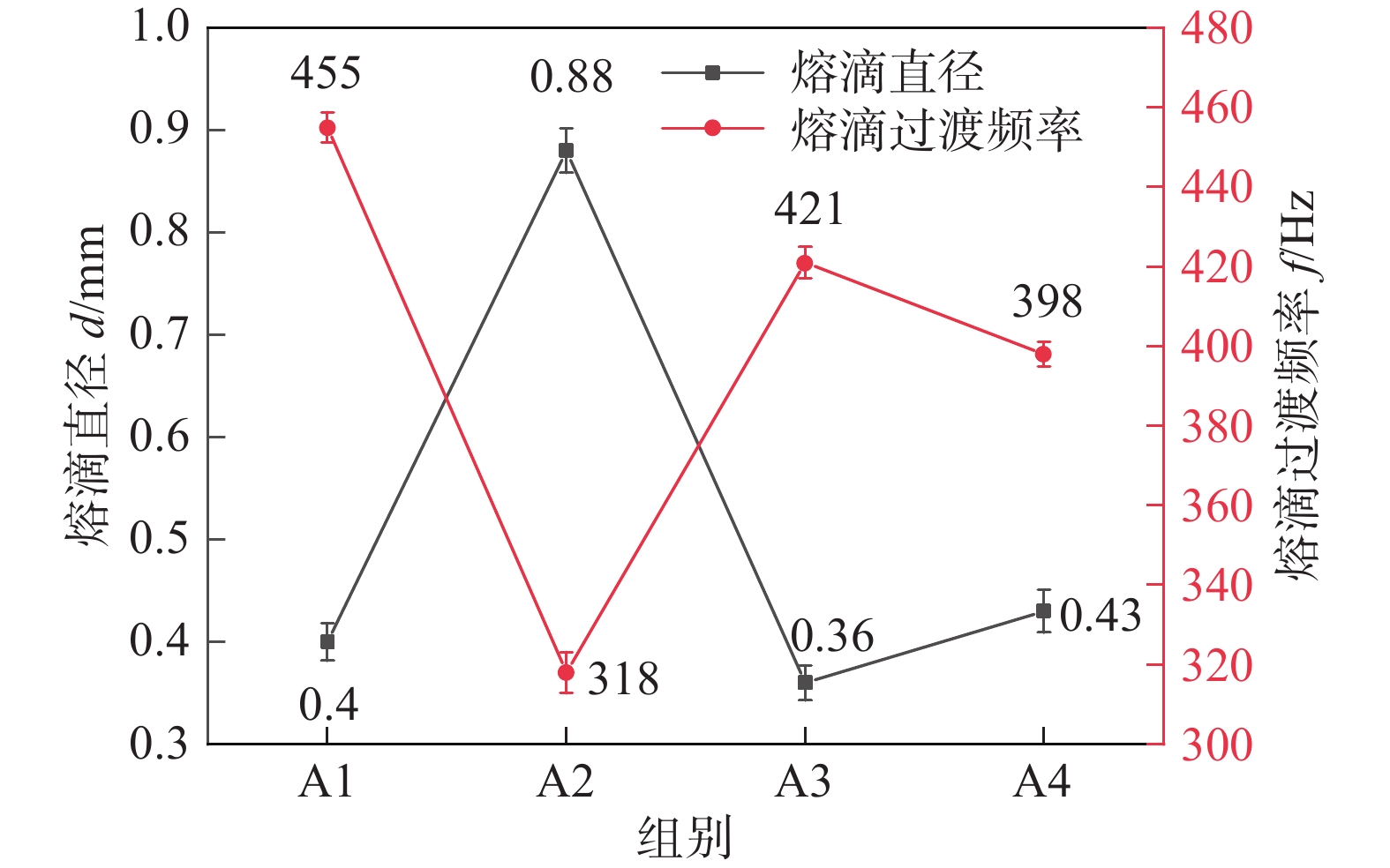
通过改变强弱脉冲群频率,得到的熔滴平均尺寸和过渡频率如图3所示,A2组的熔滴平均尺寸最大,达到了0.88 mm,过渡频率最小,仅仅只有318 Hz,此时,强弱脉冲频率皆为150 Hz,而A3组的熔滴尺寸最小,仅仅0.36 mm,其中,强脉冲频率为100 Hz,弱脉冲群频率为200 Hz,可以发现,当强弱脉冲频率不相等时,熔滴平均尺寸较小,不超过0.5 mm.
计算不同脉冲频率时的电流变异系数,即标准差与平均值之比,如图4所示. 电流变异系数最小为0.023 2,此时,强弱脉冲频率相同,电流变异系数最大可达0.076 6是前者的3倍多,另外两组的变异系数也达到了0.06以上,强弱脉冲群频率的的变化对熔滴过渡的稳定性影响较大.
2.2 脉冲峰值、基值对熔滴平均尺寸及工艺稳定性的影响
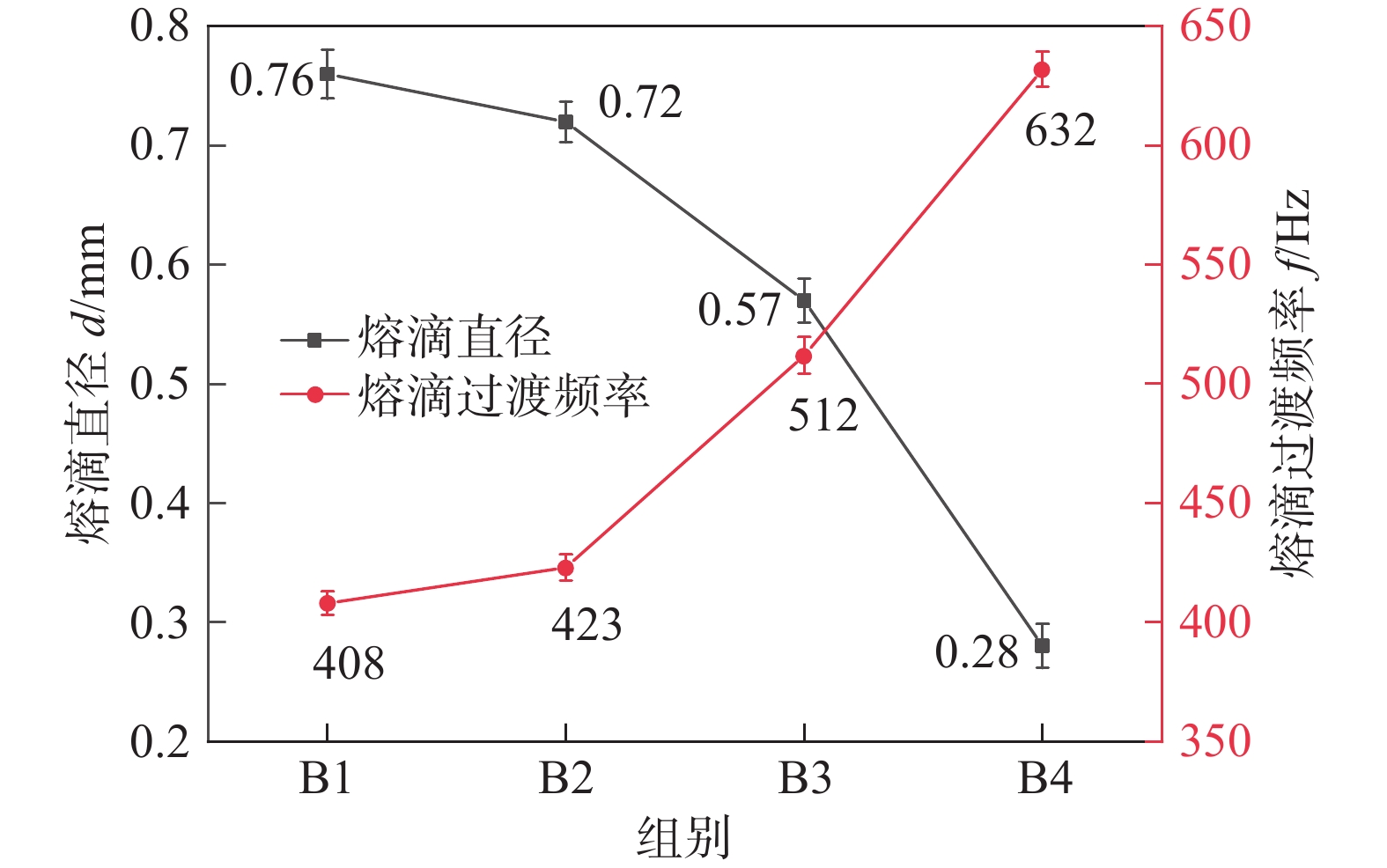
通过改变脉冲电流得到的熔滴平均尺寸和过渡频率的变化,如图5所示,随着电流平均值的增加,熔滴的平均尺寸呈下降趋势,过渡频率呈上升趋势,熔滴尺寸最小值为0.28 mm,此时,平均脉冲电流最大,并且熔滴过渡频率也达到最大.
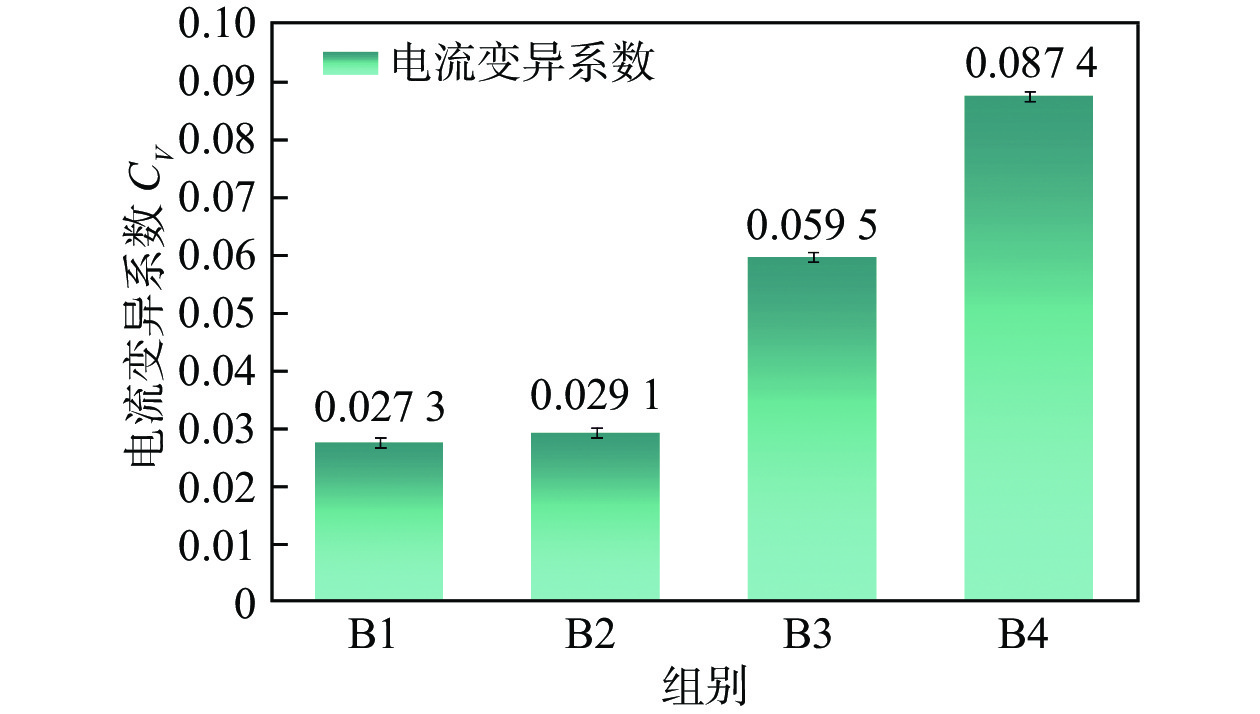
计算不同脉冲电流时的电流变异系数,如图6所示,随着平均电流的增大,电流变异系数逐渐增大,最大电流变异系数是最小值的3.2倍,由此可见,脉冲电流是影响焊接工艺稳定性的因素之一.
2.3 占空比对熔滴平均尺寸及工艺稳定性的影响
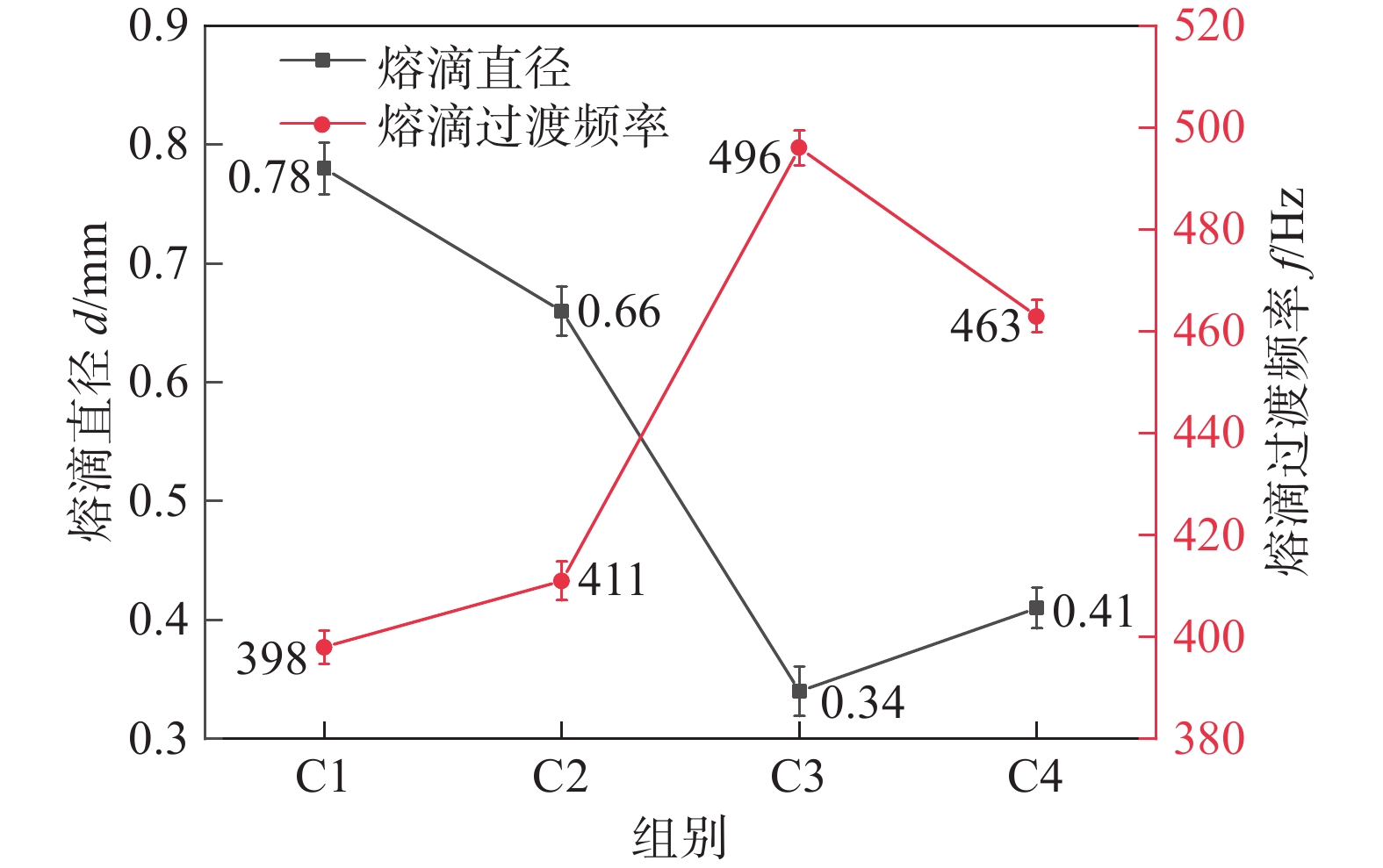
通过改变占空比,得到的熔滴平均尺寸和过渡频率的变化,如图7所示,从图中可以看出,占空比的增大会导致熔滴尺寸先减小后增大,而过渡频率先增大后减小,当占空比为10%时,熔滴的平均尺寸最大,过渡频率最小,相反,当占空比为60%时,熔滴的尺寸最小,过渡频率最大.
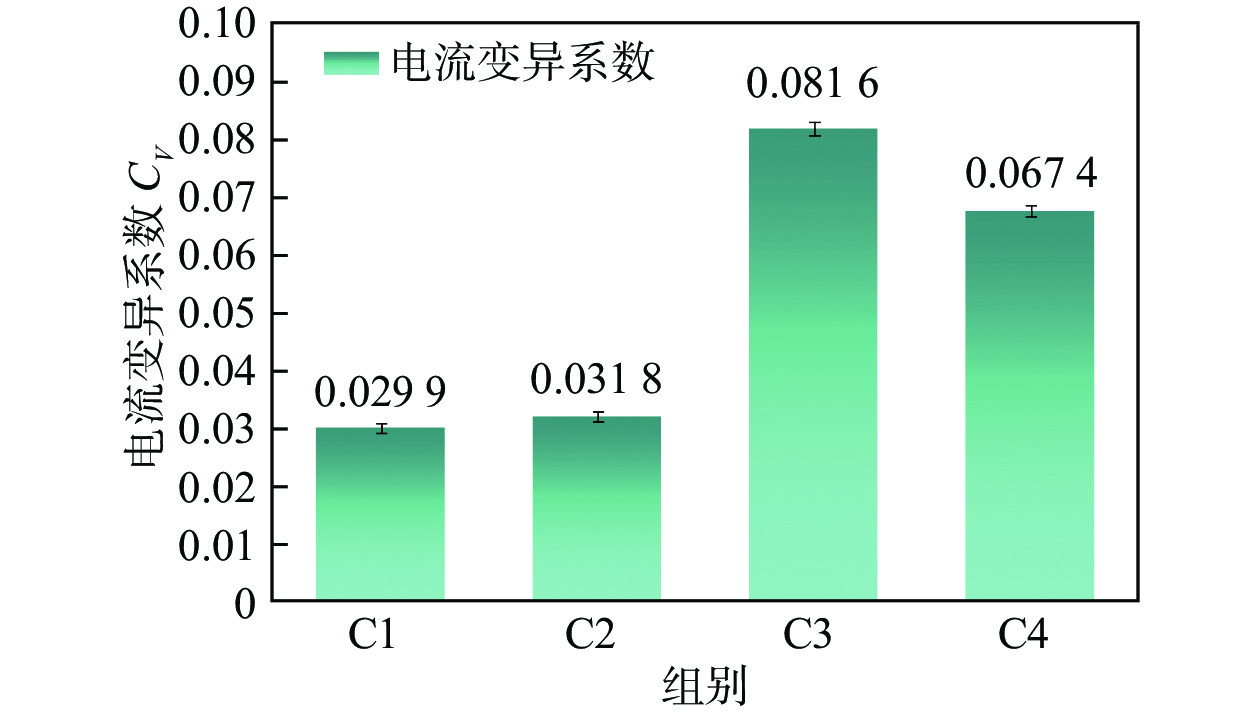
计算不同占空比下的电流变异系数,如图8所示,随着占空比的增大,电流变异系数呈现先上升后下降的趋势,占空比低于60%时,电流变异系数较小,占空比为60%时,C3组的电流变异系数相比于C2组增大了2.5倍,由此说明,占空比也是焊接工艺稳定性的影响因素之一.
2.4 熔滴平均尺寸对工艺稳定性的影响
由于试验设计的脉冲参数之间存在“强耦合”关系,对熔滴尺寸、熔滴过渡频率和电流变异系数的影响规律并不明显,所以难以通过少数几个参数的优化实现对熔滴过渡过程的控制,但通过计算不同熔滴尺寸下的变异系数,得到熔滴尺寸与电流变异系数的变化,如图9所示,发现熔滴尺寸与电流变异系数存在内在联系,同时对数据点进行多项式拟合得到式(1),结果表明,电流变异系数随着熔滴尺寸的增大而逐渐减小,焊接工艺稳定性随之升高,这为进一步控制熔滴过渡过程提供了参考.
$$ CV = 0.141 - 0.209d - 0.082{d^2} $$ (1) 式中:CV表示电流变异系数;d表示熔滴直径.
2.5 熔滴平均尺寸预测模型的建立
为了提高焊接修复过程的工艺稳定性,基于熔滴尺寸和电流变异系数的关系,建立了一种以双隐层组合神经网络—径向基神经网络(radial basis function, RBF)和反向传播神经网络(back propagation, BP)为基础的熔滴平均尺寸预测模型,可为双脉冲参数的设置提供参考,实现对熔滴过渡过程的控制,使其表现为大尺寸一脉一滴过渡模式.
2.5.1 RBF-BP神经网络的基本原理
RBF-BP神经网络模型结合了BP神经网络强大的自学能力、较强的泛化能力和RBF神经网络收敛速度快、无局部极小值存在的优点,提高了神经网络的预测精度,该模型采用7输入1输出的模式,脉冲参数作为输入值,熔滴尺寸作为输出值,模型包含一个输入层、两个隐含层和一个输出层,双隐含层由RBF隐含层和BP隐含层组成,其中的传递函数分别为高斯函数和Sigmoid函数,预测模型结构示意图如图10所示.
2.5.2 RBF-BP神经网络的设计
选取影响熔滴尺寸的强弱脉冲频率、强弱脉冲群峰值、基值以及占空比这7个双脉冲参数作为神经网络的输入值,熔滴平均尺寸作为输出值. 选用前期试验的50组数据作为样本,10组数据作为验证,采用Kolmogorov定理确定隐含层神经元节点数,如式(2) ~ 式(3)所示
$$ M < 2n + 1 $$ (2) $$ M = \sqrt {n + m} + a $$ (3) 式中:M为隐含层的神经元数目;n为输入层节点数;m为输出层节点数;a取1 ~ 10的常数,经过比较发现,当M=8时,优化速度最快,收敛最好.
RBF-BP神经网络的实现步骤如下.
(1)随机赋予网络初始权值wij和阀值θj,设置最大迭代次数和目标误差值,设置网络误差平方和的初始值为0.
(2)输入样本数据,设置RBF网络隐含层的传递函数为高斯函数
$$ s({j})=\exp \left[\sum_{j=1}^{N_1}{\dfrac{\left|x_i-w_{1, j}\right|} { 2 \sigma_j^2}}\right] $$ (4) 式中:j是隐含层的节点数,j=1,2,···,n;s是第j个隐含层节点的输出量;xi是输入变量,i=1,2,···,K;w1,j为第j个RBF隐含层节点的权值向量;
$\sigma_j^2 $ 是第j个节点的高斯核函数宽度;N1为RBF隐含层的节点数.(3) 将RBF网络的输出值作为BP网络的输入值,BP网络隐含层的传递函数为Sigmoid函数
$$ F(y)=\frac{1}{1+\mathrm{e}^{-y}} $$ (5) 输出函数为
$$Y({t})=F\left[\sum_{j=1}^{N_2} w_{2, {t}} s(j)\right] $$ (6) 式中:t为BP隐含层节点数,t=1,2,…,N2;w2,t为第j个RBF隐含层节点与第t个BP隐含层节点的权值;N2为BP隐含层节点数.
(4)计算第m个节点的输出值
$$ Y({m})=F\left[\sum_{t=1}^{N_3} w_{3, {m}} Y(t)\right]$$ (7) 式中:w3,m为第t个BP隐含层节点与第m个输出层节点之间的权值;N3为输出层的节点数目.
(5)计算误差平方和
$$E=\sum_{t=1}^{N_3}\left[c_t-Y(m)\right]^2 $$ (9) 式中:ct为实际输出值.
(6)调整权值和阀值.
(7)设置的目标误差大于实际训练误差时,整个过程收敛,该网络训练结束.
2.5.3 训练结果与讨论
试验网络训练函数设置为Traindm函数,最大训练次数设置为180次,训练步长为10,学习率为0.02,期望误差为10−5,通过80组样本数量的训练得到预测值,预测结果见表6,选取表3 ~ 表5的数据作为验证数据,对比结果如图11所示,由表6可知,最大相对误差为12.19%,最小为1.51%,根据预测值和真实值的对比示意图可知,预测值与真实值基本吻合,说明该模型能准确预测熔滴的平均尺寸,可以为双脉冲参数设置提供参考,实现对熔滴平均尺寸的控制,提高焊接过程稳定性.
表 6 熔滴直径的预测结果Table 6. Prediction of droplet diameter序号 预测值d1/mm 实际值d2/mm 相对误差E(%) A1 0.38 0.40 9.52 A2 0.82 0.88 6.81 A3 0.33 0.36 8.33 A4 0.46 0.43 6.97 B1 0.78 0.76 2.63 B2 0.70 0.72 2.77 B3 0.58 0.57 1.75 B4 0.25 0.28 10.71 C1 0.73 0.78 6.41 C2 0.65 0.66 1.51 C3 0.32 0.34 5.88 C4 0.46 0.41 12.19 3. 结论
(1)熔滴平均尺寸与电流变异系数密切相关,熔滴尺寸在0.6 ~ 0.9 mm时,焊接电流变异系数小于0.04,熔滴过渡的稳定性较好.
(2)占空比的增大会导致熔滴尺寸先减小后增大,而过渡频率先增大后减小,占空比低于60%时,焊接电流变异系数较小,高于60%时,电流变异系数增大了一倍.
(3)建立一种基于RBF-BP组合神经网络的熔滴平均尺寸预测模型,结果表明,该模型预测结果令人满意,能有效预测熔滴直径,为双脉冲参数的设置提供了参考,进一步提高了焊接过程稳定性和焊接质量.
-
表 1 熔覆层的化学成分(质量分数,%)
Table 1 Chemical composition of cladding layer
C Mn Si P S Al 0.12 0.51 0.22 0.008 0.007 0.93 表 2 母材的组成成分(质量分数,%)
Table 2 Composition of the base metal
C Mn Si S P Fe 0.42 ~ 0.50 0.50 ~ 0.80 0.17 ~ 0.37 ≤0.035 ≤0.035 余量 表 3 不同脉冲频率下的试验参数
Table 3 Test parameters at different frequencies
序号 强脉冲群
频率fs/Hz弱脉冲群
频率fw/Hz强脉冲群焊接电流Is/A 弱脉冲群焊接电流Iw/A 占空比
D(%)峰值 基值 峰值 基值 A1 200 100 195 40 160 35 50 A2 150 150 195 40 160 35 50 A3 100 200 195 40 160 35 50 A4 50 50 195 40 160 35 50 表 4 不同峰值和基值电流下的试验参数
Table 4 Test parameters under different peak current and basical current
序号 强脉冲群
频率fs/Hz弱脉冲群
频率fw/Hz强脉冲群焊接电流Is/A 弱脉冲群焊接电流Iw/A 平均焊接电流
I/A占空比
D(%)峰值 基值 峰值 基值 B1 150 150 180 35 140 28 96 50 B2 150 150 185 40 150 30 101.25 50 B3 150 150 195 45 160 35 108.75 50 B4 150 150 200 50 180 40 117.5 50 表 5 不同占空比下的试验参数
Table 5 Test parameters under different duty ratios
序号 强脉冲群
频率fs/Hz弱脉冲群
频率fw/Hz强脉冲群焊接电流Is/A 弱脉冲群焊接电流Iw/A 占空比
D(%)峰值 基值 峰值 基值 C1 150 150 195 40 160 35 10 C2 150 150 195 40 160 35 30 C3 150 150 195 40 160 35 60 C4 150 150 195 40 160 35 80 表 6 熔滴直径的预测结果
Table 6 Prediction of droplet diameter
序号 预测值d1/mm 实际值d2/mm 相对误差E(%) A1 0.38 0.40 9.52 A2 0.82 0.88 6.81 A3 0.33 0.36 8.33 A4 0.46 0.43 6.97 B1 0.78 0.76 2.63 B2 0.70 0.72 2.77 B3 0.58 0.57 1.75 B4 0.25 0.28 10.71 C1 0.73 0.78 6.41 C2 0.65 0.66 1.51 C3 0.32 0.34 5.88 C4 0.46 0.41 12.19 -
[1] Aryan A, Drishti A, Pradeep K. Development of a mathematical model to predict angular distortion in FCA welded stainless steel 301 plates[J]. Materials Today:Proceedings, 2023, 78(P3): 608 − 613.
[2] Senthilkumar B, Kannan T, Madesh R. Optimization of flux-cored arc welding process parameters by using genetic algorithm[J]. The International Journal of Advanced Manufacturing Technology, 2015, 93(1-4): 35 − 41.
[3] Costa Patricia S, Altamirano Guerrero Gerardo, Ochoa Palacios Rocio M, et al. Optimization of welding parameters in underwater wet FCAW on a structural steel using support vector regression and sequential quadratic programming[J]. The International Journal of Advanced Manufacturing Technology, 2022, 121(5-6): 4225 − 4236. doi: 10.1007/s00170-022-09584-4
[4] Qi L H, Jin Z L, Zhang J M, et al. Influence factors of X80 pipeline steel girth welding with self-shielded flux-cored wire[J]. Materials Science and Technology, 2016, 33(5): 592 − 601.
[5] Sartori J M, Faria F C, Alves C C, et al. Pulsed FCAW of martensitic stainless clads onto mild steel: microstructure, hardness, and residual stresses[J]. Materials, 2022, 15(8): 2715 − 2715. doi: 10.3390/ma15082715
[6] Liu H Y, Li Z X, Li H, et al. Study on metal transfer modes and welding spatter characteristics of self-shielded flux cored wire[J]. Science and Technology of Welding and Joining, 2008, 13(8): 777 − 780. doi: 10.1179/174329308X380354
[7] Fu Yunlong, Guo Ning, Du Yongpeng, et al. Effect of metal transfer mode on spatter and arc stability in underwater flux-cored wire wet welding[J]. Journal of Manufacturing Processes, 2018, 35: 161 − 168. doi: 10.1016/j.jmapro.2018.07.027
[8] Yang Jie, Xu Shichang, Jia Chuanbao, et al. Numerical analysis of arc parameters and droplet behaviors for underwater flux-cored arc welding[J]. International Journal of Thermal Sciences, 2023, 194, 108601.
[9] 栗卓新, 皇甫平, 陈邦固. 自保护药芯焊丝熔滴过渡的控制[J]. 机械工程学报, 2001, 37(7): 108 − 112. Li Zhuoxin, Huang Fuping, Chen Banggu. Control of droplet transition of self-protecting flux-cored wire[J]. Journal of Mechanical Engineering, 2001, 37(7): 108 − 112.
[10] Zhao Xiaoyan, Yang Lijun, Huang Yiming, et al. Study on arc characteristic of flux-cored wire pulse TIG arc additive manufacturing[J]. Spectroscopy and Spectral Analysis, 2021, 41(8): 2397 − 2403.




 下载:
下载: