Recognition algorithm of small-diameter tube X-ray welding defect image
-
摘要:
针对小径管X射线焊缝图像缺陷检测精确率低的现状，通过对图像进行特征分析并结合稀疏字典学习，提出一种基于图像分割的小径管焊缝图像缺陷检测算法. 首先，对小径管焊缝图像进行两步图像分割获得感兴趣区域；其次，提取焊缝缺陷，得到缺陷疑似局部图像；最后，提出以不同类型原子间相关性最小为目标的小径管焊缝缺陷字典矩阵数学模型并使用K-SVD算法进行求解，利用该字典矩阵实现圆形缺陷、线形缺陷和噪声的分类鉴别. 为提高系统实时性，使用并行编程对图像分割算法进行加速. 结果表明，改进后缺陷字典矩阵对圆形缺陷识别成功率为0.974，线形缺陷识别成功率为0.967，且具有较快的识别速度，实现了小径管焊缝图像缺陷的有效识别.
Abstract:To address the current situation of low accuracy rate of small-diameter tube welding image defect detection, by combining image feature analysis and sparse dictionary learning, a small-diameter tube welding defect detection algorithm based on image segmentation is proposed. Firstly, using two-step image segmentation way acquires the region of interest which is in small-diameter tube welding image. Secondly, the suspected defect region is obtained by extracting welding defect. Finally, we propose a mathematical model of the dictionary matrix of small-diameter tube welding defects with the objective of minimizing correlations between different types of atoms and solve it by using K-SVD algorithm. After that, the dictionary matrix is used to classify circular defects, strip defects and noise. To improve the real-time performance of the system, we use parallel programming to accelerate the image segmentation algorithm. The results show that the recognition rate of the proposed method is 0.974 for circular defects and 0.967 for strip defects, and the recognition speed is fast, which enables the effective recognition of defects in small-diameter tube welding image.
-
0. 序言
小径管结构在油气地面装置中的应用十分广泛. 在焊接过程中，受外部环境和焊接条件的影响，其焊缝区域不可避免的产生诸如：气孔，裂纹，夹渣和焊瘤等缺陷[1]. 这些缺陷不仅影响工件的外观，还会影响工件的结构强度和性能. 更严重的是，缺陷会对工件使用者造成一些潜在的安全隐患[2-4]. 因此，焊缝质量检测是焊接过程结束后的一道关键环节. 无损检测技术可以在不影响被检测对象性能的基础上探测物体在制造与使用过程中的缺陷问题[5-6]. 在施工现场的检测流程中，主要采用无损检测方式作为焊缝缺陷的检测方法.
小径管焊缝缺陷的无损检测方法主要包括超声检测和射线检测. 其中，超声相控阵检测技术可以检测缺陷的高度和埋深，且具有高精度和环保的特点，成为当前小径管缺陷检测领域的研究热点. 基于超声检测的方法，江野等人[7]将超声相控阵检测技术应用于奥氏体异种钢薄壁小口径管道对接焊缝的裂纹检测. 陈小明等人[8]探究了将超声相控阵检测技术应用于蛇形管高压加热器超小径管焊缝检测的可行性.
近年来，伴随射线检测技术逐渐成熟，部分学者也试想将射线检测技术应用于小径管焊缝缺陷检测中. Xie等人[9]将超声相控阵检测和射线检测对小径管焊缝缺陷的检测效果进行对比，结果表明射线检测对体积型缺陷的检测更为精准，检测结果更直观且可永久保存. 贾潇等人[10]的研究也表明在对缺陷类型的判别上，射线检测更具有优势. 然而，目前未见基于射线检测技术实现小径管焊缝缺陷检测的相关算法和文献.
综上所述，该文从射线检测的角度出发，针对小径管结构，通过两步分割获取感兴趣区域(the region of interest，ROI)，提取缺陷疑似局部图像(suspected defect region，SDR)，构造字典矩阵数学模型并分析了字典矩阵原子数对识别精度的影响，最终确定了具体的原子数，使用字典矩阵对数据库中的图像进行检测，验证了所提方法的可行性，在验证过程结束后，对部分缺陷识别错误的原因进行可能性分析.
1. 试验方法
1.1 图像分析
实际工业生产中，小径管的X射线检测图像如图1所示，图1(b)为小径管在双壁双影椭圆透照下的图像，图1(c)为小径管在双臂双影垂直透照下的图像. 垂直透照下，小径管焊缝图像对于面积型缺陷的检出率较高，且面积型缺陷如裂纹等对焊管的危害性相比于气孔等缺陷更大，故选取垂直透照下的小径管图像作为研究对象.
![]()
图 1 小径管X射线图像Figure 1. X-ray image of small diameter tube. (a) original image; (b) elliptical image with tilt radiography; (c) overlapping image with vertical radiography由图1可知，射线图像包含背景区域和小径管区域，缺陷存在于小径管中的焊缝区域. 由于焊缝图像在采集时会受到光照和表面反射的影响，所以背景存在一些较暗的阴影区域[11]，阴影区域像素值范围与小径管区域相差较大，可以通过图像分割的方式提取小径管区域. 部分小径管射线图像表现为低对比度，分割时要求算法具有较强的鲁棒性，且实际的小径管射线图像都具有高噪声的特点，分割算法应具有良好的降噪效果.
1.2 ROI提取
X射线焊缝图像背景起伏，背景区域的存在既降低算法的运行速度，又对缺陷识别产生干扰. 因此，提取ROI区域是进一步实现缺陷识别的重要中间环节. 从原始图像可知，焊缝区域处于小径管区域内，难以通过分割算法直接提取焊缝区域. 故采用两步分割的方法，即先提取小径管区域，再从小径管区域图像中提取焊缝区域. 具体的图像分割算法流程如下.
1.2.1 小径管区域提取
(1) 图像增强与降噪：利用Gamma变换增强小径管X射线图像
${\text{S}}$ 得到图像${{\text{S}}_1}$ ，使用中值滤波和均值滤波算法对图像${{\text{S}}_1}$ 进行降噪处理得到图像${{\text{S}}_2}$ .(2) 二值化：使用Ostu分割
${{\text{S}}_2}$ 得到二值图像${{\text{B}}_1}$ .(3) 获取小径管区域连通域：使用种子填充法提取
${{\text{B}}_1}$ 中所有连通域区域，并用模板匹配算法对每个连通域进行处理，含有模板${\text{T}}$ 的连通域即为小径管区域${\text{L}}$ .(4) 获取小径管区域图像：利用小径管区域连通域
${\text{L}}$ 的外接矩形获得对应原图${{\text{S}}_2}$ 的小径管区域，记为${{\text{M}}_1}$ .1.2.2 焊缝区域提取
(1) 二值化：使用Ostu分割图像
${{\text{M}}_1}$ 得到二值图像${{\rm{B}}_2}$ .(2) 获取最大连通域：使用种子填充法提取图像
${{\text{B}}_2}$ 连通域，对比连通域面积，将小于最大面积的连通域设定为背景区域，处理后的图像记为${{\text{B}}_3}$ .(3) 统计图像
${{\text{B}}_3}$ 每列像素的平均值，若平均值超过一定阈值，记此列为焊缝子列，所有焊缝子列的组合区域即为感兴趣焊缝区域ROI.为验证小径管焊缝分割算法的合理性，使用某石油公司提供的焊接数据库对小径管X射线图像进行ROI提取试验. 数据库中共有3535张现场实拍图像，通过上述方法对3535张图像进行分割试验，结果表明有3487张图像可以准确提取ROI，有效分割率为98.6%，剩余48张图像识别错误经检查原因为质量很差不具有分割意义或中心标记与管道边缘严重重合. 分割试验过程中，所提方法表现出良好的鲁棒性，对对接接头焊口图像和马鞍形焊口图像的ROI分割都表现出良好的效果分别如图2和图3所示.
![]()
图 2 ROI区域提取算例1Figure 2. ROI extraction example 1. (a) original image; (b) segmented image![]()
图 3 ROI区域提取算例2Figure 3. ROI extraction example 2. (a) original image; (b) segmented image分割过程中，即使部分图像质量较差或者图像中管道区域有弯曲如图4和图5所示，分割算法也可以准确分割.
![]()
图 4 ROI区域提取算例3Figure 4. ROI extraction example 3. (a) original image; (b) segmented image![]()
图 5 ROI区域提取算例4Figure 5. ROI extraction example 4. (a) original image; (b) segmented image1.3 字典矩阵模型及求解
小径管焊缝区域内缺陷类型较多，不同类型的缺陷具有不同的特征，对焊管的危害性也不同. 因此，在缺陷的识别过程中，不仅要确定是否为缺陷，还要精准判定缺陷的类型. 圆形缺陷和线形缺陷是小径管焊缝区域内最为常见和危害性较大的两类缺陷，噪声是缺陷识别过程中的干扰因素，将三者作为识别对象可有效覆盖大部分缺陷类型. 利用文献[12]中的灰度密度聚类算法可获得焊缝区域内圆形缺陷，线形缺陷和噪声所对应的SDR图像. 图6为SDR示意图，图中的外切矩形区域为疑似缺陷的外切矩形，扩展5个像素点后的区域为SDR. 按其方法提取出的部分SDR如图7所示. SDR面积较小，传统基于特征提取的方法难以获得图像的显著特征，识别过程中容易误判一些细小缺陷. 稀疏字典学习可通过稀疏系数直接识别SDR类型，避免了特征提取过程，在小径管焊缝缺陷识别过程中具有独特优势.
![]()
图 7 疑似局部图像事例Figure 7. Example of suspected defect region. (a) SDR of round defects; (b) SDR of linear defects; (c) SDR of noise稀疏字典学习是从庞大数量的样本中找出最具代表性的原子组成字典，并用字典中的原子对样本进行稀疏描述[13]. 设
${\boldsymbol{y}}$ 为待检测样本，稀疏字典学习的表达式为$$ {\boldsymbol{y}} = {d_1}{x_1} + {d_2}{x_2} + \cdots + {d_n}{x_n} = {\boldsymbol{DX}} $$ (1) 式中：
${\boldsymbol{D}} {\text{ = }} [{d_1},{d_2}, \cdots ,{d_k}] \in {R^{m \times k}}$ ，表示字典矩阵中的原子数为$k$ ；${\boldsymbol{X}} = [{x_1},{x_2}, \cdots ,{x_i},0,0, \cdots ]\in {R^{k \times n}}$ ，表示待检测样本${\boldsymbol{y}}$ 可由$n$ 个$k$ 维列向量线性表示.小径管焊缝缺陷字典矩阵中，原子是由SDR的像素点按照列优先的原则逐列排列而成，表示为
$$ \begin{split} {\boldsymbol{D}} = &\{ {d_1},{d_2}, \cdots ,{d_{{C_{{d}}}}}, {d_{{C_{{d}}} + 1}},{d_{{C_{{d}}} + 2}}, \cdots ,{d_{{C_{{d}}} + {L_{{d}}}}},{d_{{C_{{d}}} + {L_{{d}}} + 1}} ,\\&{d_{{C_{{d}}} + {L_{{d}}} + 2}}, \cdots ,{d_{{C_{{d}}} + {L_{{d}}} + {N_{{d}}}}}\} \end{split} $$ (2) 式中：
${C_{{d}}}$ 表示圆形缺陷原子数；${L_{{d}}}$ 表示线形缺陷原子数；${N_{{d}}}$ 表示噪声原子数. 稀疏系数${\boldsymbol{X}}$ 中的非0系数与待检测图像类别有关，与类别无关的系数表示为0. 对${\boldsymbol{X}}$ 的求解可等效为求2范数最小化问题，即$$ {\boldsymbol{\hat X}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{ = }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{arg}}{\kern 1pt} {\text{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{X}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} |{|_{{\kern 1pt} {\kern 1pt} {\kern 1pt} 2}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{s}}{\text{.}}\;{\text{t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{y}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{ = }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{DX}} $$ (3) 式(3)可等效为
$$ {\boldsymbol{\hat X}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{ = }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \min {\kern 1pt} {\kern 1pt} {\kern 1pt} ||{\boldsymbol{y}} - {\boldsymbol{DX}}{\kern 1pt} {\kern 1pt} {\kern 1pt} |{|_{{\kern 1pt} {\kern 1pt} {\kern 1pt} 2}} $$ (4) 可使用正交匹配追踪(orthogonal matching pursuit，OMP)算法求解式(4)，得到矩阵
${\boldsymbol{X}}$ 的1个广义解.1.3.1 构建字典矩阵模型
在小径管焊缝缺陷识别过程中，可通过学习的方式获得字典矩阵
${\boldsymbol{D}}$ ，学习过程等效为求解下式$$ \begin{split} & \mathop {\min }\limits_{D,{\kern 1pt} {\kern 1pt} X} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{Y}} - {\boldsymbol{DX}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||{\kern 1pt} {\kern 1pt} _{\rm{F}}^2 \\& {\text{s}}{\text{.}}\; {\text{t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall i ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||{\kern 1pt} {\kern 1pt} {x_i}{\kern 1pt} {\kern 1pt} ||{\kern 1pt} {{\kern 1pt} _0} \leqslant \varepsilon \end{split}$$ (5) 式中：
${\boldsymbol{Y}}$ 为训练样本矩阵；$\varepsilon $ 为矩阵${\boldsymbol{X}}$ 的稀疏性.小径管X射线焊缝图像SDR可分为圆形SDR，线形SDR和噪声SDR共3类. 相同类型SDR具有一定的相似性，不同类型SDR表现出不同的特征，可以认为特定种类的SDR可由特定字典进行稀疏描述. 因此，只需分别构建3种SDR的特定字典并进行组合，即可实现字典矩阵
${\boldsymbol{D}}$ 的构建，${\boldsymbol{D}}$ 的形式如式(2)所示. 若类别数为$C$ ，可通过式(6)求解特定种类SDR对应的字典矩阵${{\boldsymbol{D}}_K}$ .$$ \begin{split} & \mathop {\arg \min }\limits_{{D_K},{X_K}} ||{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\boldsymbol{Y}}_K} - {{\boldsymbol{D}}_K}{{\boldsymbol{X}}_K}{\kern 1pt} {\kern 1pt} {\kern 1pt} ||{\kern 1pt} {\kern 1pt} _2^2 \\& {\text{s}}{\text{.}}\; {\text{t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ||x_i^K||{\kern 1pt} {{\kern 1pt} _0} \leqslant \varepsilon ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K = 1,2, \cdots ,C \end{split}$$ (6) 式中：
${{\boldsymbol{Y}}_K}$ 为第$K$ 类训练样本；${{\boldsymbol{X}}_K}$ 为第$K$ 类的稀疏系数. 字典矩阵${\boldsymbol{D}}$ 可表示为$$ {\boldsymbol{D}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{ = }}{\kern 1pt} {\kern 1pt} {\kern 1pt} [{D_1},{D_2}, \cdots ,{D_K}] $$ (7) 式(6)虽可求解矩阵
${{\boldsymbol{D}}_K}$ ，但并未对${{\boldsymbol{D}}_K}$ 中的原子数进行限制. 实际构成${\boldsymbol{D}}$ 时，训练样本可能较多，此时$k$ 值较大，较大的$k$ 值虽有利于对更加多元化的数据进行表示，但也会增加不同缺陷类型原子间的相关性. 若${\boldsymbol{D}}$ 中的原子完全正交，则仅需少量原子就可覆盖缺陷的全部特征，极大地减少可行解的数量. 鉴于此，该文从小径管X射线焊缝图像缺陷识别的唯一性和实时性角度出发，提出一种以不同类型缺陷原子相关性最小为目标的小径管焊缝缺陷字典矩阵学习模型，即$$\begin{split} & \mathop {\min }\limits_{{\boldsymbol{D}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \subset {\kern 1pt} {\kern 1pt} \varTheta } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\kern 1pt} {\kern 1pt} {\kern 1pt} ||{\boldsymbol{Y}} - {\boldsymbol{DX}}{\kern 1pt} {\kern 1pt} ||{\kern 1pt} {\kern 1pt} _F^2{\kern 1pt} {\kern 1pt} + \sum {{d_{{P_i}}}} {d_{{P_j}}}{\kern 1pt} {\kern 1pt} {\kern 1pt}\right \} \\& {\text{s}}{\text{.}}\; {\text{t}}{\text{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall q{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{||}} {x_q}{\text{||}} \leqslant \varepsilon \end{split} $$ (8) 式中：
$\varTheta$ 为所有样本的集合，$P\in \text{\{圆形}\text{SDR}，线$ 形SDR，噪声SDR$ {\text{\} }} $ ，其中${P_i}$ 表示对应类型原子区域的第$i$ 列元素，如当$P$ 为圆形SDR原子时，${P_i}$ 表示圆形SDR原子区域的第$i$ 列元素，其余变量与式(6)相同.式(8)中，字典矩阵
${\boldsymbol{D}}$ 和稀疏编码矩阵${\boldsymbol{X}}$ 均为未知量，可以使用K均值奇异值分解(K-SVD)算法，先确定${\boldsymbol{D}}$ 后计算${\boldsymbol{X}}$ ，再固定${\boldsymbol{X}}$ 更新${\boldsymbol{D}}$ 的方式交替更新求解.1.3.2 字典矩阵求解
利用K-SVD算法求解字典矩阵的算法流程如图8所示，算法运行前需预先设定字典矩阵的原子个数
$k$ . 图8中，$\min k$ 取值为20，$\max k$ 取值为80. 若$k$ 值过小则无法完整描述SDR的特征，$k$ 值过大则使类间相似性原子增多，字典冗余性增大. 再考虑到要将3种缺陷类型的字典矩阵通过式(7)进行组合，故将各缺陷类型字典矩阵原子数的最大值设为80.确定3种缺陷的字典后，按照圆形缺陷、线形缺陷、噪声的顺序将原子进行排序，记录此时字典矩阵中圆形缺陷原子数
${C_{{d}}}$ ，线形缺陷原子数${L_{{d}}}$ 和噪声原子数${N_{{d}}}$ . 对任意测试样本${\boldsymbol{y}}$ ，在${\boldsymbol{D}}$ 确定后可根据式(1)求解稀疏系数${\boldsymbol{X}}$ ，根据${\boldsymbol{X}}$ 中非0系数的分布可以判定测试样本的缺陷类型，判别方法如式(9)、式(10)和式(11)所示. 若满足式(9)判定为圆形缺陷，满足式(10)判定为线形缺陷，满足式(11)判定为噪声.$$ {\text{if}}\left\{ \left(\sum\limits_{i = 1}^{{C_{{d}}}} {{x_i}} > \sum\limits_{i = {C_{{d}}} + 1}^{{C_{{d}}} + {L_{{d}}}} {{x_i}} \right)\& \left(\sum\limits_{i = 1}^{{C_d}} {{x_i}} > \sum\limits_{i = {C_{{d}}} + {N_{{d}}} + 1}^{{C_{{d}}} + {L_{{d}}} + {N_{{d}}}} {{x_i}} \right)\right\} $$ (9) $$ {\text{if }}\left\{\left(\sum\limits_{i = {C_{{d}}} + 1}^{{C_{{d}}} + {L_{{d}}}} {{x_i}} \geqslant \sum\limits_{i = 1}^{{C_{{d}}}} {{x_i}} \right)\& \left(\sum\limits_{i = {C_{{d}}} + 1}^{{C_{{d}}} + {L_{{d}}}} {{x_i}} \geqslant \sum\limits_{i = {C_{{d}}} + {N_{{d}}} + 1}^{{C_{{d}}} + {L_{{d}}} + {N_{{d}}}} {{x_i}} \right)\right\} $$ (10) $$ {\text{if}}\left\{\left(\sum\limits_{i = {C_{{d}}} + {N_{{d}}} + 1}^{{C_{{d}}} + {L_{{d}}} + {N_{{d}}}} {{x_i}} > \sum\limits_{i{{ = 1}}}^{{{{C}}_{{d}}}} {{{{x}}_{{i}}}} \right)\&\left( \sum\limits_{i = {C_{{d}}} + {N_{{d}}} + 1}^{{C_{{d}}} + {L_{{d}}} + {N_{{d}}}} {{x_i}} > \sum\limits_{i = {C_{{d}}} + 1}^{{C_{{d}}} + {L_{{d}}}} {{x_i}} \right )\right\} $$ (11) 学习过程中，可能会出现因训练样本不同导致3种缺陷字典中的原子数互不相同的情况. 为探究这种因素的影响，设计了1个
$k$ 值为80的字典，字典中圆形缺陷SDR设定为50，线形缺陷SDR设定为25，噪声SDR设定为5，利用此字典进行识别试验. 结果表明，${\boldsymbol{X}}$ 中的圆形缺陷段系数具有明显优势，识别结果倾向于判定为圆形缺陷. 将3种缺陷SDR数量对调，识别效果没有明显变化. 当3种缺陷SDR分别设定为27，27和26时，从识别结果看3种缺陷的识别率没有明显差别. 因此，为获得更好的识别效果，应保证组合后字典矩阵中各缺陷SDR大致持平，故令${C_{{d}}} = {L_{{d}}} = {N_{{d}}}{\text{ = }}{\kern 1pt} {\kern 1pt} {\kern 1pt} k$ .1.4 数据准备及评价指标
该文试验条件为Inter Core i7-9700、NIDIA GeForce GTX 1660、16GB内存、64位Windows操作系统、Visual Studio 2019，PyCharm2022.1.2. 为验证所提算法的有效性，对某石油钻采公司提供的小径管X射线图像进行识别试验，数据集为3535幅，大小为900像素 × 1200像素的焊缝图像. 在获取数据集后，利用该文提出的图像分割算法分割数据集图像，提取缺陷SDR并将SDR归一化为15 × 15的模板，保存在SDR数据库中. 随机提取SDR数据库中的40%构建字典矩阵，其余60%用以验证字典矩阵分类的有效性. 在对分类模型的性能进行描述时，选取混淆矩阵中的准确率
$A$ ，召回率$R$ ，精准率$P$ 和F1-score共4项指标，计算方式依照文献[12]，选取准确率$A$ 作为衡量分类模型性能的主要指标.2. 试验结果与分析
根据图8的K-SVD算法求解字典矩阵的算法分别求解圆形缺陷字典矩阵
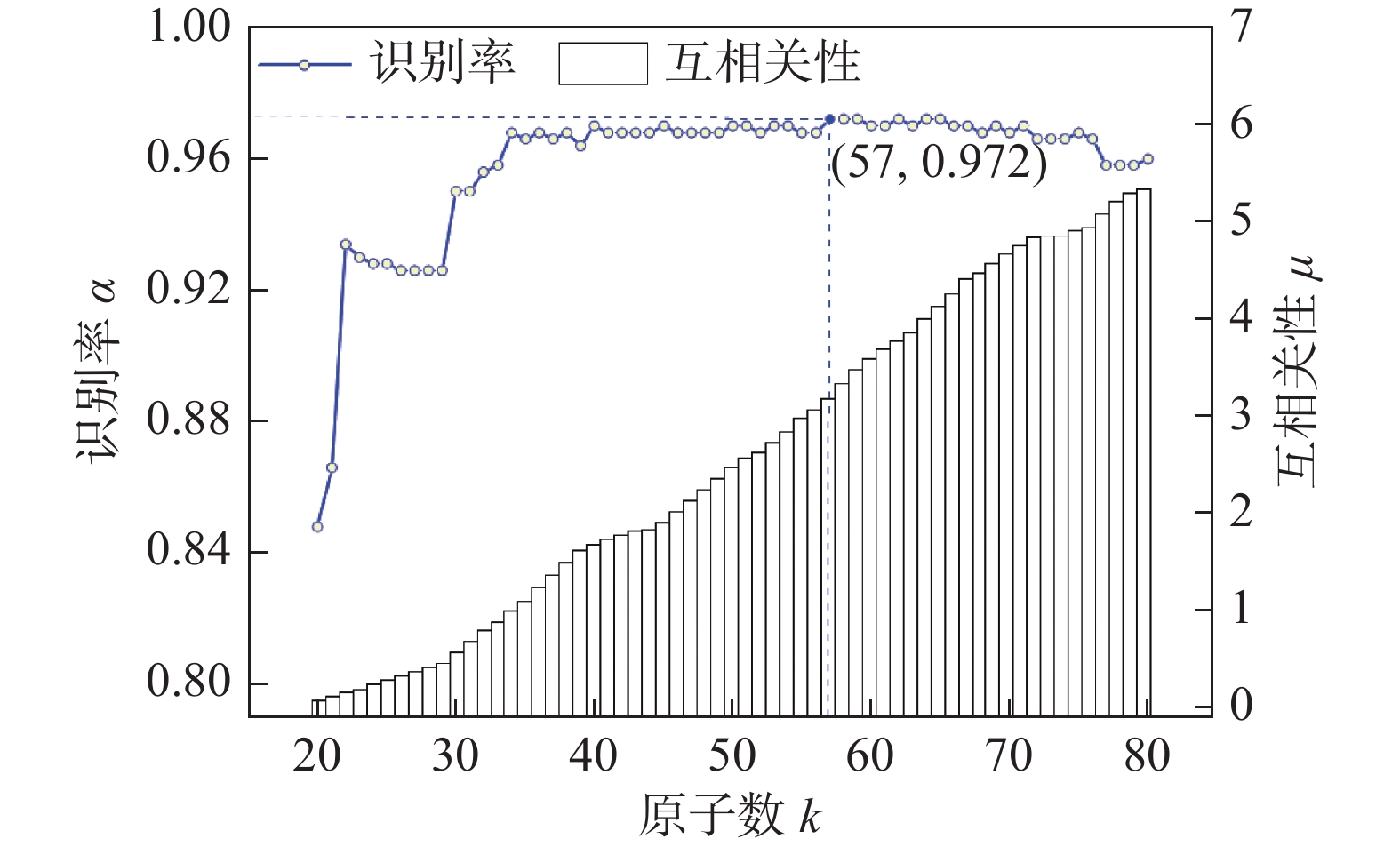
${{\boldsymbol{D}}_{{C}}}$ 、线形缺陷字典矩阵${{\boldsymbol{D}}_{{L}}}$ 和噪声字典矩阵${{\boldsymbol{D}}_{{N}}}$ ，并依据式(7)构成小径管X射线焊缝缺陷字典矩阵${\boldsymbol{D}}$ . 不同原子数下，字典矩阵${\boldsymbol{D}}$ 的识别率和3种缺陷原子间的互相关性如图9所示.![]()
图 9 缺陷识别率和不同类原子互相关性Figure 9. Defect recognition rate and the correlation of different kinds of atoms从图9可知，不同类型原子间的互相关性
$ \mu $ 随$k$ 值增大而增大. 当$k = 57$ 时，字典矩阵${\boldsymbol{D}}$ 的缺陷识别率达到最大值为97.2%，当$k$ 在一定范围内继续增大时，缺陷识别率在97%上下小幅震荡，在$k$ 值为58，59，62和64时识别率也可达到最大值，若$k$ 值增大到80附近，此时识别率因字典冗余性过大有所降低. 综上所述，从识别实时性以及不同类原子间互相关性最小两个角度考虑，应在保证识别率的前提下使$k$ 值尽可能小.选取
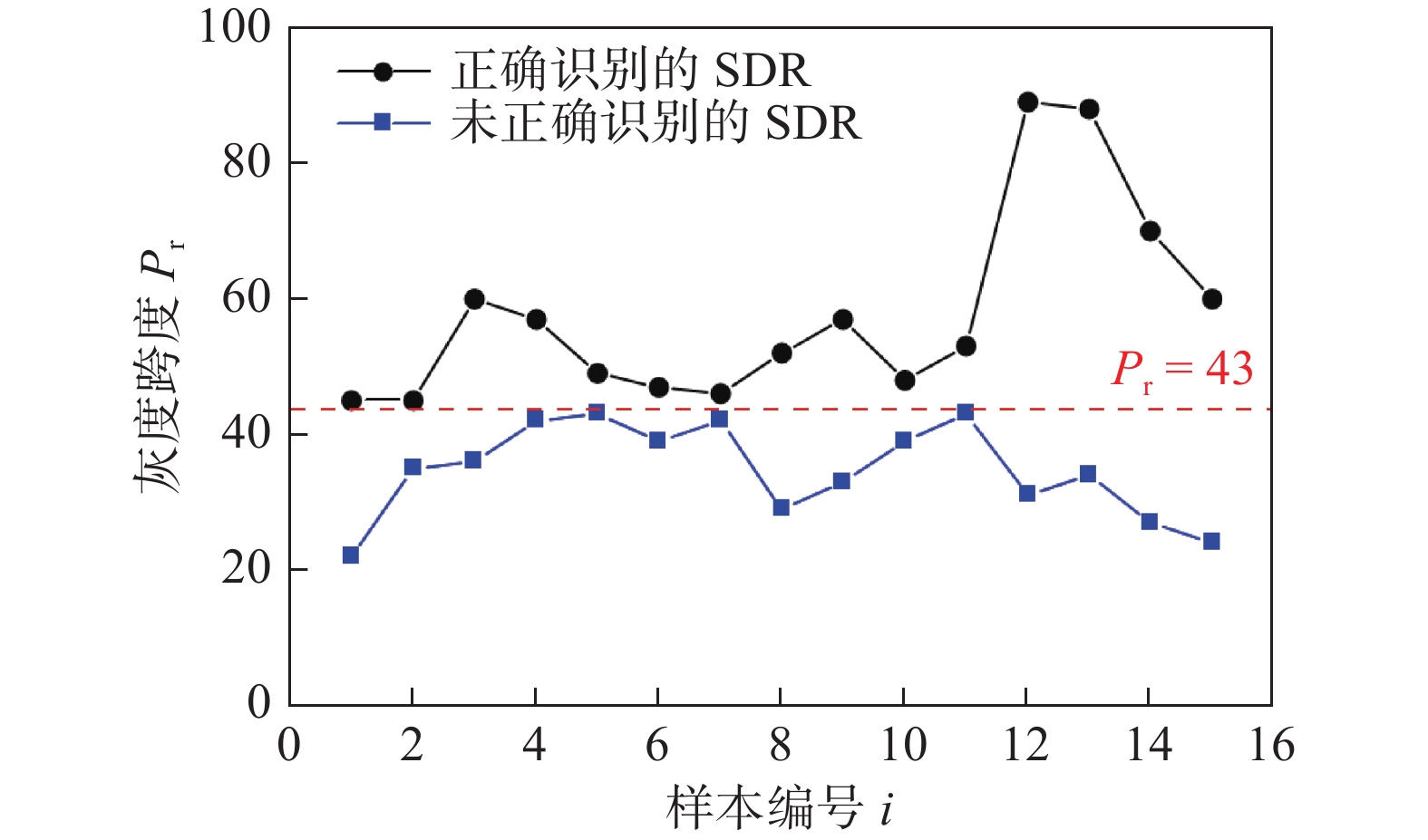
$k{\kern 1pt} {\kern 1pt} {\text{ = }}{\kern 1pt} {\kern 1pt} 57$ 作为最佳原子数，此时字典矩阵${\boldsymbol{D}}$ 的原子数为171. 使用字典矩阵${\boldsymbol{D}}$ 分别对圆形缺陷和线形缺陷的测试样本进行识别，圆形缺陷识别率为97.4%，线形缺陷识别率为96.7%，分类结果如表1所示，表1中混淆矩阵的4项指标为所有缺陷相对噪声. 实际试验中还发现一些未能正确识别的缺陷SDR，这些SDR或缺陷区域面积极小，或缺陷颜色较浅. 该文统计了未正确识别SDR的缺陷区域面积$d_S $ 归一化后和灰度跨度$P_{\rm{r}} $ ，正确识别SDR的缺陷区域面积$d_S $ 的统计结果与未正确识别SDR的缺陷区域面积$d_S $ 的统计结果对比如图10所示.正确识别的SDR的灰度跨度$ P_{\rm{r}}$ 的统计结果与未正确识别SDR的灰度跨度$ P_{\rm{r}} $ 的统计结果对比如图11所示. 由于数据量过小的原故，目前试验结果无法证明缺陷面积对识别准确率的影响，但从图11可知，正确识别的SDR与未正确识别的SDR在灰度跨度上具有明显差异，未正确识别的SDR灰度跨度普遍低于43. 究其原因，该文认为当图像灰度跨度低于43时，缺陷与背景间对比度较低，稀疏系数${\boldsymbol{X}}$ 中的非0值分布分散，因此识别时易产生误判. 数据库中也存在部分SDR表现出具有其它缺陷的图像特征，这种类型的缺陷在分类时更容易出错，对这种难以分类的SDR还需进行更加深入的研究. 所提算法包括ROI区域分割，SDR提取和缺陷识别共3个步骤，在算法运行过程中，步骤一耗时远大于步骤2和步骤3. 从系统实时性考虑，应使用GPU对步骤1进行加速，以处理1幅图像为例，平均加速效果如表2所示.表 1 测试分类结果Table 1. The results of test classification缺陷类型 缺陷数量 m(个) 缺陷识别率 α 准确率 A 召回率 R 精确率 P F1-score 圆形缺陷 线性缺陷 噪声 圆形 341 6 3 0.974 0.972 0.995 0.970 0.982 线形 8 232 0 0.967 噪声 6 12 132 0.880 表 2 算法加速效果Table 2. Algorithm acceleration effect算法步骤 GPU加速前耗时${{{t_1}} \mathord{\left/ {\vphantom {{{t_1}} s}} \right. } s}$ GPU加速后耗时${{{t_2}} \mathord{\left/ {\vphantom {{{t_2}} s}} \right. } s}$ ROI分割 31.44 1.12 SDR提取 4.37 — 缺陷识别 0.01 — 随着计算机和人工智能的发展，许多学者从传统的主观提取X射线焊缝图像特征，转向用自动学习的方式提取X射线焊缝图像特征[14-15]. 近年来，深度学习的发展也使越来越多的学者将各种不同的深度学习模型应用到自己的研究当中并取得优异的成果. 为了证明所提算法的优越性，将相同数据集在VGG16，GoogleNet，ResNet18和YoLo V3共4个网络模型上进行测试对比，结果如表3所示.
表 3 性能对比Table 3. Performance comparison算法模型 准确率 $ A(\%) $ 检测时间 $t{\text{/s}}$ VGG16 94.87 5.17 GoogleNet 95.57 1.36 ResNet18 96.38 1.47 YoLo V3 94.68 1.15 所提算法 97.20 5.50 从表3可以看出所提算法相比于一些深度学习模型对焊缝缺陷的检测精度更高，这可能是由于缺陷面积相对于图像过小导致深度学习模型无法提取有效特征的缘故，而稀疏字典学习由于不需要提取特征，因此相比于深度学习模型而言在解决小面积对象分类问题上更有优势. 从检测速度的角度出发，所提算法检测速度较慢，在之后的研究中可尝试通过深化程序的并行程度或者结合基于深度模型的图像分割方法加快检测速度.
3. 结论
(1) 采用两步图像分割法可准确提取出小径管焊缝图像感兴趣ROI，极大降低了提取SDR和缺陷分类的成本. 经过并行加速后，该分割方法在实际应用中是快速有效的，ROI分割时间降低为1.12 s，有效分割率达到98.6%.
(2)与深度学习方法相比，通过稀疏字典学习的方式对焊缝缺陷进行识别避免了特征提取的难题，学习成本更低，计算速度更快，准确率也更高，在实践中展现出了巨大的优越性.
(3)字典矩阵仅需较小的原子数就可以达到很高的缺陷识别准确率，即使学习过程完成，也可随时将典型缺陷原子加入字典，最终形成过完备字典.
-
![]()
图 1 小径管X射线图像
Figure 1. X-ray image of small diameter tube. (a) original image; (b) elliptical image with tilt radiography; (c) overlapping image with vertical radiography
![]()
图 2 ROI区域提取算例1
Figure 2. ROI extraction example 1. (a) original image; (b) segmented image
![]()
图 3 ROI区域提取算例2
Figure 3. ROI extraction example 2. (a) original image; (b) segmented image
![]()
图 4 ROI区域提取算例3
Figure 4. ROI extraction example 3. (a) original image; (b) segmented image
![]()
图 5 ROI区域提取算例4
Figure 5. ROI extraction example 4. (a) original image; (b) segmented image
![]()
图 7 疑似局部图像事例
Figure 7. Example of suspected defect region. (a) SDR of round defects; (b) SDR of linear defects; (c) SDR of noise
![]()
图 9 缺陷识别率和不同类原子互相关性
Figure 9. Defect recognition rate and the correlation of different kinds of atoms
表 1 测试分类结果
Table 1 The results of test classification
缺陷类型 缺陷数量 m(个) 缺陷识别率 α 准确率 A 召回率 R 精确率 P F1-score 圆形缺陷 线性缺陷 噪声 圆形 341 6 3 0.974 0.972 0.995 0.970 0.982 线形 8 232 0 0.967 噪声 6 12 132 0.880 
下载: 导出CSV
表 2 算法加速效果
Table 2 Algorithm acceleration effect
算法步骤 GPU加速前耗时${{{t_1}} \mathord{\left/ {\vphantom {{{t_1}} s}} \right. } s}$ GPU加速后耗时${{{t_2}} \mathord{\left/ {\vphantom {{{t_2}} s}} \right. } s}$ ROI分割 31.44 1.12 SDR提取 4.37 — 缺陷识别 0.01 —
下载: 导出CSV
表 3 性能对比
Table 3 Performance comparison
算法模型 准确率 $ A(\%) $ 检测时间 $t{\text{/s}}$ VGG16 94.87 5.17 GoogleNet 95.57 1.36 ResNet18 96.38 1.47 YoLo V3 94.68 1.15 所提算法 97.20 5.50
下载: 导出CSV
-
[1] 周兆逸, 张亚南, 王肖锋, 等. 基于改正二维主成分分析的焊缝表面缺陷检测[J]. 焊接学报, 2021, 42(11): 70 − 76. Zhou Zhaoyi, Zhang Yanan, Wang Xiaofeng, et al. Weld surface defect detection based on improved two dimensional principal c-omponent analysis[J]. Transactions of the China Welding Institution, 2021, 42(11): 70 − 76.
[2] Yang L, Wang H X, Huo B Y, et al. An automatic welding defect location algorithm based on deep learning[J]. NDT & E International:Independent Nondestructive Testing and Evaluation, 2021, 120: 102435.
[3] Sun J, Li C, Wu X J, et al. An Effective method of weld defect detection and classification based on machine vision[J]. Ieee Transactions on Industrial Informatics, 2019, 15(12): 6322 − 6333. doi: 10.1109/TII.2019.2896357
[4] Zhang Y, You D, Gao X, et al. Welding defects detectionbased on deep learning with multiple optical sensors during disklaser welding of thick plates[J]. Journal of Manufacturing Systems, 2019, 51: 87 − 94. doi: 10.1016/j.jmsy.2019.02.004
[5] 魏博文, 高炜欣, 刘梦溪. 激光超声结合CNN的铸件缺陷检测方法[J]. 激光与红外, 2022, 52(9): 1327 − 1334. doi: 10.3969/j.issn.1001-5078.2022.09.009 Wei Bowen, Gao Weixin, Liu Mengxi. Casting defect detection method combined with laser ultrasound and convolutional neural network[J]. Laser & Infrared, 2022, 52(9): 1327 − 1334. doi: 10.3969/j.issn.1001-5078.2022.09.009
[6] Zhang L, Zhang Y J, Dai B C, et al. Welding defect detectionbased on local image enhancement[J]. IET Image Processing, 2019, 13(13): 2647 − 2658. doi: 10.1049/iet-ipr.2018.5840
[7] 江野, 王东, 秦小阳, 等. 奥氏体异种钢薄壁小径管焊缝裂纹超声相控阵检测[J]. 焊接学报, 2018, 39(8): 119 − 122. Jiang Ye, Wang Dong, Qin Xiaoyang, et al. Ultrasonic phased array inspection on welded crack of austenitic dissimilar ateel with thinwall and small diameter tube[J]. Transactions of the China Welding Institution, 2018, 39(8): 119 − 122.
[8] 陈小明, 谭云华, 赖传理, 等. 相控阵技术在超小径管焊缝检测应用研究[J]. 锅炉技术, 2021, 52(S1): 55 − 58. Chen Xiaoming, Tan Yunhua, Lai Chuanli, et al. The reserch of phased array testing on the butt weld of tube[J]. Boiler Technology, 2021, 52(S1): 55 − 58.
[9] Xie L, Wang T, Zhang Y. Comparative experimental study on phased array and X-ray detection of small diameter pipe weld[J]. Journal of Physics, 2021, 1885(3): 032023.
[10] 贾潇, 赵隆. 相控阵超声与射线检测对石油化工管道缺陷检测的对比分析[J]. 中国石油和化工标准与质量, 2022, 42(15): 174 − 175. Jia Xiao, Zhao Long. Comparative analysis of ultrasonic phasedarray and X-ray detection for petrochemical pipeline defect dete-ction[J]. China Petroleum and Chemical Standard and Quality, 2022, 42(15): 174 − 175.
[11] 张小琳, 刘祎, 白贇沨, 等. 基于背景估计的焊缝缺陷检测[J]. 电子测量技术, 2022, 45(14): 116 − 122. Zhang Xiaolin, Liu Yi, Bai Yunfeng, et al. Weld defect detectionbased on background estimation[J]. Electronic Measurement Technology, 2022, 45(14): 116 − 122.
[12] 高炜欣, 胡玉衡, 穆向阳, 等. 基于聚类的埋弧焊X射线焊缝图像缺陷分割算法及缺陷模型[J]. 焊接学报, 2012, 33(4): 37 − 41. Gao Weixin, Hu Yuheng, Mu Xiangyang, et al. Study on sub-arc X-ray welding image defect segmentation algorithm and defectmodel[J]. Transactions of the China Welding Institution, 2012, 33(4): 37 − 41.
[13] 孙春红, 丁广太, 方坤. 基于稀疏字典学习的羊绒与羊毛分类[J]. 纺织学报, 2022, 43(4): 28 − 32. Sun Cunhong, Ding Guangtai, Fang Kun. Cashmere and wool classification based on sparse dictionary learning[J]. Journal of Textile Research, 2022, 43(4): 28 − 32.
[14] Hou W H, Zhang D S, Wei Y, et al. Review on computer aided weld defect detection from radiography images[J]. Applied Sciences, 2020, 10(5): 1878 − 1893. doi: 10.3390/app10051878
[15] 修延飞, 李海超, 胡广泽, 等. 一种用于穿孔塞焊焊缝特征提取的视觉识别算法[J]. 焊接学报, 2020, 41(2): 75 − 79. doi: 10.12073/j.hjxb.20190927002 Xiu Yuanfei, Li Haichao, Hu Guangze, et al. A visual recognition algorithms for seam feature extraction of perforated plug welding[J]. Transactions of the China Welding Institution, 2020, 41(2): 75 − 79. doi: 10.12073/j.hjxb.20190927002
-
期刊类型引用(4)
1. 朱新杰，李永涛，邓明晰，姚森，张洁. 焊缝散射条件下板中超声导波直线阵列多帧变秩成像检测. 焊接学报. 2025(01): 80-86 . 
本站查看
2. 宋艳艳，王泽民，叶振宇，陈乐. 基于视觉软件的小径管对接焊缝DR图像缺陷自动识别. 上海化工. 2025(02): 44-48 . 百度学术
3. 李兴红. 基于深度学习的液氯罐车射线图像缺陷自动识别研究. 中国高新科技. 2024(12): 15-17 . 百度学术
4. 程希莹，何云凯，吴晗宇. 基于深度学习的焊缝X射线图像缺陷识别. 淮阴师范学院学报(自然科学版). 2024(04): 319-328 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 130
- HTML全文浏览量: 46
- PDF下载量: 31
- 被引次数: 4
