Evaluating solidification cracking susceptibility of Mg alloys and intergranular liquid backfilling during welding
-
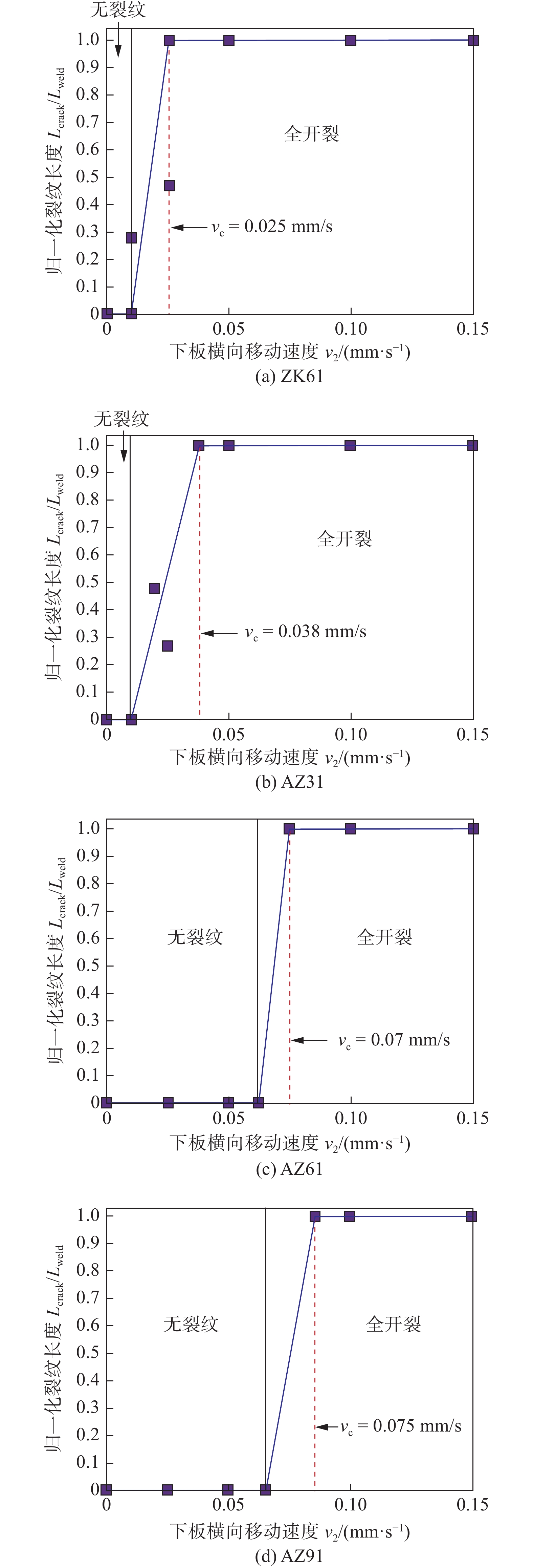
摘要: 试验选用ZK61, AZ31, AZ61和AZ91镁合金进行焊接凝固裂纹敏感性的分析. 首先进行了双速模式下的横向移动裂纹敏感性试验，获得了4种镁合金的临界横向移动速度，并对凝固裂纹敏感性进行了评估和排序：ZK61 > AZ31 > AZ61 > AZ91，与单速模式试验结果以及基于│dT/d(fS)1/2│max作为裂纹敏感指数得到的计算预测结果一致，验证了双速模式的横向移动裂纹敏感性试验用于评估镁合金凝固裂纹敏感性的有效性.凝固裂纹尖端及周边存在液相回填特征，ZK61镁合金的晶间回填液相呈非连续状且回填通道较窄，难以起到愈合裂纹效果，增大了凝固裂纹敏感性；AZ91镁合金液相回填通道宽度最大，有利于晶间液相回填，降低了凝固裂纹敏感性.Abstract: In present work, the widely used Mg alloys ZK61, AZ31, AZ61 and AZ91 were selected for investigating the solidification cracking susceptibility during welding. Transverse motion weldability (TMW) test in two-speed mode was used to evaluate the susceptibility of Mg alloys to solidification cracking during welding. The critical transverse moving speed was obtained and considered as an index to estimate the solidification cracking susceptibility of Mg alloys as ranking: ZK61 > AZ31 > AZ61 > AZ91. The ranking is consistent with the results of one-speed test and predicted results based on │dT/d(fS)1/2│max. It was shown that two-speed test of TMW is effective to evaluate the susceptibility of Mg alloys to solidification cracking. According to the backfilled liquid at the tip of or near the solidification cracking, the intergranular backfilled liquid of ZK61 is discontinuous and the channel is narrow, which is difficult to heal the crack and increases the solidification cracking susceptibility. The liquid backfilling channel of AZ91 is the widest, which is conducive to intergranular liquid backfilling and reduces the solidification crack susceptibility.
-
Keywords:
- magnesium alloy /
- welding /
- solidification cracking /
- intergranular liquid
-
0. 序言
航空发动机上各种功能用途的安装座大多通过焊接与机匣壳体相连接，在实际工作当中，机匣壳体会承受多种载荷的周期性作用，从而导致这些安装座的环形焊缝很容易成为多轴疲劳破坏的薄弱部位，因此，精确评估机匣安装座环形焊缝在复杂载荷下的多轴疲劳寿命，对于提高发动机结构强度和可靠性有非常重要的意义.
常用的焊接接头疲劳寿命预测方法主要包括：名义应力法、局部应力应变法[1]、热点应力法[2]、场强法[3]、断裂力学法[4]等，这些方法运用简单且实用，但是不能表征焊接接头多轴疲劳的损伤机理，随着Brown等人[5]提出临界面法后，多轴疲劳寿命研究的主要方法开始逐步转变成临界面法，相较于传统的疲劳寿命预测方法，临界面法更能解释焊接接头的多轴疲劳损伤机理，也更具有现实的物理意义.
根据工程实际的需要，目前较为广泛的是针对焊接接头拉-扭多轴疲劳寿命的研究，王霄翔[6]、顾明恒[7]、刘亮[8]分别进行了3种材料的真空电子束焊接头薄壁圆管件的拉-扭多轴疲劳试验，通过临界面法研究了焊接接头的多轴疲劳寿命，而针对弯-扭多轴疲劳试验研究焊接接头多轴疲劳寿命，则主要以角接接头为主；赵一阳[9]、邬婷[10]提出一种多轴疲劳寿命预测方法，分别选用十字和T形焊接接头、法兰管焊接结构作为研究对象，通过有限元数值模拟方法计算弯-扭组合加载下的疲劳寿命，通过与单轴试验的数据结果进行对照，证明该预测方法的有效性；刘健[11]选取4种焊接接头试件进行弯-扭多轴疲劳试验，采用缺口应力法和多轴疲劳准则预测不同焊接接头试件的多轴疲劳寿命，而关于采用双轴拉伸疲劳试验研究焊接结构的多轴疲劳，主要以研究疲劳裂纹扩展规律为主；Abecassis等人[12]通过异种金属焊接接头以及这两种材料焊接接头的十字形双轴拉伸试件的等双轴拉伸疲劳载荷下的疲劳试验，研究了I + II型裂纹组合对疲劳裂纹行为的影响规律；Koji等人[13]通过不同相位条件下的双轴拉伸疲劳试验，研究了角接接头的双轴载荷下疲劳裂纹扩展行为；Shanyavskiy[14]提出使用十字形双轴拉伸焊接试件来模拟薄壁压力容器筒体焊缝应力状态，利用J积分、应变能原理研究了焊接件在双轴拉伸疲劳载荷下的疲劳裂纹扩展规律.
国内外对焊接接头多轴疲劳研究已开展了一些工作，但大都采用拉-扭和弯-扭加载的形式，对于类似于机匣安装座环形焊缝在双轴拉伸载荷下的疲劳寿命研究，还鲜有报道. 论文将以GH4169环形电子束焊接结构为研究对象，对其双轴拉伸载荷下的疲劳寿命预测方法开展研究，提出一个行之有效的疲劳寿命预测模型研究方法.
1. 双轴拉伸疲劳试验
1.1 试验件
针对航空发动机大型零部件疲劳寿命的分析，由于实际工作时的应力状态较为复杂，仅采用标准件进行疲劳试验无法得到精确可靠的疲劳寿命评估结果[15]，而如果直接采用零部件进行试验，则会产生制造成本较高、加工周期长、试验工装难以控制等问题. 近年来，国内外研究者通常设计出带结构特征的模拟件，对大型零部件某些重点关注的危险部位的疲劳寿命进行考核[16-17]，由于模拟件能够很好反映构件的疲劳损伤特征，从而对零组件的疲劳寿命预测结果有较高的可信度. 对于机匣安装座环形焊缝的疲劳性能研究而言，以往大都是以单轴拉伸疲劳试验为主[18]，但是单轴疲劳试验并不能真实地反映安装座环形焊缝处的疲劳损伤特征. 根据课题组之前的研究成果[19]，以传统的十字形双轴试件为基础，针对圆柱形机匣安装座进行改进，设计出带有机匣安装座环形焊缝结构特征的疲劳试验件，如图1所示， 试验件轮廓尺寸为144 mm × 144 mm × 3.5 mm，中心试验区的直径为39.5 mm，厚度为1.2 mm，安装座附近环形阴影部位为焊缝区，焊缝直径为29 mm，包含焊缝、熔合区和热影响区的径向宽度为3 mm. 两相邻夹持臂之间圆弧过渡段半径为20 mm，中心试验区正反面减薄过渡倒角半径R为6 mm，安装座结构根部的倒角半径为10.5 mm，通孔直径为3 mm，夹持臂楔形角度为50°，减薄区最外圆的直径为39.5 mm.
1.2 试验件材料
GH4169高温合金因其在650 ℃下有极高的屈服强度，且在焊接加工之后焊接接头有良好的塑性性能，广泛被运用在航空发动机的高温部件中，此外，GH4169高温合金也有较高的耐腐蚀、抗氧化和耐辐射性能，使得GH4169制造的构件能够在复杂的工况条件下，也有着优异的可靠性以及较高的结构强度，文中采用GH4169加工试验件，实物图如图2所示.
![]()
图 2 双轴拉伸试验件实物图Figure 2. Physical image of cruciform specimen. (a) front; (b) opposite1.3 试验方案
试验在西安交通大学的机械结构强度与振动国家重点实验室完成，采用的设备为MTS Biaxial平面双轴试验系统，该试验系统能实现双轴及多轴的拉压、扭转、高低温等复杂加载组合试验，试验机共4个夹头，水平x方向2个作动器，竖直y方向2个作动器，并配有温度环境箱，如图3所示.
双轴拉伸疲劳试验的试验温度为室温，采用应力控制，并且x轴与y轴的作动器施加等比例循环载荷，试验的载荷波形为正弦波，载荷比R = 0.1，由于疲劳寿命主要处于高周范围，因此试验频率的选择尽量考虑较高试验频率，加载频率15 Hz.
试验根据GH4169焊接接头力学性能参数设定了5个等轴加载(双轴比γ = 1)的载荷水平：(40 kN/40 kN),(33.3 kN/33.3 kN)，(26.7 kN/26.7 kN)，(21.3 kN/21.3 kN)，(16.7 kN/16.7 kN)，此外，还设定了两种非等轴的加载方式：(γ = 0.8，26.7 kN/21.4 kN)，(γ = 0.6，26.7 kN/16 kN)，所有施加的具体载荷大小均根据实际加工误差进行修正.
2. 试验结果
2.1 试验结果分析
根据试验结果可知，试件的疲劳寿命主要在104周次 ~ 106周次， 由于试验为双轴拉伸疲劳试验，在拟合S-N曲线的时候可以采用Von Mises等效应力作为疲劳损伤参量，将多轴的疲劳损伤等效成单轴的疲劳损伤，因此，论文将结合等效应力准则与Basquin方程，建立S-N曲线.
$$ {\text{lg}}\sigma {\text{ = }}a + b\lg {N_{\rm{f}}} $$ (1) 式中：Nf为疲劳寿命；σ为应力值；a和b为拟合参数，根据不同载荷水平下对应的焊缝处最高等效应力值以及试验结果的有效数据，采用最小二乘法在双对数坐标系下对数据进行线性回归拟合，得到双轴拉伸疲劳S-N曲线，如图4所示.
根据拟合出来的结果，得到S-N曲线方程，即
$$ {\text{lg}}\sigma {\text{ = }}3.752\;3 - 0.209\;98\lg {N_{\rm{f}}} $$ (2) 图5为采用等效应力作为疲劳损伤参量试件疲劳寿命的结果，可以看到双轴比γ = 0.8的预测结果在3倍分散带以内，其余两种双轴比均存在部分数据点在3倍分散带以外的情况，因此等效应力作为疲劳损伤参量预测双轴拉伸疲劳寿命并不理想.
2.2 宏观断口分析
试验结果显示从焊缝处断裂的试验件，其疲劳断裂过程均位于焊缝上拉伸轴的某点处开始裂纹萌生，沿着环形焊缝向两侧开始扩展，直至最终失稳断裂. 图6为典型试件的疲劳断裂过程.
![]()
图 6 等轴加载试验件断裂过程示意图Figure 6. Fracture process of specimen under equiaxial loading. (a) N = 601 220; (b) N = 630 520; (c) N = 635 874; (d) N = 643 599载荷循环为601 220周次时，正y轴12点钟方向焊缝上出现了一处裂纹萌生的地方，图5(a)中的A点，随着循环载荷的继续作用，该处裂纹源沿着焊缝向两侧扩展；载荷循环为630 520周次时，裂纹逐渐扩大并开始向两端圆弧过渡段扩展；载荷循环为635 874周次时，裂纹已经趋于断裂并形成一条横向的大裂纹，最后载荷循环为643 599周次时完全断裂.
其他有效试验件的裂纹萌生、扩展过程均与此相似，所不同的是萌生点位会在12点，3点，6点，9点钟方向随机出现，最终均表现为垂直某一拉伸轴的横向断裂. 图7是试验件非等轴加载下的断口对接示意图，观察裂纹位置可以发现，裂纹均处于x轴上，这是由于x轴施加的载荷高于y轴，造成x轴上焊缝的应力水平高于y轴. 通过观察所有试验件断口的对接情况可以发现，焊缝处裂纹两侧断口对接的缝隙较大，而圆弧过渡段的断口齐平且吻合程度较好，说明焊缝处是裂纹的扩展区而圆弧过渡段处为裂纹的瞬断区.
![]()
图 7 非等轴加载试验件断口对接示意图Figure 7. Fracture docking of specimen under unequiaxial loading. (a) γ=0.8;(b) γ=0.6试验件疲劳断口主要分为疲劳源区、扩展区和瞬断区，图8为模拟件典型宏观断口的形貌，观察可知，点A处的断口表面相对平整光滑，可以判断该处为裂纹源，点B处的断口有凹凸不平的疲劳弧线，可以判断为扩展区，点C处的断口表面发白且粗糙，可以判断为瞬断区.
3. 多轴疲劳寿命预测模型
3.1 基于Findley准则的多轴疲劳寿命预测模型
Findley[20]在分析了多数疲劳试验数据后，提出了一种疲劳损伤准则，认为剪应力是引起疲劳破坏的主要因素，因此，将剪应力幅值τa和法向正应力值σn的线性组合作为疲劳的损伤参量，通过计算不同平面下该损伤参量的数值，并从中筛选出最大损伤平面，即确定了临界平面，Findley准则的多轴疲劳寿命预测模型公式为
$$ \max {\left( {{\tau _{\rm{a}}} + k{\sigma _{\rm{n}}}} \right)_{\theta ,\phi }} = f\left( {{N_{\rm{f}}}} \right) $$ (3) 式中：等式右边为疲劳寿命Nf为变量的函数；θ和ϕ为确定临界平面的旋转角度；k表示临界平面上正应力对疲劳损伤的所占权重的材料参数，根据该材料的试验数据，将参数k的值设为1.
根据Findley准则定义的临界平面确定方法，需要先计算试验件焊缝的最危险节点不同平面下的剪应力幅值τa和法向正应力σn之和，再将这些数据点整合到同一个坐标系下，如图9所示，最后寻找数值最大的数据点所对应的平面.
如图9中可以看到，Findley准则下存在两个最大损伤平面，分别为原坐标系θ旋转22°且ϕ旋转180°的平面，以及θ旋转157°且ϕ旋转0°的平面，任意选取一个损伤平面作为临界平面，再提取该临界平面下的剪应力幅值τa和法向正应力σn，计算Findley准则的疲劳损伤参量，与等效应力作为疲劳损伤参量预测疲劳寿命相同，结合Basquin公式得到疲劳寿命预测方程，即
$$ \lg \left( {{N_{\rm{f}}}} \right){\text{ = }}18.359\;4 - 4.753\;1\lg \left[ {{\text{max}}{{\left( {{\tau _{\rm{a}}} + {\sigma _{\rm{n}}}} \right)}_{\theta ,\phi }}} \right] $$ (4) 该模型预测疲劳的结果如图10所示，与等效应力准则相似，预测结果并不理想，双轴比γ = 0.6的部分数据结果在3倍分散带以外.
3.2 基于Matake准则的多轴疲劳寿命预测模型
与Findley准则不同的是，Matake[21]认为剪应力幅值最大值的平面是多轴疲劳的最大损伤平面，因此，将Findley准则中的临界平面定义为剪应力幅值最大的平面，并将该平面上的剪应力幅值τa和法向正应力σn的线性组合定义为疲劳损伤参量为
$$ \max {\left( {{\tau _{\rm{a}}}} \right)_{\theta ,\phi }} + k{\sigma _{\rm{n}}} = f\left( {{N_{\rm{f}}}} \right) $$ (5) 式中：所有参数的含义与Findley准则均相同，且经验参数k的取值仍然取1， Matake准则需要计算试验件焊缝的最危险节点各个平面的剪应力幅值，然后把所有平面的剪应力幅值整合到同一个坐标系下，如图11所示，最后寻找数值最大的数据点所对应的平面确定临界平面
从图11中可以看到，Matake准则下同样存在两个最大损伤平面，分别为原坐标系θ旋转45°且ϕ旋转180°的平面，以及θ旋转135°且ϕ旋转0°的平面，任意选取一个损伤平面作为临界平面，提取该临界平面下的剪应力幅τa和法向正应力σn计算Matake疲劳损伤参量，得到疲劳寿命预测模型为
$$ \lg \left( {{N_{\rm{f}}}} \right) = 18.132\;7 - 4.756\;1\lg \left[ {\max {{\left( {{\tau _{\rm{a}}}} \right)}_{\theta ,\phi }} + {\sigma _{\rm{n}}}} \right] $$ (6) 通过该模型预测试验件的疲劳寿命，如图12所示，可以看到，预测结果与Findley准则相差并不明显，而双轴比γ = 0.6的寿命预测略有提高，这说明剪应力幅值的确对试验件的其他双轴比的疲劳寿命产生了一定影响，但整体的预测结果仍然不够理想，因此，使用Matake准则下的疲劳寿命预测模型同样无法很好地对所有情况进行寿命预测.
3.3 基于修正的Matake准则的多轴疲劳寿命预测模型
从上述两种临界平面法准则的疲劳寿命预测结果对比可以看出，剪应力幅值对于焊缝多轴疲劳寿命是有一定影响的，造成分散性的主要原因在于双轴比γ的变化，因此基于Matake疲劳寿命预测模型进行修正，以适合不同双轴比下试验件焊缝的疲劳寿命预测. Matake准则中k根据经验选取1，但是该值并不能反映不同双轴比对焊缝多轴疲劳寿命的影响，而将双轴比γ作为修正参量引入k中是比较合理的. 此外，从上述的分析结果可以看到，不同双轴比下的剪应力对于试验件焊缝的疲劳寿命的影响是更明显的，为了减少正应力对于寿命预测结果的干扰，引入剪应力与正应力的比值$ \lambda $来修正疲劳损伤参量. 根据试验件3种双轴比的寿命预测结果可以看出，双轴比γ为0.8的预测结果是较好，因此以γ = 0.8为基础对k进行修正，综上所述，修正后的Matake准则为
$$ {\sigma _{{\rm{em}}}} = \max {\left( {{\tau _{\rm{a}}}} \right)_{\theta ,\phi }} + \Delta k \cdot {\sigma _{\rm{n}}} = f\left( {{N_{\rm{f}}}} \right) $$ (7) 式中：$ {\sigma _{{\rm{em}}}} $为修正的Matake准则疲劳损伤参量，$ \Delta k $为修正后的k值，即
$$ \Delta k = 1 + \lambda \frac{{\left( {\gamma - 0.8} \right)}}{{0.8}} $$ (8) 式中：$ \lambda $为临界平面上剪应力幅值与正应力比值，即
$$ \lambda {\text{ = }}\frac{{{\tau _{\rm{a}}}}}{{{\sigma _{\rm{n}}}}} $$ (9) 由于是基于Matake准则进行修正的，因此所选取的临界平面与Matake准则相同. 提取临界平面上的剪应力幅值和正应力，计算修正后的疲劳损伤参量$ {\sigma _{{\rm{em}}}} $，得到修正后的Matake疲劳寿命预测模型，即
$$ \begin{split} \lg \left( {{N_{\rm{f}}}} \right) = 18.239\;2 - 4.767\;8\lg \left\{ {\max {{\left( {{\tau _{\rm{a}}}} \right)}_{\theta ,\phi }} + \left[ {1 + \left( {\frac{{{\tau _{\rm{a}}}}}{{{\sigma _{\rm{n}}}}}} \right) \cdot \frac{{\left( {\gamma - 0.8} \right)}}{{0.8}}} \right] \cdot {\sigma _{\rm{n}}}} \right\} \end{split} $$ (10) 为验证修正后的Matake准则提出的疲劳损伤参量能够解释双轴比对双轴拉伸疲劳寿命的影响，同样给出了3种双轴比加载下1/4焊缝路径的$ {\sigma _{{\rm{em}}}} $变化，如图13所示.
从图中焊缝最危险点A的$ {\sigma _{{\rm{em}}}} $变化可以看到，双轴比γ为1时，最大的$ {\sigma _{{\rm{em}}}} $与另外两种双轴比γ较为接近，符合实际试验中寿命的变化规律，证明了修正后的Matake准则能够解释双轴比对于双轴拉伸疲劳寿命的影响， 通过修正的Matake疲劳寿命预测模型进行疲劳寿命预测，如图14所示.
![]()
图 14 修正的Matake准则下疲劳寿命预测结果Figure 14. Fatigue life prediction with modified Matake criteria从图中可以看到，所有的预测结果都已经在3倍分散带以内，特别是双轴比γ为0.6预测结果有了较大的改善，说明修正后的疲劳寿命预测模型基本上满足了3种双轴比的疲劳寿命预测要求，具有较好的预测精度.
4. 结论
(1) 等效应力作为损伤参量对双轴比γ不为1的疲劳寿命预测结果并不理想，并且难以反映不同双轴比对双轴拉伸疲劳寿命的影响.
(2) Findley准则与Matake准则整体的疲劳寿命预测结果相差并不明显，但是针对非等轴加载的情况，Matake准则的疲劳寿命预测结果略有提高，验证了剪应力幅值对双轴拉伸疲劳有一定的影响.
(3)采用修正的Matake的疲劳寿命预测模型比其他疲劳寿命预测模型的预测精度更高，所有的预测数据点都能在3倍分散带以内，并且修正后的参数k考虑了双轴比的影响以及剪应力与正应力之间的关系，更具有实际物理意义.
-
![]()
图 1 横向移动裂纹敏感性试验
Figure 1. Transverse motion weldability (TMW) test. (a) schematic diagram of one-speed test; (b) schematic diagram of two-speed test; (c) one-speed test of ZK61 Mg alloy (v = 0.05 mm/s); (d) two-speed test of ZK61 Mg alloy (v1 = 0.7 mm/s, v2 = 0.05 mm/s)
![]()
图 2 镁合金凝固裂纹断口表面形貌
Figure 2. Fracture surface of Mg alloys. (a) dendritic fracture surface; (b) α-Mg dendrites and liquid film
![]()
图 3 横向移动裂纹敏感性试验的裂纹长度归一化裂纹长度
Figure 3. Normalized crack length after TMW test (ZK61 at two-speed test). (a) overview; (b) close-up view
![]()
图 4 镁合金焊接凝固裂纹敏感性测试结果(双速模式)
Figure 4. Two-speed testing results of Mg alloys. (a) ZK61; (b) AZ31; (c) AZ61; (d) AZ91
![]()
图 5 基于临界横向移动速度镁合金裂纹敏感性与预测结果
Figure 5. Ranking of solidification cracking susceptibility based on critical transverse motion speed consistent with predicted results. (a) one-speed test results; (b) two-speed test results; (c) T ~ (fs)1/2 curve; (d) predicted results
![]()
图 6 镁合金焊缝横截面凝固裂纹特征及微观组织
Figure 6. Solidification cracking and microstructure on cross-section of Mg alloys weld. (a) schematic diagram of crack opening; (b) AZ31; (c) AZ91
![]()
图 7 镁合金凝固裂纹的液相回填及晶间共晶组织
Figure 7. Backfilled liquid and intergranular eutectic microstructure near solidification cracking. (a) ZK61; (b) AZ31; (c) AZ61; (d) AZ91
表 1 镁合金化学成分(质量分数，%)
Table 1 Chemical compositions of Mg alloys
合金 Al Zn Mn Fe Si Ni Cu Zr Mg ZK61 0.01 5.65 0.014 0.005 0.01 0.005 0.04 0.54 余量 AZ31 3.02 0.82 0.22 0.0027 0.0086 0.0048 0.0021 — 余量 AZ61 5.86 0.87 0.18 0.0042 0.0093 0.0064 0.0014 — 余量 AZ91 8.89 0.89 0.14 0.0042 0.0129 0.0107 0.0043 — 余量 
下载: 导出CSV
-
[1] Song J F, Pan F S, Jiang B, et al. A review on hot tearing of magnesium alloys[J]. Journal of Magnesium and Alloys, 2016, 4(3): 151 − 172. doi: 10.1016/j.jma.2016.08.003
[2] 闫志峰, 王卓然, 王树邦, 等. AZ31镁合金双面对称搅拌摩擦焊接头疲劳性能[J]. 焊接学报, 2022, 43(6): 61 − 68. Yan Zhifeng, Wang Zhuoran, Wang Shubang, et al. Fatigue properties of AZ31 magnesium alloy welded joint by double-sided friction stir welding[J]. Transactions of the China Welding Institution, 2022, 43(6): 61 − 68.
[3] 陈怡, 郭龙涛, 祁同福, 等. 镁合金铸件氦-氩保护TIG焊修复工艺[J]. 焊接学报, 2021, 42(9): 35 − 41. doi: 10.12073/j.hjxb.20201223001 Chen Yi, Guo Longtao, Qi Tongfu, et al. Repair process of magnesium alloy casting by He-Ar mixed gas TIG welding[J]. Transactions of the China Welding Institution, 2021, 42(9): 35 − 41. doi: 10.12073/j.hjxb.20201223001
[4] Liu L M, Welding and joining of magnesium alloys[M]. Cambridge: Woodhead Publishing, 2010.
[5] Liu K, Kou S. Susceptibility of magnesium alloys to solidification cracking[J]. Science and Technology of Welding and Joining, 2020, 25(3): 251 − 257. doi: 10.1080/13621718.2019.1681160
[6] Kou S. Welding metallurgy[M]. 3 rd edition. Hoboken N J: John Wiley and Sons, 2020.
[7] Kou S. A criterion for cracking during solidification[J]. Acta Materialia, 2015, 88: 366 − 374. doi: 10.1016/j.actamat.2015.01.034
[8] Clyne T W, Davies G J. The influence of composition on solidification cracking susceptibility in binary alloy systems[J]. 1981, Br Foundryman, 74: 65 − 73
[9] Kou S. A simple index for predicting the susceptibility to solidification cracking[J]. Welding Journal, 2015, 94: 374s − 388s.
[10] Liu J W, Kou S. Effect of diffusion on susceptibility to cracking during solidification[J]. Acta Materialia, 2015, 100: 359 − 368. doi: 10.1016/j.actamat.2015.08.064
[11] Liu J W, Kou S. Susceptibility of ternary aluminum alloys to cracking during solidification[J]. Acta Materialia, 2017, 125: 513 − 523. doi: 10.1016/j.actamat.2016.12.028
[12] Soysal T, Kou S. Predicting effect of filler metals on solidification cracking susceptibility of 2024 Al and 6061 Al[J]. Science and Technology of Welding and Joining, 2019, 24(6): 559 − 565. doi: 10.1080/13621718.2019.1570683
[13] Soysal T, Kou S. Effect of filler metals on solidification cracking susceptibility of Al alloys 2024 and 6061[J]. Journal of Materials Processing Technology, 2019, 266: 421 − 428. doi: 10.1016/j.jmatprotec.2018.11.022
[14] Soysal T, Kou S. A simple test for solidification cracking susceptibility and filler metal effect[J]. Welding Journal, 2017, 96(10): 389s − 401s.
[15] Soysal T, Kou S. A simple test for assessing solidification cracking susceptibility and checking validity of susceptibility prediction[J]. Acta Materialia, 2018, 143: 181 − 197. doi: 10.1016/j.actamat.2017.09.065
[16] Savage W F, Lundin C D. The Varestraint test[J]. Welding Journal, 1965, 44(10): 433s − 442s.
[17] Liu K, Yu P, Kou S. Solidification cracking susceptibility of stainless steels: new test and explanation[J]. Welding Journal, 2020, 99(10): 255s − 270s. doi: 10.29391/2020.99.024
[18] Adamiec J. Evaluation of susceptibility of the ZRE1 alloy to hot cracking in conditions of forced strain[J]. Archives of Foundry Engineering, 2010, 10(1): 345 − 350.
[19] Huang C J, Cheng C M, Chou C P, et al. Hot cracking in AZ31 and AZ61 magnesium alloy[J]. Journal of Materials Science & Technology, 2011, 27(7): 633 − 640.
[20] Kierzek A, Adamiec J. Evaluation of susceptibility to hot cracking of magnesium alloy joints in variable stiffness condition[J]. Archives of Metallurgy and Materials, 2011, 56(3): 759 − 767.
[21] Liu L M, Dong C. Gas tungsten-arc filler welding of AZ31 magnesium alloy[J]. Materials letters, 2006, 60(17-18): 2194 − 2197. doi: 10.1016/j.matlet.2005.12.120
[22] Cao G P, Haygood I, Kou S. Onset of hot tearing in ternary Mg-Al-Sr alloy castings[J]. Metallurgical and Materials Transactions A, 2010, 41(8): 2139 − 2150. doi: 10.1007/s11661-010-0248-9
[23] Cao G P, Kou S. Hot tearing of ternary Mg-Al-Ca alloy castings[J]. Metallurgical and Materials Transactions A, 2006, 37(12): 3647 − 3663. doi: 10.1007/s11661-006-1059-x
[24] Cao G P, Kou S. Real-time monitoring of hot tearing in AZ91E magnesium casting[J]. Transactions of the American Foundry Society, 2007, 115: 7 − 34.
[25] Sun D X, Cui D L, Shi J T. Hot cracking and microstructure of welding joint of magnesium alloy AZ91D[J]. Advanced Materials Research, 2013, 753-755: 435 − 438. doi: 10.4028/www.scientific.net/AMR.753-755.435
[26] Zhou W, Long T Z, Mark C K. Hot cracking in tungsten inert gas welding of magnesium alloy AZ91D[J]. Materials Science and Technology, 2007, 23(11): 1294 − 1299. doi: 10.1179/174328407X213026
[27] Lang B, Sun D Q, Xuan Z Z, et al. Hot cracking of resistance spot welded magnesium alloy[J]. ISIJ International, 2008, 48(1): 77 − 82. doi: 10.2355/isijinternational.48.77
[28] Yu Z H, Yan H G, Chen S J, et al. Method for welding highly crack susceptible magnesium alloy ZK60[J]. Science and Technology of Welding and Joining, 2010, 15(5): 354 − 360. doi: 10.1179/136217110X12717725779661
[29] 魏子淇, 刘正, 王志, 等. 钇对Mg-Zn-Y-Zr合金热裂敏感性影响[J]. 中国有色金属学报, 2018, 28(2): 233 − 240. doi: 10.19476/j.ysxb.1004.0609.2018.02.03 Wei Ziqi, Liu Zheng, Wang Zhi, et al. Effects of Y on hot tearing susceptibility of Mg-Zn-Y-Zr alloys[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(2): 233 − 240. doi: 10.19476/j.ysxb.1004.0609.2018.02.03
[30] 伍迪灿, 王云峰, 杜文博, 等. Mg-xGd-1Er-0.5Zr合金热裂敏感性研究[J]. 中国有色金属学报, 2022, 32(2): 375 − 385. Wu Dichan, Wang Yunfeng, Du Wenbo, et al. Investigations on hot cracking susceptibility of Mg-xGd-1Er-0.5Zr alloys[J]. The Chinese Journal of Nonferrous Metals, 2022, 32(2): 375 − 385.
[31] Flemings M C. Solidification processing[M]. New York: McGraw-Hill, 1974.
计量
- 文章访问数: 295
- HTML全文浏览量: 81
- PDF下载量: 127
