Influence of tungsten electrode geometric characteristics on the thermodynamics behavior of arc and molten pool
-
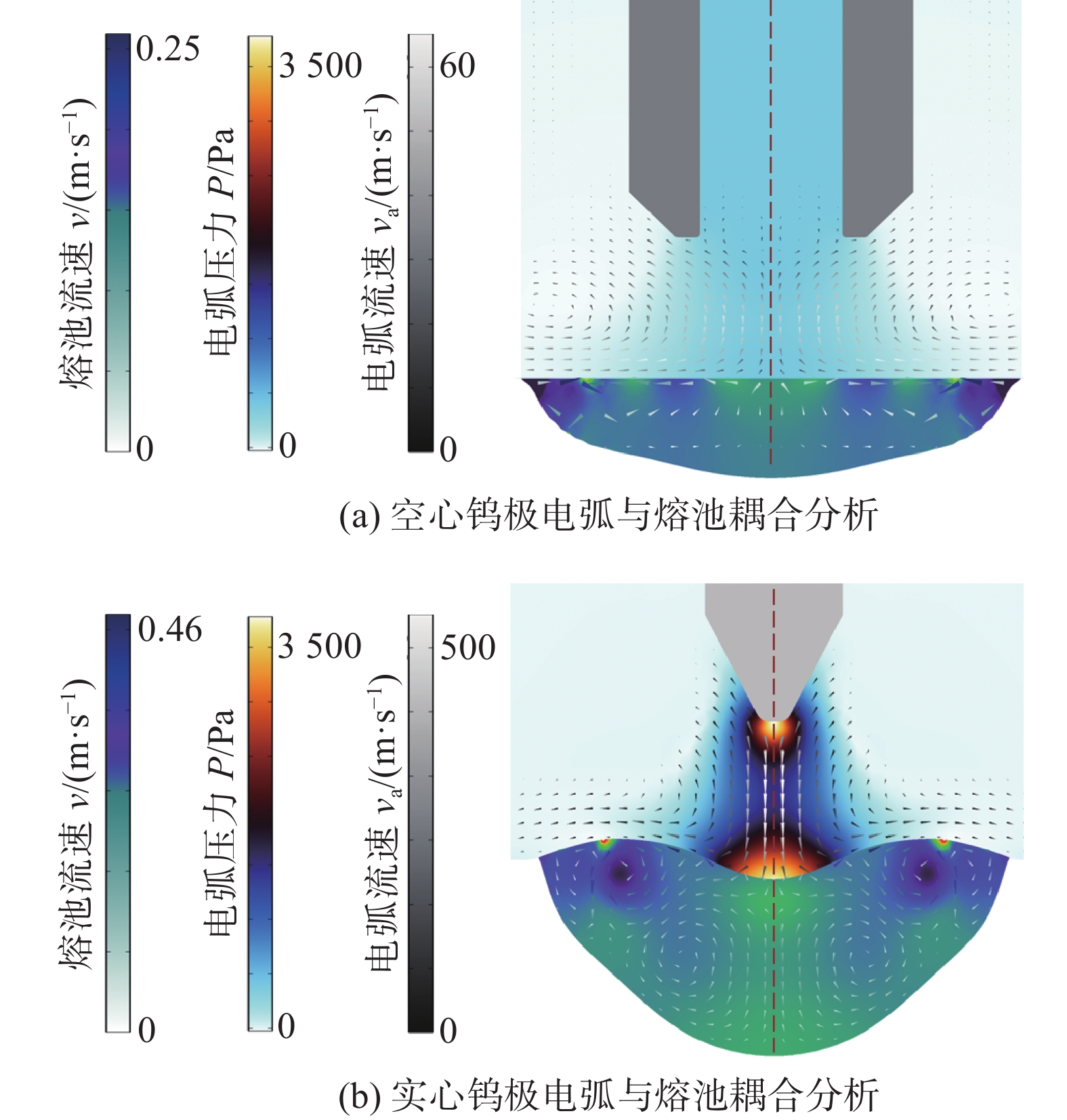
摘要: 电弧热力行为是影响液态金属流动，调控焊接质量的关键要素.利用高速摄像与数值模拟相结合的研究方法，系统分析了空心钨极与实心两种电极特征对电弧热力分布特征的影响.结果表明，焊接电流为350 A时，实心钨极焊缝呈现出深而窄的焊缝成形特征，空心钨极焊缝呈现出浅而宽的焊缝成形特征；距试板表面1 mm，实心钨极与空心钨极电弧沿水平方向的温度场和压力场均呈典型高斯分布特征，中心位置处空心钨极电弧的温度值和压力值分别为实心钨极的61.9%和23.5%；中轴线上实心钨极电弧压力分布呈U形特征，空心钨极电弧压力分布呈N形特征；构建的电弧与熔池强耦合分析模型与实际情况之间具有较好的一致性，可实现对电弧和熔池热力行为的分析与预测.Abstract: The thermodynamics behavior of arc is a key factor affecting the flow of molten pool and welding quality. High-speed photography and numerical simulation were used to systematically analyze the influence of the characteristics of hollow tungsten electrode and solid electrode on the thermal distribution characteristics of arc. The results showed that when the welding current was 350 A, the solid tungsten electrode weld exhibited deep and narrow weld formation characteristics, while the hollow tungsten electrode weld exhibited shallow and wide weld formation characteristics. At a distance of 1 mm from the surface of the test plate, both the temperature and pressure fields along the horizontal direction of the solid tungsten electrode and the hollow tungsten electrode arc exhibit typical Gaussian distribution characteristics, and the temperature and pressure values of the hollow tungsten electrode arc at the center position are 61.9% and 23.5% of those of the solid tungsten electrode, respectively. The pressure distribution of solid tungsten electrode arc on the central axis is U-shaped, while the pressure distribution of hollow tungsten electrode arc is N-shaped. The constructed strong coupling analysis model for arc and molten pool has good consistency with the actual situation, which can used to analyze and forecast the thermodynamics behavior of arc and molten pool.
-
0. 序言
纤维石英增强的二氧化硅复合材料(SiO2f/SiO2)具备热稳定性好、介电常数低、透波性能好和强度高等优点，广泛应用在导弹、卫星和火箭上[1]. 在SiO2f/SiO2复合材料的应用过程中，经常涉及到与自身或者其它金属的焊接，而钎焊是一种最常用的连接方法[2]. 由于SiO2f/SiO2复合材料的表面能很低，普通钎料对SiO2f/SiO2复合材料表面的润湿性很差，通常通过在钎料中添加活性元素来提高润湿性，AgCuTi是钎焊复合材料常用的活性钎料[3]，其中Ti元素由于活性高，能够与SiO2发生反应，降低界面能从而促进润湿[4]. Ti和SiO2的界面反应比较复杂.使用AgCuTi钎料钎焊SiO2材料时，界面结构为SiO2/TiSi2+Ti4O7[5]. 而使用AgCuInTi钎料钎焊SiO2f/SiO2复合材料时，界面结构为SiO2/TiO+TiSi2化合物[6].
在AgCuTi钎料和SiO2f/SiO2复合材料界面均发现了Ti-O和Ti-Si化合物，但是真正与SiO2结合的是哪种化合物并不清楚. 活性元素Ti在什么条件下与O反应，在什么条件下与Si发生反应，界面的反应机制也不清楚. 使用第一性原理计算能够从原子和电子的尺度研究界面原子的结合和反应机理. 因此，文中使用第一性原理计算深入研究了Ti和SiO2的界面结合机制.
1. 计算步骤与方法
使用第一性原理计算软件Materials Studio的CASTEP模块进行界面结合机理的研究，该软件基于密度泛函理论，采用赝势平面波方法进行计算. 经过收敛性测试，交换关联能采用GGA-PBE，截断能设置为340 eV，K点网格设置为3 × 6 × 1. 结构弛豫时，最大力、最大应力和最大位移的收敛阈值分别为0.5 eV/nm，0.1 GPa和 0.2e−3 nm.
为了验证选择的计算参数能够满足计算精度要求，对Ti的晶格进行了几何优化，驰豫后Ti的晶格参数为a = b = 0.295 92 nm，c = 0.465 57 nm，与试验结果(a = b = 0.295 06 nm，c = 0.467 88 nm)和其它文献[7]中的计算结果均比较接近，证明了计算参数选择的合理性.
对于Ti/SiO2界面，根据构建界面的最小错配度原则，建立了(3 × 1)Ti(10-10)/(31/2 × 1)SiO2(0001)界面模型，(3 × 1)Ti(10-10)层的晶格参数为：a = 0.467 88 nm，b = 0.885 18 nm，α = 90°，而 (31/2 × 1) SiO2 层的晶格参数为：a = 0.491 00 nm，b = 0.850 44 nm，α = 90°. 选用二者的平均数作为界面层的晶格参数. 对于构建好的界面模型，〈001〉方向上的错配度为2.35%，〈010〉方向上的错配度为1.96%. 根据表面能收敛性测试，建立了6层Ti(10 - 10)/16层SiO2 (0001)界面模型. 在z轴方向上加入了厚度为1.6 nm的真空层来分离两个表面层的自由表面.
对于SiO2 (0001)表面，既有可能是O终止表面，也有可能是Si终止表面，因此，分别建立了O终止面界面(O-T)和Si终止面界面(Si-T)模型，如图1所示. 在O-T界面中，Si和O原子比为1∶2.4，是一种富O界面；在Si-T界面中，Si和O原子比为1∶1.67，是一种富Si界面. 同时，对于同一种终止面界面，建立了三种典型的对位模型：Ti原子位于O原子的正上方(top)，Ti原子位于两个O原子的桥位的上方(bridge)，Ti原子位于三个O原子的空位的上方(hollow)，分别如图1c，1d，1e所示.
![]()
图 1 Ti/SiO2界面结构侧视图和三种不同界面结构俯视图Figure 1. Side view of Ti/SiO2 interfacial structure and three interface configurations. (a) O termination surface；(b) Si termination surface；(c) top；(d) bridge； (e) hollow2. 结果与讨论
2.1 不同界面结构的分离功
使用分离功(work of separation, Wsep)来评价Ti/SiO2界面结合的强度. 通常，分离功定义为把一个界面可逆地分成两个自由表面所需的功，可以由式(1)计算得出[8]，即
$$ {W_{{\rm{sep}}}} = \left( {{E_{{\rm{Si}}{{\rm{O}}_2}}} + {E_{{\rm{Ti}}}} - {E_{{\rm{interface}}}}} \right)/{A_{{\rm{interface}}}} $$ (1) 式中：
$E_{\rm {SiO}_2}$ ，ETi是单独的SiO2和Ti层的能量；Einterface是界面结构的总能量；Ainterface是界面的面积. 分离功可以用结合能关系(universal binding energy relation，UBER)[9]的方法进行计算，在UBER方法中，手动地将界面距离由一个很大的值逐渐调小，直至分离功达到最大然后变小，这样就可以得到最大的分离功和对应的平衡界面距离(d0). 然后，对分离功最大的界面结构进行驰豫，得到驰豫后的分离功.在驰豫过程中，仅对界面上下各三层原子进行驰豫，其余原子的位置保持固定不变.图2为不同Ti/SiO2界面结构的UBER曲线，曲线的峰值对应每种界面结构的最大分离功. 结果显示SiO2表面的终止面以及界面原子对位对界面结合强度均有影响. 总体来说，O终止面界面的分离功大于Si终止面界面的分离功，同时，相应的界面平衡距离也更短，表明界面形成的Ti-O键比Ti-Si键更强且键长更短. 对于O终止面界面，hollow对位界面的分离功最大为7.48 J/m2，界面平衡距离为0.12 nm. 而top和bridge对位界面的分离功分别为6.24 J/m2和7.07 J/m2. 对于Si终止面界面，不同的对位对界面分离功影响较小，top和bridge对位界面的UBER曲线基本重合，最大分离功为2.24 J/m2，界面平衡距离为0.20 nm，而hollow对位界面的分离功为1.97 J/m2.
图3为驰豫后的Ti/SiO2界面结构侧视图，其中图3a为O终止面hollow对位界面驰豫以后的界面结构，驰豫后界面的分离功为8.99 J/m2，大于未驰豫的界面分离功. 在弛豫过程中，界面处的Ti原子和O原子逐渐向对方运动. 同时发现，次界面层的Ti原子也运动到界面与O成键，表明O对Ti有很强的的吸引力. 界面的Ti-O键长由驰豫前的0.238 2 nm缩短到0.201 2 ~ 0.206 3 nm，这已经与TiO2体相内Ti-O键长(0.197 3 nm)极为接近. 图3b为Si终止面hollow对位界面驰豫以后的界面结构，驰豫后界面的分离功为2.65 J/m2，同样也大于未弛豫的界面分离功. 弛豫后界面的Ti-Si键长0.246 7 ~ 0.253 1 nm，略大于驰豫前键长(0.242 3 ~ 0.247 3 nm). 而TiSi2化合物中的Ti-Si键长为0.274 1 nm.
![]()
图 3 驰豫后的Ti/SiO2界面结构侧视图Figure 3. Side view of relaxed Ti/SiO2 interfacial structure. (a) O termination surface; (b) Si termination surface2.2 电子行为
原子间的键合强度决定了界面的力学性能，因此，进一步研究了Ti/SiO2界面的电子行为.
图4为驰豫后界面的差分电荷密度图，其中图4a为O终止界面的差分电荷密度图，差分密度图是由整个界面的电子密度减去每个原子初始的电子密度得到的. 可以看出，界面处的O原子周围有电荷聚集区，而Ti原子周围有电荷大耗散区，表明O原子和Ti原子分别得到和失去电子，变为负离子和正离子，并通过静电引力形成离子键. 使用Mulliken布居数半定量地评价了电荷转移和离子性，结果显示Ti1和O1 原子的布居数分别为+0.24 和−0.91，界面Ti1-O1的键集居数为0.29，表明界面形成的Ti-O键主要是离子键. 图4b为Si终止面界面的差分电荷密度图，界面处的Ti2和Si2原子周围均有电荷的耗散区，说明两个原子均失去电子，两个原子间的区域有电荷的聚集区，说明电子归两个原子共有，键合有共价键的成分. Ti2和Si2原子的布居数分别为−0.27和+1.04，说明界面的Ti和Si原子之间也有电荷转移，键合有离子键的成分，Ti2-Si2键的键集居数为0.76，说明界面的Ti-Si键的离子键成分较小，共价键的成分较大.
![]()
图 4 驰豫后界面的差分电荷密度图Figure 4. Charge density difference for the interface after relaxation. (a) O termination surface; (b) Si termination surface图5为驰豫后界面特定原子的分态密度图(partial density of stats，PDOS)，其中图5a为O终止界面的PDOS，可以发现Ti和O原子的态密度在−11.5 ~ +1.3 eV的能量范围内有明显的重叠，对应Ti-3d/O-2p电子的强烈杂化，表明原子之间的离子键结合. 同时，Ti的p和d轨道在−22.5 ~ −19.3 eV的能量范围出现了很小的峰，与O-s轨道电子态密度的峰在同一位置，这个位置的峰宽度较窄，表明电子局域化程度较高，界面的Ti-O键还有小部分共价键的成分. 图5b为Si终止面界面部分原子的态密度图，在−11 ~ +1 eV能量区域，Si和Ti有范围较大的峰的重合，表明之间的键合有离子键的成分. 在−3 ~ +1 eV能量范围内，有重合度很高，宽度很窄的峰，表明键合有共价键的成分，说明界面形成的Ti-Si键是共价-离子混合键.
![]()
图 5 驰豫后界面特定原子的PDOSFigure 5. PDOS projected on selected atoms of interface after relaxation. (a) O termination surface; (b) Si termination surface2.3 界面能
界面能(γ)可以用来评价特定条件下界面结构的热力学稳定性，界面能可以由下式计算得到[10]
$$ \gamma = \dfrac{1}{{2A}}\left( {{G_{{\rm{slab}}}} - N_{\rm{O}}^{}\mu _{\rm{O}}^{} - N_{{\rm{Si}}}^{}\mu _{{\rm{Si}}}^{} - {N_{{\rm{Ti}}}}\mu _{{\rm{Ti}}}^{}} \right)= \dfrac{1}{{2A}}\left[ {{G_{{\rm{slab}}}} - \dfrac{1}{2}N_{\rm{O}}^{}\mu _{{\rm{Si}}{{\rm{O}}_2}}^0 - \left( {N_{{\rm{Si}}}^{} - \dfrac{1}{2}N_{\rm{O}}^{}} \right)\mu _{{\rm{Si}}}^{} - {N_{{\rm{Ti}}}}\mu^0 _{{\rm{Ti}}}} \right] $$ (2) 式中：Gslab是界面的吉布斯自由能；Ni和μi分别是i(i = Si, O, Ti, SiO2)原子的数量和化学势.
考虑到温度的影响，Si的化学势可以表示为
$$\mu _{{\rm{Si}}}^{} = \mu _{{\rm{Si}}}^0 + kT\ln {a_{{\rm{Si}}}}$$ (3) 式中：k是玻尔兹曼常数；T是温度；aSi是Si的活度. 因此，界面能可以进一步表示为
$$\gamma = \frac{1}{{2A}}\Biggr[ {E_{{\rm{slab}}}} - \frac{1}{2}N_{\rm{O}}^{}\mu _{{\rm{Si}}{{\rm{O}}_2}}^0 - \left( {N_{{\rm{Si}}}^{} - \frac{1}{2}N_{\rm{O}}^{}} \right)\left( {\mu _{{\rm{Si}}}^0 + kT\ln {a_{{\rm{Si}}}}} \right) -{N_{{\rm{Ti}}}}\mu _{{\rm{Ti}}}^{\rm{0}} \Biggr]$$ (4) SiO2的表面既有可能是O终止面，也有可能是Si终止面. 根据之前的结算结果，如果O终止面界面稳定，界面会形成Ti-O化合物；如果Si终止面界面稳定，界面会形成Ti-Si化合物. 图6为Ti/SiO2界面在1 173 K时的不同界面结构的界面能. 对于富Si界面，界面能随着Si活度的下降而上升，而富O界面显示出相反的趋势. 当Si的活度大于e−35时，富Si界面稳定，Si的活度小于e−35时，富O界面稳定. 因此，在使用含Ti钎料钎焊SiO2时，界面处易形成Ti-O化合物，反应式如下
$$ {\rm{Ti}} + {\rm{Si}}{{\rm{O}}_2} \to {\rm{Ti}} {\text{-}} {\rm{O}} + {\rm{Si}} $$ (5) SiO2中的Si就被Ti置换出来. Si扩散进入钎料后，活度升高，与钎料中的Ti反应生成Ti-Si化合物，即
$$ {\rm{Ti}} + {\rm{Si}} \to {\rm{Ti}} {\text{-}} {\rm{Si}} $$ (6) 界面应该为SiO2/Ti-O化合物/Ti-Si化合物/钎料.
3. 结论
(1)建立了错配度很小的Ti(10-10)/SiO2(0001)界面模型，分别考虑了不同的终止面和原子对位. 结果发现，O终止面界面的分离功大于Si终止面界面的分离功，同时，相应的界面平衡距离也更短，对于O终止面界面，驰豫后分离功最大为8.99 J/m2，Si终止面界面为2.65 J/m2.
(2)使用差分电荷密度、Mulliken布局数和态密度研究了界面电子行为，发现在O终止面界面，Ti和O原子之间形成很强的离子-共价键；而在Si终止面界面，Ti和Si之间形成的键合主要是共价键，也有部分离子键的成分.
(3)在钎焊温度1 173 K下，当Si的活度大于e−35时，富Si界面稳定，Si的活度小于e−35时，富O界面稳定. 在使用含Ti钎料钎焊SiO2f/SiO2复合材料时，界面处易形成Ti-O化合物. SiO2中的Si被Ti置换出来. Si扩散进入钎料后，活度升高，与钎料中的Ti反应生成Ti-Si化合物，所以界面应该为SiO2/Ti-O化合物/Ti-Si化合物/钎料.
-
![]()
图 2 空心钨极与实心钨极焊缝成形对比
Figure 2. Comparison of weld formation between hollow tungsten electrode and solid tungsten electrode. (a) weld morphology of hollow tungsten electrode; (b) weld morphology of solid tungsten electrode
![]()
图 3 空心钨极与实心钨极电弧及熔池特性对比
Figure 3. Arc and molten pool characteristics comparison between hollow tungsten electrode and solid tungsten electrode. (a) hollow tungsten electrode; (b) solid tungsten electrode
![]()
图 5 中轴线电弧温度场分布特征
Figure 5. Distribution characteristics of arc temperature field along the central axis
![]()
图 6 距试板表面1.0 mm电弧温度场分布特征
Figure 6. Distribution characteristics of arc temperature field at 1.0 mm from the surface of molten pool
![]()
图 7 中轴线电弧压力场分布特征
Figure 7. Distribution characteristics of arc pressure field along the central axis
![]()
图 8 距试板表面1.0 mm电弧压力分布特征
Figure 8. Characteristics of arc pressure distribution at 1.0 mm from the surface of molten pool
表 1 电弧形貌及熔池特征
Table 1 Arc morphology and molten pool characteristics
钨极类型 电弧实际形貌 电弧形貌示意图 熔池特征 电弧形貌示意图 实心钨极 
空心钨极 
下载: 导出CSV
-
[1] Esme U, Bayramoglu M, Kazancoglu Y, et al. Optimization of weld bead geometry in TIG welding process using grey relation analysis and Taguchi method[J]. Materials and Technologies, 2009, 43(3): 143 − 149.
[2] 马壮, 张莉, 王义伟. 有色合金A-TIG焊研究现状[J]. 材料导报, 2014, 28(1): 91 − 94. Ma Zhuang, Zhang Li, Wang Yiwei. Research status of A-TIG welding for Non-ferrous alloy[J]. Materials Reports, 2014, 28(1): 91 − 94.
[3] Lidsky L M, Rothleder S D, Rose D J, et al. Highly ionized hollow cathode discharge[J]. Journal of Applied Physics, 1962, 33(8): 2490 − 2497. doi: 10.1063/1.1729002
[4] Tashiro S, Tanaka M, Nakatani M, et al. Numerical analysis of energy source properties of hollow cathode arc[J]. Surface and Coatings Technology, 2007, 201(9-11): 5431 − 5434. doi: 10.1016/j.surfcoat.2006.07.158
[5] 杨义成, 陈健, 黄瑞生, 等. 空心钨极焊接关键技术问题及发展现状[J]. 焊接, 2021(5): 1 − 8. Yang Yicheng, Chen Jian, Huang Ruisheng et al. Key technical problem and development status of hollow tungsten arc welding[J]. Welding & Joining, 2021(5): 1 − 8.
[6] 杨义成, 杜兵, 黄继华, 等. 空心钨极同轴填丝焊空间热场分布特征[J]. 焊接学报, 2022, 43(3): 63 − 67. doi: 10.12073/j.hjxb.20210908001 Yang Yicheng, Du Bing, Huang Jihua, et al. Spatial thermal field distribution characteristics of hollow cathode arc welding with coaxial filler wire[J]. Transactions of the China Welding Institution, 2022, 43(3): 63 − 67. doi: 10.12073/j.hjxb.20210908001
[7] 杨义成, 杜兵, 黄继华, 等. 空心钨极同轴填丝焊接丝弧交互作用机制[J]. 焊接学报, 2022, 43(4): 94 − 99. Yang Yicheng, Du Bing, Huang Jihua, et al. Mechanism of wire and arc interaction in hollow tungsten arc welding with coaxial filler wire[J]. Transactions of the Chin Welding Institution, 2022, 43(4): 94 − 99.
[8] Cho D W, Lee S H, Na S J. Characterization of welding arc and weld pool formation in vacuum gas hollow tungsten arc welding[J]. Journal of Materials Processing Technology, 2013, 213(2): 143 − 152. doi: 10.1016/j.jmatprotec.2012.09.024
[9] Chen S, Yan Z, Jiang F, et al. The pressure distribution of hollow cathode centered negative pressure arc[J]. Journal of Manufacturing Processes, 2016, 23: 21 − 28. doi: 10.1016/j.jmapro.2016.05.016
[10] 陈树君, 盛珊, 蒋凡, 等. 空心钨极中心负压电弧的物理性能[J]. 焊接学报, 2017, 38(12): 1 − 4. doi: 10.12073/j.hjxb.20171230 Chen Shujun, Sheng Shan, Jiang Fan, et al. Physical properties of hollow tungsten central negative pres sure arc[J]. Transactions of the China Welding Institution, 2017, 38(12): 1 − 4. doi: 10.12073/j.hjxb.20171230
[11] 陈树君, 王建新, 蒋凡, 等. 空心钨极中心负压电弧基础特性研究[J]. 机械工程学报, 2016, 52(2): 7 − 12. doi: 10.3901/JME.2016.02.007 Chen Shujun, Wang Jianxin, Jiang Fan, et al. Research of hollow tungsten central negative pressure arc welding characteristic[J]. Journal of Mechanical Engineering, 2016, 52(2): 7 − 12. doi: 10.3901/JME.2016.02.007
[12] Jiang F, Yan Z, Chen S, et al. The energy distribution of electrode in hollow cathode centered negative pressure arc[J]. Journal of Manufacturing Processes, 2016, 24: 138 − 144. doi: 10.1016/j.jmapro.2016.08.005
-
期刊类型引用(1)
1. 陆益敏，马丽芳，王海，奚琳，徐曼曼，杨春来. 脉冲激光沉积技术生长铜材碳基保护膜. 材料研究学报. 2023(09): 706-712 . 
百度学术
其他类型引用(1)
计量
- 文章访问数: 171
- HTML全文浏览量: 20
- PDF下载量: 50
- 被引次数: 2
