Numerical simulation of the effect of wire feeding speed on the molten pool flow and weld bead morphology of WAAM
-
摘要: 通过数值模拟研究了不同送丝速度下电弧增材制造单道熔积成形过程中的传热传质及熔池流态，分析了送丝速度对焊道形貌的影响. 结果表明，当送丝速度较小时，基板接受的电弧热较多，熔池的熔深较深且流动性较强，成形焊道较宽且高度较低；随着送丝速度的增大，熔融金属向上堆积，熔池体积增加，送丝速度达到一定值时，电磁力与表面张力达到动态平衡，熔深与焊道高度接近；当送丝速度较大时，液态金属对流减弱，熔深较浅，在表面张力的作用下，熔池边缘收缩导致焊道隆起. 模拟与试验结果吻合较好，研究结果可以为GTAW电弧增材技术的工艺参数调控提供理论依据.Abstract: The heat and mass transfer and molten pool flow in single-pass deposition of wire arc additive manufacturing (WAAM) were studied using numerical simulation, and the influence of wire feeding speed on weld bead morphology was analyzed. The results show that when the wire feeding speed is low, the substrate receives more arc heat, the molten pool has deeper penetration and stronger fluidity, and the weld bead width is wide with a low height. As the wire feeding speed increases, the molten metal accumulates upward, and the molten pool volume increases. When the wire feeding speed reaches a certain value, the electromagnetic force and surface tension achieve a dynamic balance, and the molten pool penetration approaches the weld bead height. At higher wire feed speeds, molten pool convection tends to weaken, and penetration becomes shallow. Under the action of surface tension, edge shrinkage of the weld pool leads to weld bead bumps. The simulated single-bead cross-sectional profile agrees well with experimental results and can provide theoretical bases for controlling process parameters in gas tungsten arc welding-based additive manufacturing technology.
-
0. 序言
老化和腐蚀问题影响着长输管线的安全运行，在役焊接修复技术可以在保证管道不停输的情况下对其进行修复，是一种安全、高效、环保的管道修复技术[1-3].
然而，烧穿是在役焊接面临的主要问题，在过去三十多年中，国内外学者针对烧穿问题进行了许多研究，美国BWI研究所对烧穿预测进行了相关研究，并提出了内壁温度982℃为烧穿的临界温度[4]. Cisilino等人[5]从壁厚的角度研究烧穿问题，并指出壁厚6.4 mm为烧穿的临界壁厚. Boring等人[6]提出径向变形量0.38 mm为临界变形量. 郭广飞[7]从剩余强度的角度预测烧穿，并研究了温度、压力、壁厚和管径等因素对剩余强度的影响规律. Wu等人[8]对剩余强度法进行了优化，并建立了热输入与积分温度下限的线性表达式. Majnoun等人[9]通过引入“剩余厚度”这一临界参数，建立了一种新的热力学判据预测烧穿. 目前，国内外学者对在役焊接烧穿预测的研究仅仅考虑烧穿瞬间各项指标，而不能有效地基于理论将烧穿量化，缺乏对烧穿过程演化的分析.
连续介质损伤力学的发展为研究在役焊接烧穿过程提供了新思路. Lemaitre[10]基于连续损伤力学建立了损伤与累计塑性应变的线性表达式，用于预测金属的韧性开裂. Oyane[11]考虑了静水应力对韧性断裂的影响，并建立了相关断裂准则. Bonora等人[12-13]在Lemaitre准则的基础上，考虑了初始损伤阈值应变、临界损伤断裂应变、临界损伤值对金属形变过程中损伤演化的影响. 杨超众[14]基于Bonaro模型，建立了316LN钢的高温损伤演化方程，并通过试验验证了该方程能够较好地预测该材料的热成形开裂问题.
试验采用数学建模、有限元模拟和试验相结合的方式，构建在役焊接过程中的高温损伤演化方程，研究在役焊接过程中的损伤演化规律，分析不同因素对损伤演化的影响规律.
1. 试验方法
1.1 高温拉伸试验
在役焊接过程中，熔池下方金属的形变行为与其高温性能参数密切相关，因此研究在役焊接过程中的失效行为，有必要通过高温拉伸试验获得X70管线钢母材高温性能参数. 试验中设定温度分别为1 000，1 100，1 200，1 300 ℃. 根据前期在役焊接数值模拟结果，设定试样拉伸变形的应变速率为0.1/s和1.0/s.
试样在拉伸之前，需以10 ℃/s的速度加热到1 350 ℃，并在此温度下保温5 min，然后以相同的速度冷却到设定温度进行拉伸试验，获得的应力应变曲线如图1所示.
1.2 在役焊接试验
在役焊接所采用的试验装置如图2所示，为模拟实际在役焊接过程中管道的带压焊接，采用水泵和节流阀实现焊接工件夹具两端进水口和出水口介质流速的差异，从而实现焊接工件内部的带压，通过调节节流阀改变出水口的介质流量从而实现为焊接工件内部压力的不同.
焊接方式采用不填丝TIG焊，X70试管管径为114 mm，壁厚为4 mm，试验参数及烧穿情况如表1所示.
表 1 在役焊接试验相关工艺参数Table 1. Welding parameters of in-service welding序号 焊接电流 I/A 焊接电压 U/V 焊接速度 v/(mm·s−1) 热输入 Q/(J·mm−1) 压力 P/MPa 烧穿情况 1 255 13.7 4 870 6.5 未烧穿 2 260 13.8 4 890 6.5 未烧穿 3 265 13.7 4 910 6.5 未烧穿 4 270 13.8 4 930 6.5 未烧穿 5 275 13.9 4 955 6.5 未烧穿 6 280 14.0 4 980 6.5 烧穿 可以发现前5组试验均未发生烧穿，当热输入增大到980 J/mm时，发生烧穿失效.
2. BONARO模型数学建模
2.1 BONARO数学模型
在多轴加载中，Bonaro准则为
$$ D = {D_0} + \left( {{D_{{\rm{cr}}}} - {D_0}} \right)\left\{ {1 - {{\left[ {1 - \frac{{\ln \left( {{p \mathord{\left/ {\vphantom {p {{p_{{\rm{th}}}}}}} \right. } {{p_{{\rm{th}}}}}}} \right)}}{{\ln \left( {{{{\varepsilon _{{\rm{cr}}}}} \mathord{\left/ {\vphantom {{{\varepsilon _{{\rm{cr}}}}} {{\varepsilon _{{\rm{th}}} }}}} \right. } {{\varepsilon _{{\rm{th}}}}}}} \right)}}f\left( {\frac{{{\sigma _{\rm{m}}}}}{{\overline \sigma }}} \right)} \right]}^\alpha }} \right\} $$ (1) $$ f\left( {\frac{{{\sigma _{\rm{m}}}}}{{\overline \sigma }}} \right) = \frac{2}{3}\left( {1 + \nu } \right) + 3\left( {1 - 2\nu } \right){\left( {\frac{{{\sigma _{\rm{m}}}}}{{\overline \sigma }}} \right)^2} $$ (2) $$ {P_{{\text{cr}}}}{\text{ = }}{\varepsilon _{{\text{th}}}}{\left( {\frac{{{\varepsilon _{{\rm{cr}}}}}}{{{\varepsilon _{{\rm{th}}}}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 {f\left( {{{{\sigma _{\rm{m}}}} \mathord{\left/ {\vphantom {{{\sigma _m}} {\overline \sigma }}} \right. } {\overline \sigma }}} \right)}}} \right. } {f\left( {{{{\sigma _m}} \mathord{\left/ {\vphantom {{{\sigma _m}} {\overline \sigma }}} \right. } {\overline \sigma }}} \right)}}}} $$ (3) 式中：D表示材料累计损伤值；
$ {D}_{0} $ 表示初始损伤值；${D}_{{\rm{cr}}}$ 表示临界损伤值；P表示累计等效塑性应变；$ {P}_{{\rm{cr}}} $ 表示多轴应力状态下的临界损伤断裂应变；$ {P}_{{\rm{th}}} $ 表示多轴应力状态下初始损伤断裂应变；$ {\varepsilon }_{{\rm{th}}} $ 表示单轴应力状态下的初始损伤阈值应变；$ {\varepsilon }_{{\rm{cr}}} $ 表示单轴应力状态下的临界损伤断裂应变；$ \nu $ 表示泊松比；$ {\sigma }_{{\rm{m}}} /\stackrel{-}{\sigma } $ 表示应力三轴度；$ \alpha $ 表示损伤因子；$ {\sigma }_{{\rm{m}}} $ 表示等效应力；$ \stackrel{-}{\sigma } $ 表示静水应力.2.2 损伤模型参数的确定
使用Bonaro模型描述材料的高温失效行为需要5个材料参数：
$ {\varepsilon }_{{\rm{th}}} $ ，$ {\varepsilon }_{{\rm{cr}}} $ ，$ {D}_{{\rm{cr}}} $ ，$ {D}_{0} $ ，$ \alpha $ . 一般认为初始材料内部不存在损伤，即$ {D}_{0} $ = 0，对于钢类材料$ \alpha $ = 0.45 ~ 0.6，文中取$ \alpha $ = 0.5[15]，因此需要确定的材料参数仅剩$ {\varepsilon }_{{\rm{th}}} $ ，$ {\varepsilon }_{{\rm{cr}}} $ ，$ {D}_{{\rm{cr}}} $ .根据文献[16]所提方法，初始损伤阈值应变
$ {\varepsilon }_{{\rm{th}}} $ 可用载荷行程曲线最高点对应应变代替，临界损伤值可由如下公式计算$$ {D_{{\rm{cr}}} } = 1 - \frac{{{\sigma _{\rm{R}}}}}{{{\sigma _{\rm{u}}}}} $$ (4) 式中：
$ {\sigma }_{R} $ 表示断裂应力；$ {\sigma }_{u} $ 表示峰值应力.临界损伤断裂应变
$ {\varepsilon }_{{\rm{cr}}} $ 采用文献[14]所提方法进行确定，结果如表2所示.表 2 损伤模型参数结果Table 2. Damage model parameter results温度T/K 应变速率0.1/s 应变速率1.0/s 初始损伤阈值应变$ {\varepsilon }_{{\rm{th}}} $ 临界断裂应变$ {\varepsilon }_{{\rm{cr}}} $ 断裂应力$ {\sigma }_{{\rm{R}}} $/MPa 峰值应力$ {\sigma }_{{\rm{u}}} $/MPa 临界损伤值$ {D}_{{\rm{cr}}} $ 初始损伤阈值应变$ {\varepsilon }_{{\rm{th}}} $ 临界断裂应变$ {\varepsilon }_{{\rm{cr}}} $ 断裂应力$ {\sigma }_{{\rm{R}}} $/MPa 峰值应力$ {\sigma }_{{\rm{u}}} $/MPa 临界损伤值$ {D}_{{\rm{cr}}} $ 1 273 0.163 0.256 77.3 115.3 0.33 0.161 0.250 96.4 139.7 0.31 1 373 0.143 0.263 39.3 63.4 0.38 0.168 0.257 63.1 97.0 0.35 1 473 0.131 0.257 25.9 45.6 0.43 0.153 0.251 42.4 70.7 0.40 1 573 0.123 0.252 20.4 38.4 0.47 0.143 0.246 30.8 55.1 0.44 流变应力与温度和应变率的关系可以用Z参数表示为[17]
$$ Z=\stackrel{·}{\varepsilon }\mathrm{exp}\left(\frac{Q}{RT}\right) $$ (5) 式中：Z表示温度补偿速率因子；R表示气体常数；Q表示变形激活能.
试验主要通过Z参数建立
$ {\varepsilon }_{{\rm{th}}} $ 、$ {\varepsilon }_{{\rm{cr}}} $ 、$ {D}_{{\rm{cr}}} $ 与温度和应变率之间的关系式，材料高温形变过程中，可用Arrhenius方程的幂函数形式来描述流变应力与温度和应变率的关系为[18]$$ \stackrel{·}{\varepsilon }={A}_{1}{\sigma }^{{n}_{1}}\mathrm{exp}\left(-\frac{Q}{RT}\right) $$ (6) 式中：
$ {A}_{1} $ 表示材料常数；$ {n}_{1} $ 表示加工硬化指数.对材料参数进行数学建模前需确定X70管线钢的变形激活能Q，由公式(6)可以推导出变形激活能Q的表达式为
$$ Q=R{\left[\frac{\partial \mathrm{ln}\stackrel{·}{\varepsilon }}{\partial \mathrm{ln}{\sigma }_{{\rm{p}}}}\right]}_{T}{\left[\frac{\partial \mathrm{ln}{\sigma }_{{\rm{p}}}}{\partial \left(1/T\right)}\right]}_{\stackrel{·}{\varepsilon }} $$ (7) 根据表2，对不同温度、不同应变率下的峰值应力进行最小二乘法拟合，可以求得Q = 408.77 kJ/mol.
根据表2中的数据对
$ {\varepsilon }_{{\rm{th}}} $ ，$ {\varepsilon }_{{\rm{cr}}} $ ，$ {D}_{{\rm{cr}}} $ 进行数学建模，参照参数Z的表达式形式，分别采取应变速率的指数形式和温度倒数的指数形式作为自变量进行拟合，得到$ {\varepsilon }_{{\rm{th}}} $ ，$ {\varepsilon }_{{\rm{cr}}} $ ，$ {D}_{{\rm{cr}}} $ 与温度和应变速率的表达式，误差分别为1.62%、1.23%和0.5%. 结合Bonaro损伤模型，得到X70管线钢高温损伤演化方程.$$ \left\{\begin{array}{l} D=D_{{\rm{c r}}}\left\{1-\left[1-\ln \dfrac{\left(p / p_{{\rm{th}}}\right)}{\varepsilon_{{\rm{c r}}} / \varepsilon_{{\rm{th}}}} f\left(\dfrac{\sigma_{{\rm{m}}} }{\bar{\sigma}}\right)\right]^{0.5}\right. \\ \varepsilon_{{\rm{t h}}}=0.135 \varepsilon \exp \left(2.2891\left|\dfrac{1}{T}-\dfrac{1}{1723}\right|^{1.5} \dfrac{Q}{R}\right) \\ \varepsilon_{{\rm{c r}}}=0.257 \varepsilon^{-0.01065} \exp \left(-0.00935\left|\dfrac{1}{T}-\dfrac{1}{T_{c}}\right| \dfrac{Q}{R}\right) \\ D_{{\rm{c r}}}=1.996 \varepsilon^{-0.03} \exp \left(-0.0484 \dfrac{Q}{R T}\right) \\ p \varepsilon_{{\rm{c r}}} \cong \varepsilon_{{\rm{t h}}}\left(\dfrac{\varepsilon_{{\rm{c r}}}}{\varepsilon_{{\rm{t h}}}}\right)^{1 / f\left(\sigma_{{\rm{m}}} / \sigma\right)} \\ f\left(\dfrac{\sigma_{{\rm{m}}} }{\bar{\sigma}}\right)=\dfrac{2}{3}(1+v)+3(1-2 v)\left(\dfrac{\sigma_{{\rm{m}}} }{\bar{\sigma}}\right)^{2} \end{array}\right. $$ (8) 3. 在役焊接数值模拟
为了分析在役焊接过程中的损伤演化规律，在试验结束后，对在役焊接温度场和应力应变场进行数值模拟并耦合X70管线钢高温损伤演化方程.
基于试验管道的几何形状，建立三维有限元模型，为节约计算时间，焊接接头区域采用密集网格，而其他区域采用稀疏网格，通过前期网格敏感性计算，建立如图3所示半管模型，最大网格尺寸为2 mm × 5 mm × 6 mm，最小网格尺寸为0.25 mm × 0.5 mm × 0.35 mm.
![]()
图 3 管道模型Figure 3. Model of the pipeline. (a) 3D model of half pipeline; (b) 2D model of welded joint采用Goldak等人[19]提出的双椭球热源进行数值模拟，该热源模型充分考虑了电弧能量非对称分布的特点，广泛应用于电弧焊的数值模拟中；依据试验管道内压情况和装卡情况，对管道模型内壁施加垂直于模型内表面指向外的均匀压力，对管道模型两端施加刚性约束.
在役焊接过程管道外表面与空气的换热方式主要有自然对流和辐射；对于工件内表面，则必须考虑内壁与介质的强制对流，在试验中，外壁换热系数取29 W/(m2·℃)，内壁换热系数取1 800 W/(m2·℃)[20].
4. 结果和分析
4.1 损伤演化过程分析
根据试验结果分析可知，当热输入由955 J/mm增达到980 J/mm时，发生烧穿失效，因此选取这2组试验参数进行分析. 为方便对在役焊接过程中熔池下方区域损伤值进行分析，规定热源正下方-熔深最大处-熔池末端的取点路径，如图4所示.
首先对热输入为955 J/mm时的损伤请况进行分析，图5a和图5b分别为5.75 s时路径B1至X8内壁点和路径X4上熔合线至内壁的损伤值的分布图，可以看出损伤在热源正下方靠后的位置才开始积累，最大损伤值出现在熔深最大处后方的位置，且壁厚方向上，损伤值由熔合线向内壁逐渐减小.
![]()
图 5 不同路径损伤分布Figure 5. Distribution of damage values in differnet paths. (a) Path from B1 to X8; (b) Path X4 from weld line to the inner wall图6展示了路径X4由熔合线至内壁方向上各节点的损伤值随时间的变化请况，可以看出，4.75 s时，各节点损伤值均为0，5 s时，熔合线附近节点出现损伤，并随时间逐渐增大，且在任意时刻下，熔合线处损伤值均大于内壁处，这说明在役焊接过程中，熔合线位置更容易萌生损伤.
接下来对热输入980 J/mm的损伤分布请况进行分析，图7展示了路径X1至X5方向上内壁节点在5 ~ 6 s时间段内的损伤演变请况，可以看出内壁上最大损伤值出现在熔深最大处后方1.4 ~ 1.8 mm区域内，路径X2至X5内壁节点损伤值在5.75 s和6 s时相同，这说明损伤值并不会无限增大，且从时间角度来看，最大熔深处后方1.4 mm位置的损伤值最先达到最大值. 图8a和图8b分别为5.5 s和5.75 s路径X1至X5内壁节点损伤值与临界损伤值的对比图，可以看出，5.5 s时内壁节点损伤值均小于其对应的临界损伤值，即未发生烧穿失效；而5.75 s时X2，X3，X4内壁节点的损伤值达到其对应的临界损伤值，即这些位置发生失效，这与试验过程中第6组发生烧穿的情况相吻合，同时，发生失效的节点位于最大熔深处后方1 ~ 2 mm区域内，这与文献[21]中结论相符，这说明所建立的X70高温损伤演化方程能够较好地预测在役焊接过程中的损伤演化情况.
![]()
图 8 损伤值与临界损伤值的对比Figure 8. Comparison of damage and critical value. (a) 5.5 s; (b) 5.75 s4.2 管道内压对在役焊接损伤演化的影响
在保证在役焊接热输入980 J/mm、管道壁厚4 mm的情况下，进行不同管道内压(1.5，2.5，3.5，4.5，5.5，6.5 MPa)下的在役焊接数值模拟，并耦合所建立的损伤演化方程.
图9展示了不同内压下5.75 s时路径B1至X8内壁节点的损伤值分布情况，可以看出，内壁损伤值随内压的增大而增加；图10展示了5.75 s路径X4上节点损伤值分布情况，可以看出，不同内压下，由熔合线至内壁的损伤分布趋势基本一致，均由熔合线至内壁递减，当管道内压为1.5 MPa时，路径节点损伤值均为0，这说明损伤萌生存在临界内压.
![]()
图 9 不同压力下的损伤分布(B1-X8)Figure 9. Distribution of damage values at different pressure (B1-X8)从累计塑性应变P和临界损伤断裂应变
$ {P}_{{\rm{cr}}} $ 的角度解释压力对在役焊接损伤失效的影响，图11展示了路径X4上内壁节点的累计塑性应变和临界损伤断裂应变随内压的变化请况，通过分析可知，随着管道内压的增大，内壁累计塑性应变逐渐增大，临界损伤断裂应变则逐渐减小，且管道内压的变化对累计塑性应变的影响幅度更大，当内压达到6.5 MPa时，累计塑性应变等于临界损伤断裂应变，内壁发生损伤失效，这说明在役焊接过程中，管道内压越大，烧穿失效的风险更高.4.3 壁厚对在役焊接损伤演化的影响
在保证焊接热输入980 J/mm、管内介质压力6.5 MPa的情况下，采用不同壁厚(4.0 mm、4.2 mm、4.4 mm、4.6 mm)的管道模型进行在役焊接数值模拟，并耦合缩得到的损伤演化方程.
图12为不同管道壁厚下路径B1至路径X8内壁节点的损伤分布图，可以看出，随着管道壁厚的增加，内壁内壁损伤值明显减小，且损伤萌生位置越靠后，当管道壁厚为4.6 mm时，熔池下方内壁位置不会萌生损伤.
图13为不同管道壁厚下路径X4熔合线至内壁方向上各节点的损伤分布图，可以看出，壁厚方向上的损伤值随管道壁厚的增加而减小，且壁厚的增加有利于缩小熔合线附近损伤萌生区域. 这说明在役焊接管道壁厚越大，损伤萌生和烧穿失效的风险越小.
从温度T、累计塑性应变P和临界损伤断裂应变
$ {P}_{{\rm{cr}}} $ 的角度解释压力对在役焊接损伤失效的影响，图14展示了路径X4内壁节点温度、累计塑性应变和临界损伤断裂应变随管道壁厚的变化请况，可以看出，随着管道壁厚的增加，内壁节点的临界损伤断裂应变增大，而累计塑性应变减小，通过分析这种变化趋势可知管道壁厚越大，发生烧穿失效的风险越低；同时，内壁温度随管道壁厚的增大而逐渐降低，内壁温度是导致在役焊接烧穿失效的重要因素之一[7]，内壁温度的降低同样有利于降低烧穿失效的风险.![]()
图 14 路径X4温度、损伤值与临界损伤值对比Figure 14. Comparison of temperature, damage and critical value at path X45. 结论
(1) 基于Bonaro准则建立了X70管线钢高温损伤演化方程，通过在役焊接试验验证了该方程在预测在役焊接烧穿失效行为的准确性.
(2) 在役焊接过程中，熔池下方熔深最大处后方1 ~ 2 mm区域为失效高风险区，壁厚方向上，损伤值由熔合线向内壁逐渐减小，熔合线附近区域比内壁更容易萌生损伤，且该区域损伤值更大.
(3)临界损伤断裂应变随管道内压的增大而减小，随管道壁厚的增大而增加.
(4)降低管内介质压力、增大管道壁厚有利于降低在役焊接熔池下方萌生损伤甚至烧穿失效的风险.
-
![]()
图 2 不同送丝速度下焊道截面温度场分布及速度流线
Figure 2. Temperature distribution and velocity streamline of weld bead in different wire feed speeds. (a) 1.2 m/min; (b) 1.8 m/min; (c) 2.4 m/min; (d) 3.0 m/min; (e) 3.6 m/min; (f) 4.2 m/min
![]()
图 4 自由表面及熔池内部速度值
Figure 4. Velocity curve of free surface and internal molten pool. (a) Velocity curve of free surface on Path 1; (b) Velocity curve of internal molten pool on Path 2; (c) Velocity curve of free surface on Path 3; (d) Velocity curve of internal molten pool on Path4;
![]()
图 5 熔池表面温度梯度变化曲线
Figure 5. Temperature gradient curve of free surface. (a) Temperature gradient curve of free surface on horizontal direction; (b) Temperature gradient curve of free surface on vertical direction;
![]()
图 6 不同送丝速度下试验与模拟成形结果对比
Figure 6. Comparison of experiment and simulation result in different wire feed speeds. (a) 1.2 m/min; (b) 1.8 m/min; (c) 2.4 m/min; (d) 3.0 m/min; (e) 3.6 m/min; (f) 4.2 m/min
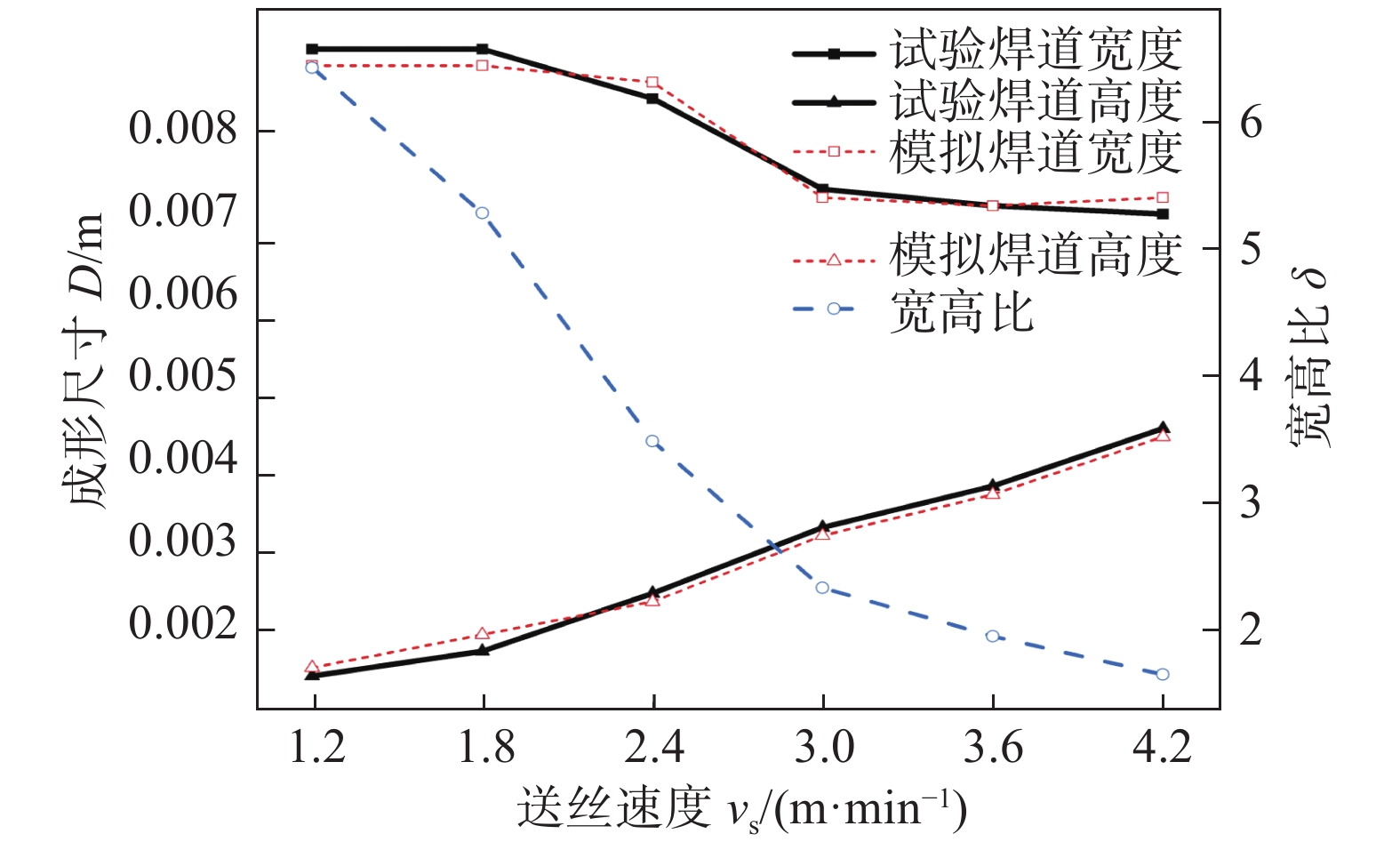
表 1 电弧增材试验结果
Table 1 Results of deposition experiment
送丝速度
vs/(m·min−1)宽度
w/m高度
h/m宽高比 焊道宏观形貌 1.2 0.009 0 0.001 4 6.42 
1.4 0.009 2 0.001 6 5.75 1.6 0.009 4 0.001 5 6.26 
1.8 0.009 0 0.001 7 5.29 2.0 0.008 4 0.002 0 4.20 
2.2 0.008 6 0.002 3 3.74 2.4 0.008 4 0.002 4 3.50 
2.6 0.008 4 0.002 5 3.36 2.8 0.007 7 0.002 8 2.75 
3.0 0.007 3 0.003 1 2.35 3.2 0.006 8 0.003 6 1.89 
3.4 0.007 1 0.003 4 2.09 3.6 0.006 6 0.003 6 1.83 
3.8 0.006 6 0.004 2 1.57 4.0 0.007 4 0.004 8 1.54 
4.2 0.007 0 0.004 3 1.63 
下载: 导出CSV
-
[1] 黄勇, 王新鑫, 瞿怀宇, 等. 工艺参数对耦合AA-TIG焊电弧阳极电流密度的影响[J]. 焊接学报, 2014, 35(2): 5 − 9. Huang Yong, Wang Xinxin, Qu huaiyu, et al. Effects of arc parameters on arc anode current density of coupling AA-TIG arc[J]. Transactions of the China Welding Institution, 2014, 35(2): 5 − 9.
[2] 张栋, 陈茂爱, 武传松, 等. 高速CMT焊送丝速度和焊接电流波形参数的优化[J]. 焊接学报, 2018, 39(1): 119 − 122. Zhang Dong, Chen Maoai, Wu Chuansong, et al. Optimization of waveform parameters for high speed CMT welding of steel[J]. Transactions of the China Welding Institution, 2018, 39(1): 119 − 122.
[3] Li A, Liu X, Yu B. Influence mechanism of processing parameters on size uniformity of 7075 aluminum alloy single tracks during liquid metal flow rapid cooling additive manufacturing[J]. Journal of Manufacturing Processes, 2020, 59: 258 − 265. doi: 10.1016/j.jmapro.2020.09.074
[4] Wang L, Chen J, Zhang S, et al. Numerical simulation of coupled arc-droplet-weld pool behaviors during compound magnetic field assisted gas metal arc welding[J]. AIP Advances, 2021, 11(6): 65221. doi: 10.1063/5.0049461
[5] 丁雪萍, 李桓. 焊接电流影响GMAW双丝焊电弧等离子体的数值模拟研究[J]. 机械工程学报, 2016, 52(16): 71 − 76. Ding Xueping, Li Huan. Numerical analysis for effect of welding current on arc plasma in double-wire GMAW[J]. Journal of Mechanical Engineering, 2016, 52(16): 71 − 76.
[6] 郭力玮, 黄继强, 冯音琦, 等. 环境压力对GMAW电弧能量耗散的影响[J]. 焊接学报, 2022, 43(2): 61 − 66. doi: 10.12073/j.hjxb.20210609003 Guo Liwei, Huang Jiqiang, Feng Yinqi, et al. Effect of ambient pressure on energy dissipation of GMAW arc[J]. Transactions of the China Welding Institution, 2022, 43(2): 61 − 66. doi: 10.12073/j.hjxb.20210609003
[7] Wang X, Fan D, Huang J, et al. A unified model of coupled arc plasma and weld pool for double electrodes TIG welding[J]. Journal of Physics D:Applied Physics, 2014, 47(27): 275002.
[8] Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201 − 225. doi: 10.1016/0021-9991(81)90145-5
[9] Ni M, Qin X, Hu Z, et al. Forming characteristics and control method of weld bead for GMAW on curved surface[J]. Advanced Manufacturing Technology, 2021, 119(3-4): 1883 − 1908.
[10] Bai X, Colegrove P, Ding J, et al. Numerical analysis of heat transfer and fluid flow in multilayer deposition of PAW-based wire and arc additive manufacturing[J]. International Journal of Heat and Mass Transfer, 2018, 124: 504 − 516. doi: 10.1016/j.ijheatmasstransfer.2018.03.085
[11] Hu Z, Hua L, Qin X, et al. Molten pool behaviors and forming appearance of robotic GMAW on complex surface with various welding positions[J]. Journal of Manufacturing Processes, 2021, 64: 1359 − 1376. doi: 10.1016/j.jmapro.2021.02.061
[12] 周祥曼, 王礴允, 袁有录, 等. 焊接速度对电弧增材熔池流动及焊道形貌影响的数值模拟研究[J]. 机械工程学报, 2022, 58(10): 103 − 111. Zhou Xiangman, Wang Boyun, Yuan Youlu, et al. Numerical Simulation Study of the Effects of Travel Speed on the Molten Pool Flow and Weld Bead Morphology of WAAM[J]. Journal of Mechanical Engineering, 2022, 58(10): 103 − 111.
[13] Tanaka M, Terasaki H, Ushio M, et al. A unified numerical modeling of stationary tungsten-inert-gas welding process[J]. Metallurgical and Materials Transactions. A, Physical Metallurgy and Materials Science, 2002, 33(7): 2043 − 2052. doi: 10.1007/s11661-002-0036-2
[14] 周祥曼, 刘练, 陈永清, 等. 外加变位磁场作用GTAW焊接电弧的数值模拟[J]. 三峡大学学报(自然科学版), 2021, 43(5): 101 − 106. doi: 10.13393/j.cnki.issn.1672-948x.2021.05.017 Zhou Xiangman, Liu Lian, Chen Yongqing, et al. Numerical simulation of GTAW welding arc under the external static magnetic field of changing position[J]. Journal of China Three Gorges University (Natural Sciences), 2021, 43(5): 101 − 106. doi: 10.13393/j.cnki.issn.1672-948x.2021.05.017
[15] Ji F, Qin X, Hu Z, et al. Influence of ultrasonic vibration on molten pool behavior and deposition layer forming morphology for wire and arc additive manufacturing[J]. International Communications in Heat and Mass Transfer, 2022, 130: 105789. doi: 10.1016/j.icheatmasstransfer.2021.105789
[16] Cho D W, Na S J, Cho M H, et al. A study on V-groove GMAW for various welding positions[J]. Journal of Materials Processing Technology, 2013, 213(9): 1640 − 1652. doi: 10.1016/j.jmatprotec.2013.02.015
-
期刊类型引用(1)
1. 周祥曼，王印权，王礴允，柏兴旺，付君健，田启华. 搭接中心距对电弧增材熔池流动及熔积层形貌影响的数值模拟. 材料热处理学报. 2024(03): 195-204 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 429
- HTML全文浏览量: 63
- PDF下载量: 97
- 被引次数: 1
