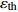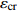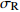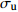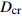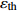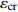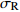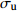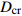Damage evolution model and numerical simulation of X70 pipeline steel of in-service welding
-
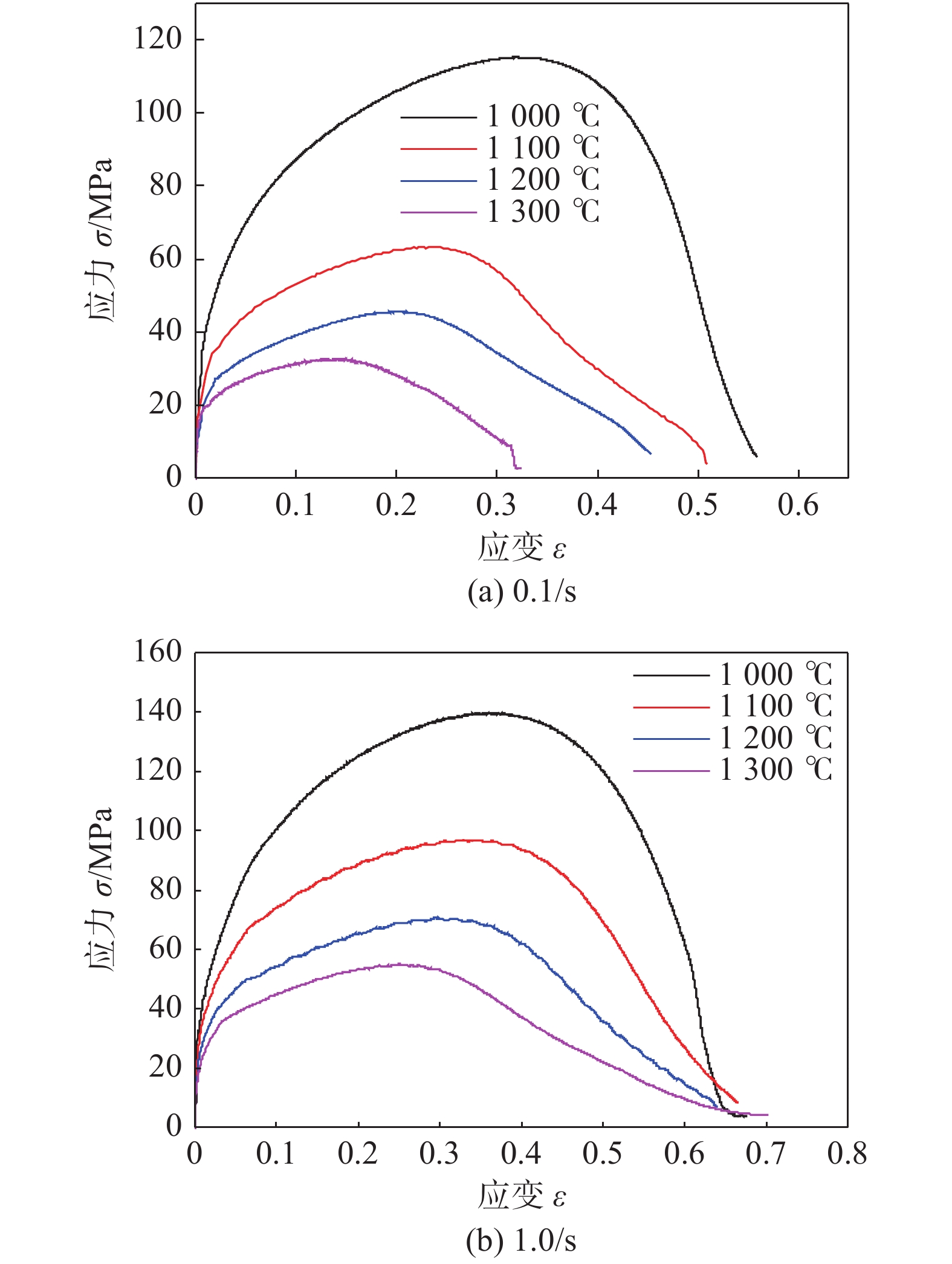
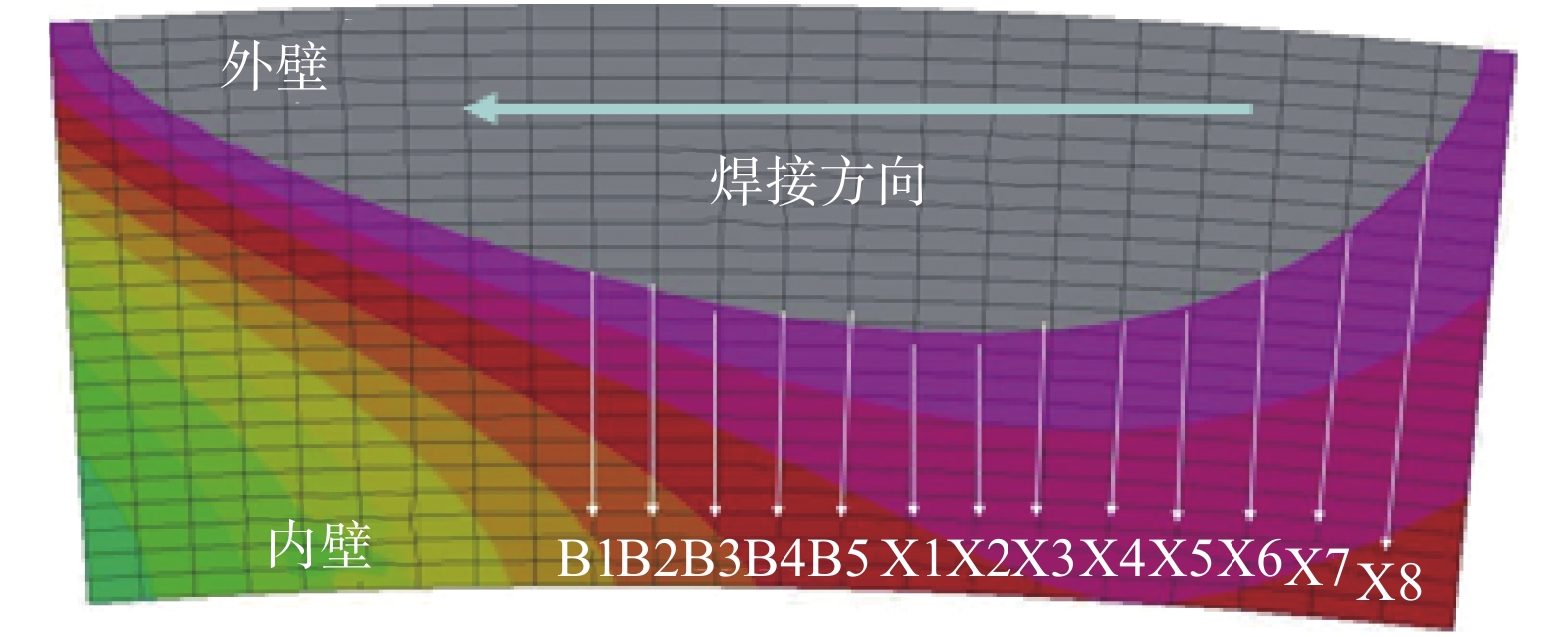
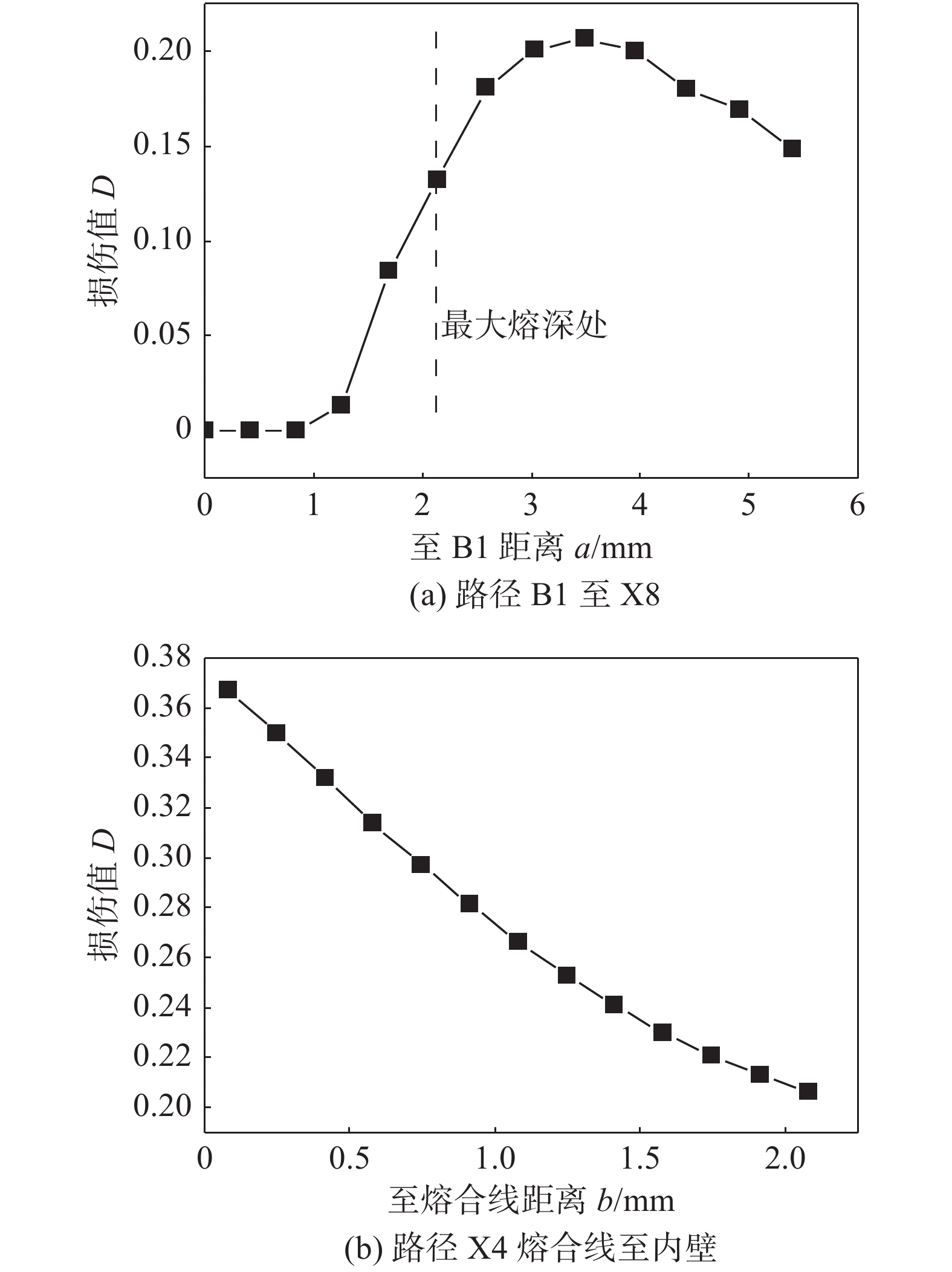
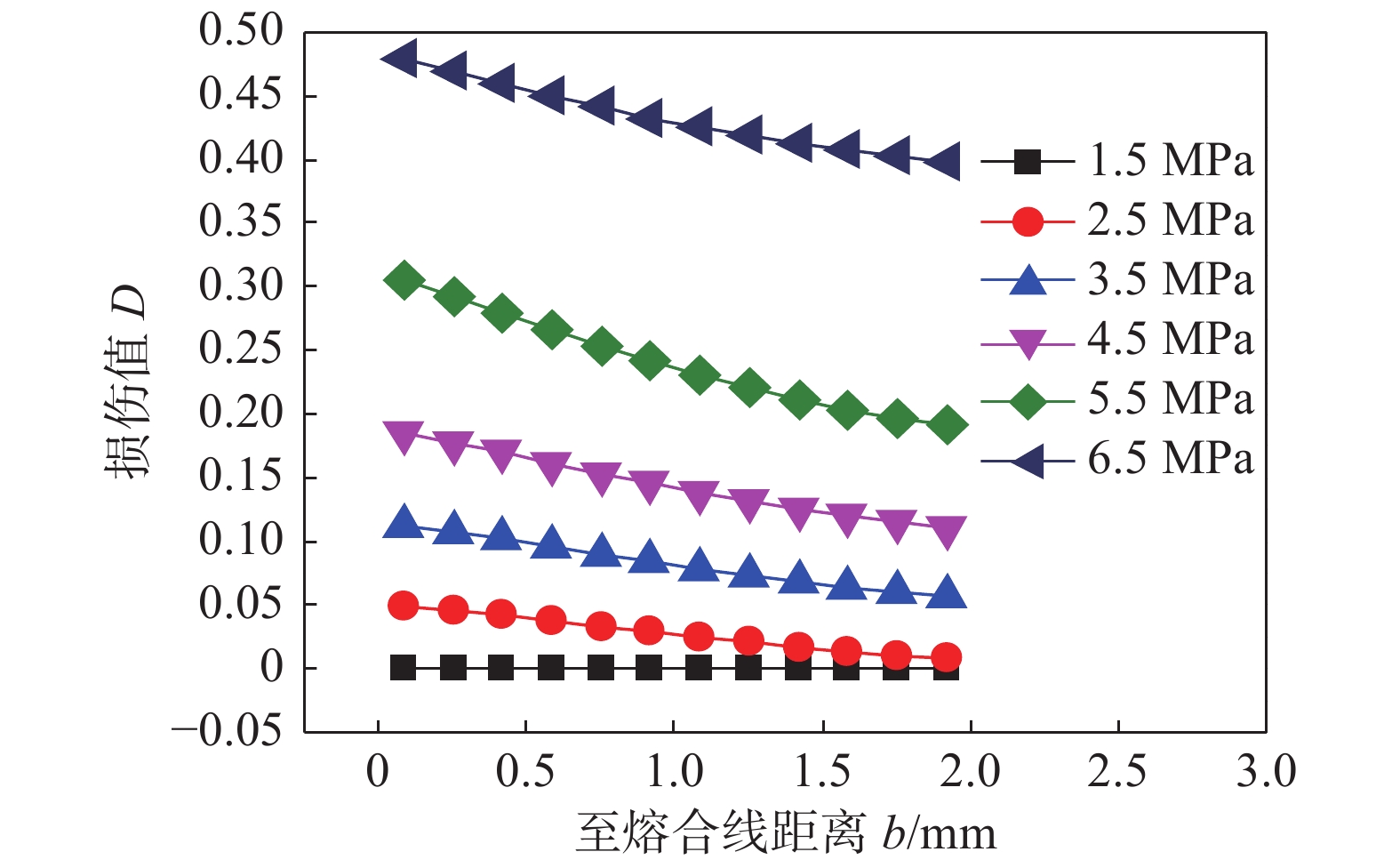
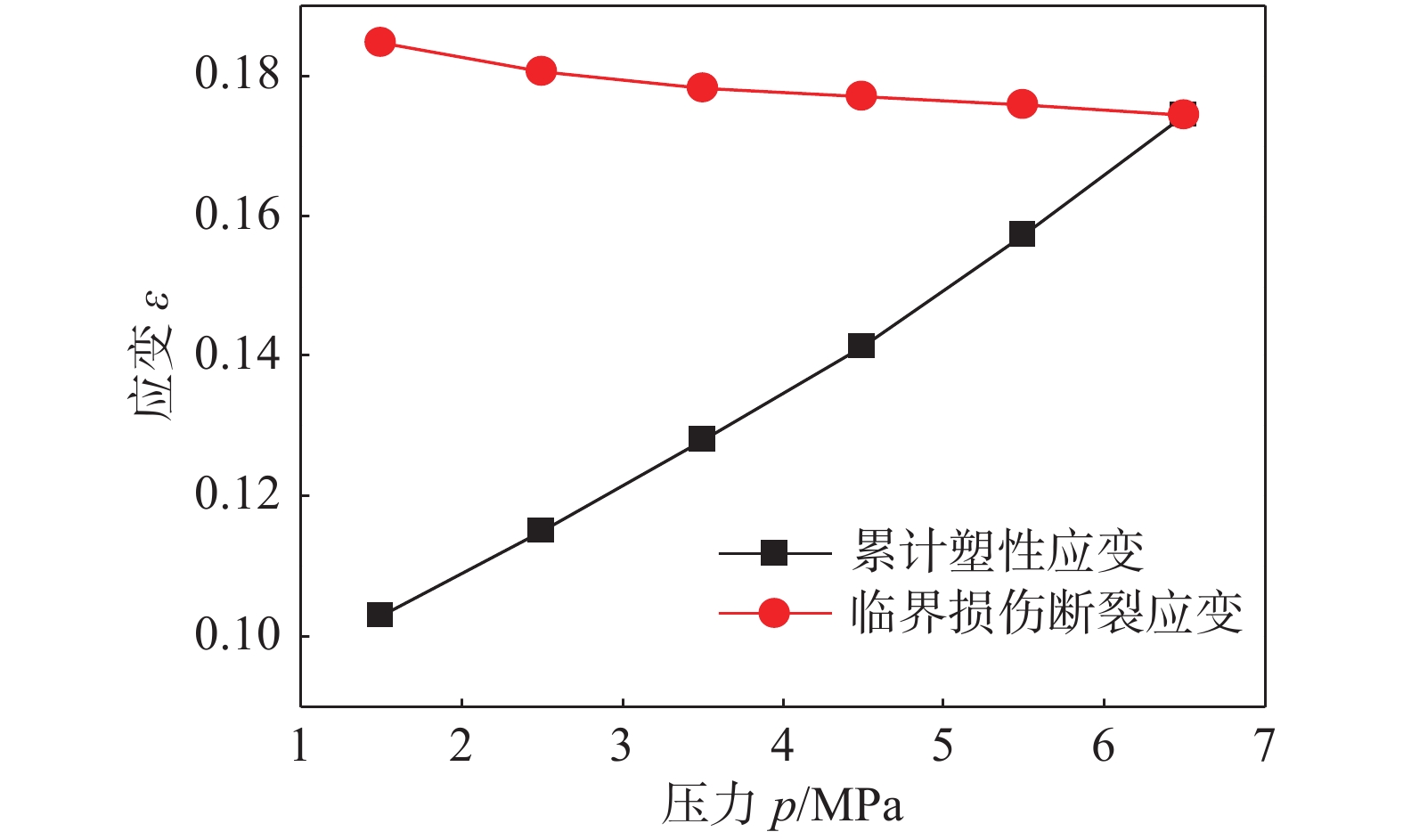
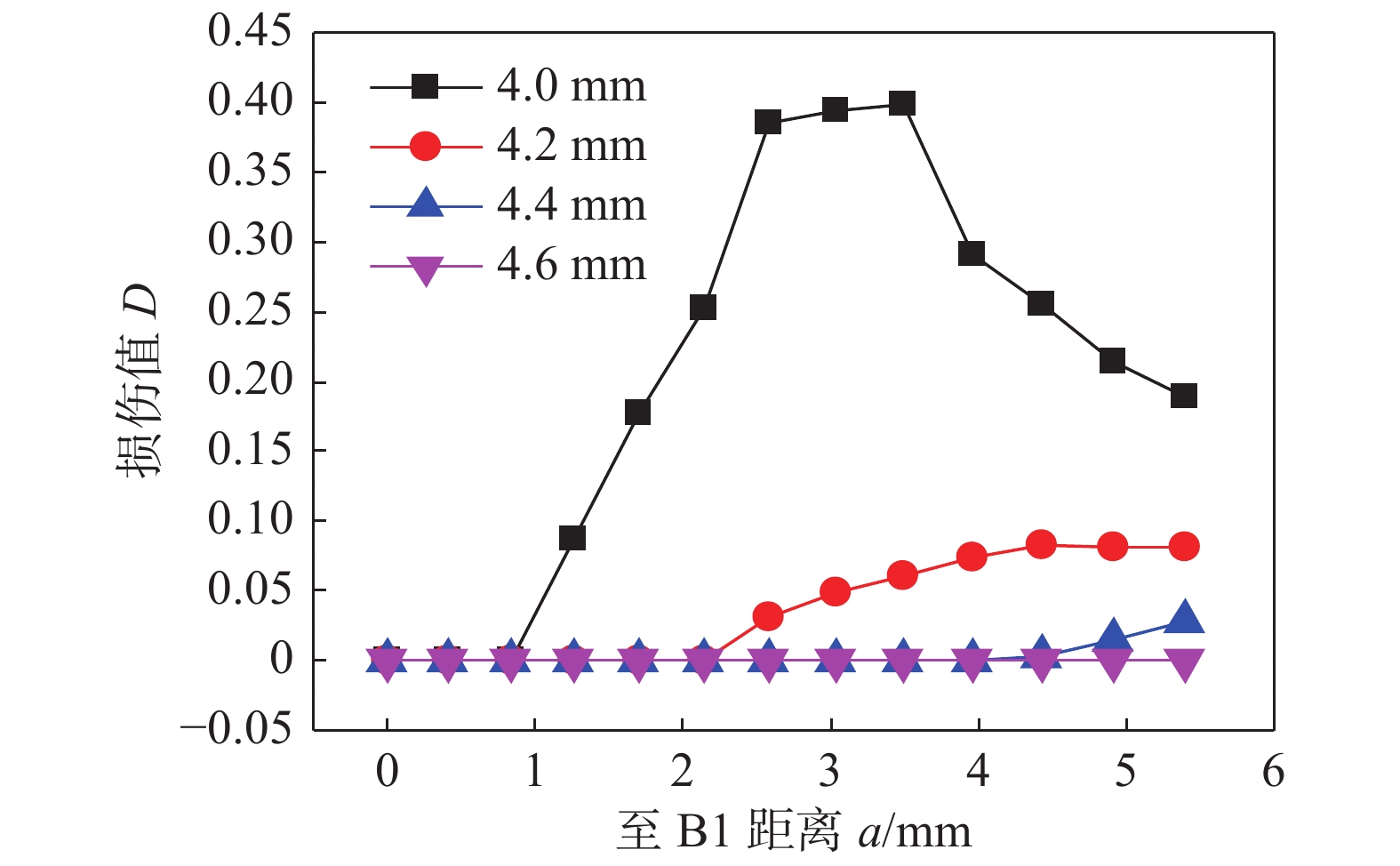
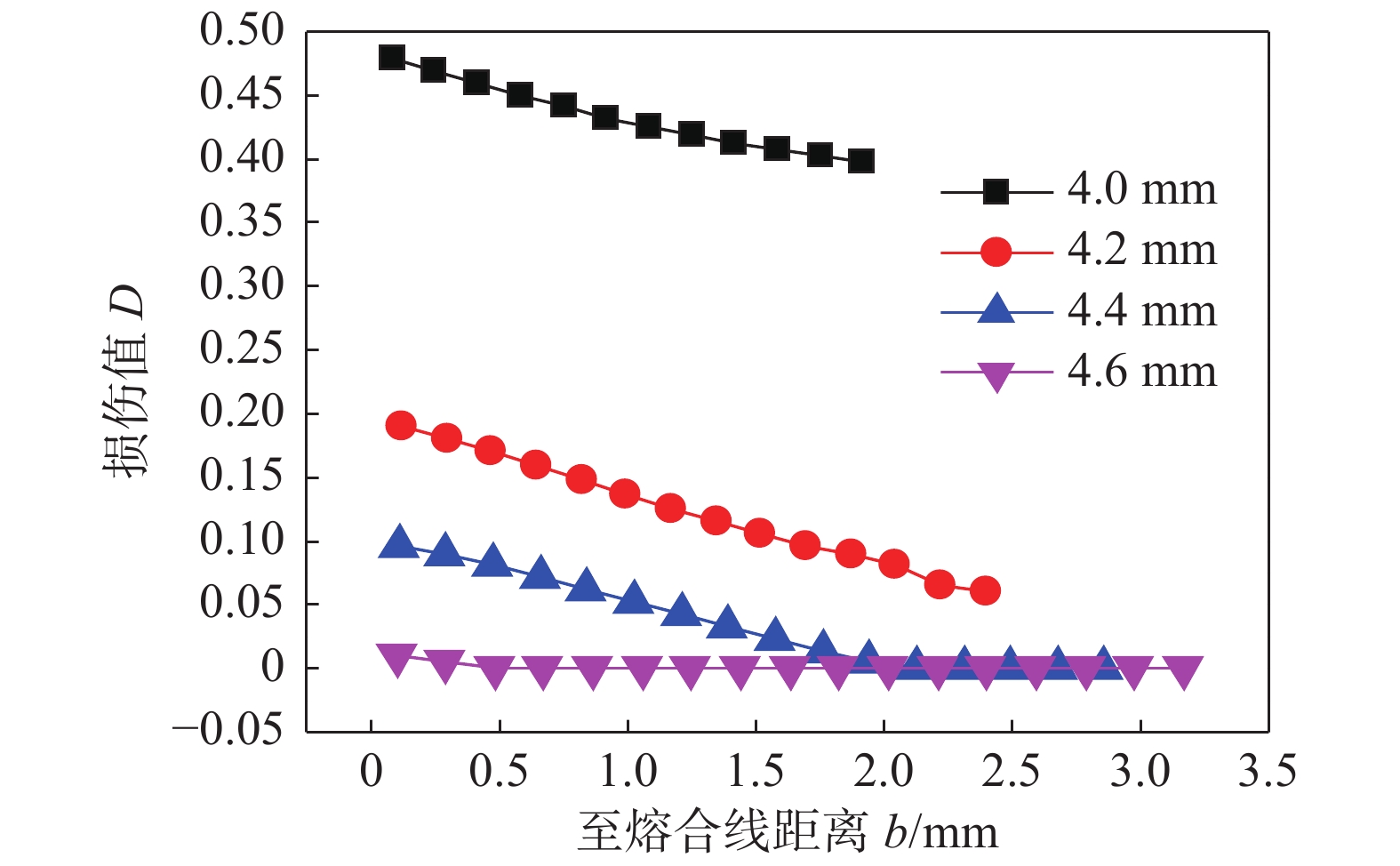
摘要: 以X70管线钢为研究对象，进行了不同温度和应变速率下的高温拉伸试验，获得了初始损伤阈值应变、临界损伤断裂应变、临界损伤值等损伤模型参数，建立了基于BONARO模型的损伤演化方程；模拟在役焊接损伤演化过程，并与在役焊接试验结果对比，研究介质压力、壁厚对在役焊接损伤演化行为的影响规律，研究发现在役焊接过程中，熔池下方内壁处最大熔深处后方1 ~ 2 mm区域为失效高风险区，损伤值在壁厚方向上由熔合线向内壁递减，管内介质压力的减小、壁厚的增大都会在一定程度上减小在役焊接过程中熔池下方的损伤值，从而减小烧穿失效的风险.Abstract: In this paper, X70 pipeline steel was taken as the research object. High temperature tensile tests were carried out at different temperatures and strain rates. Damage model parameters such as the threshold strain, critical damage strain and critical damage were obtained, and damage evolution equations based on BONARO model was established. The damage evolution process of in-service welding was simulated and compared with the experimental results of in-service welding. The influence rules of medium pressure and wall thickness on the damage evolution behavior of in-service welding were studied. It was found that: during the in-service welding process, molten pool below the maximum damage value of the inner wall is located in the largest fusion deep behind the 1mm to 2 mm area, damage value in thickness direction decreases from the fusion line to the inner wall; decreasing inner medium pressure and increasing the wall thickness can reduce the damage at the bottom of molten pool, thus reduce the risk of burn through.
-
Keywords:
- in-service welding /
- burn through /
- damage
-
0. 序言
残余应力和变形是焊接过程中常见的问题，会对焊接工件的质量和性能产生重要影响，因此，预测焊接残余应力和变形已经成为焊接领域中的重要研究内容. 焊接工艺参数，焊后残余应力及变形之间是一种非常复杂的非线性映射关系，在厚板焊接中对焊接残余应力与变形影响较大的填充层焊接工艺参数主要有焊接电流、电弧电压、焊接速度以及层间温度[1-3]. 焊接残余应力与变形的预测是高度非线性问题，很难用简单的数学模型来描述，需要通过各种方法和经验对其中的权重和因子进行计算.
人工神经网络可实现复杂非线性系统的建模和预测，具有强大的联想能力、容错能力以及自适应学习能力，近年来在焊接质量预测中得到了广泛关注[4-7]，其中BP神经网络是人工神经网络一种常用的深度学习模型，可以在没有大量数据的情况下进行预测，BP神经网络具有较强的自适应学习能力和非线性拟合能力，已有诸多学者将其应用于非线性领域的预测中，例如Shanavas等人[8] 通过建立反向传播神经网络模型，来预测铝合金搅拌摩擦焊焊缝的抗拉强度和伸长率，模型预测误差小于5%；马思群等人[9] 采用BP神经网络的方法对铝合金车体的焊接残余应力进行预测，预测误差在8%以内.
传统的BP神经网络在训练过程中容易出现梯度消失或梯度爆炸等问题，导致模型训练困难或预测效果不佳，遗传算法是一种优化算法，可用于解决复杂问题时寻找最优解，近年来遗传算法在神经网络优化方面得到了广泛应用，研究表明遗传算法可以在一定程度上解决BP神经网络训练困难的问题，从而提高模型的预测精度[10-11]，例如张天鹏等人[12] 基于GA-BP神经网络来预测FSW接头的性能，结果表明，实际值与预测值之间的误差在5%左右，具有较高的预测精度；关子奇等人[13] 采用GA遗传算法来优化BP神经网络模型来预测焊接熔池照度，试验结果表明，优化后的GA-BP神经网络模型对焊接熔池照度的预测更为精准；张永波等人[14] 基于GA-BP神经网络对带钢焊接质量进行预测，结果表明，与传统的BP神经网络模型相比，通过遗传算法对BP神经网络的权值和阈值进行优化，改良后的模型无论是在精度上还是在收敛速度上都有了大幅度的提升.
文中探讨基于遗传算法优化的BP神经网络在316L中厚板TIG焊的焊接残余应力和变形预测中的应用. 首先，采用正交试验的方法获取焊接工艺参数，残余应力和变形之间的典型样本数据；然后，介绍传统BP神经网络的原理和在焊接残余应力及变形预测中的应用；其次，介绍遗传算法的基本原理和应用优势，并探讨其在BP神经网络优化中的作用；最后，结合具体的焊接试验对两种神经网络模型的预测结果分别进行验证和误差计算，并对基于遗传算法优化的BP神经网络，在焊接残余应力和变形预测中的预测精度以及该方法的收敛速度等优缺点进行讨论.
1. 试验设计
1.1 试验方法
试验使用的焊机为松下YC-500WX5，焊丝牌号为TGS-316L，保护气体为全氩气，焊接试板材料为316L不锈钢，尺寸为300 mm × 300 mm × 20 mm，采用U形7.5°坡口，钝边为1.5 mm，装配间隙为2.5 mm，施焊20层，每层为多道焊，每层焊厚不超过2 mm. 打底层采用的焊接电流为60 A，电弧电压为12 V，焊接速度为50 mm/min，盖面层采用的焊接电流为180 A，电弧电压为17 V，焊接速度为80 mm/min.
为了测量不同填充层焊接工艺参数对焊接变形的影响，在考虑焊接工装夹的情况下，最终采用反变形的方法来测量计算每块试验样板最终的角变形，如图1所示，并通过点焊的方式将每块试板的反变形角度统一固定为20°，此外，为了焊接时能够避免起弧和落弧留在试板上，造成对接板件边缘焊接缺陷，保证所有试板宽度范围内的焊缝都能够达到相同的强度，在每对焊接试板的焊缝两端各放置一块引弧板，通过点焊连接，见图1(b).
![]()
图 1 焊接试板反变形示意图Figure 1. Welding indication. (a) Sketch of striking arc, ending arc and spot welding position; (b) Sketch of the anti-deformation of the welding test plate对焊缝填充层焊接工艺参数，采用正交试验设计L16(44)因素水平表，并以填充层采用的焊接电流、电弧电压、焊接速度及层间温度为因素，经过综合分析试验材料的板厚、材质以及焊接顺序等确定焊接工艺参数的水平值，具体参数见表1.
表 1 因素水平表L16(44)Table 1. Factor level table for L16(44)水平
编号焊接电流
I/A电弧电压
U/V焊接速度
v/(mm·min−1)层间温度
T/℃1 A1(140) B1(14) C1(50) D1(80) 2 A2(165) B2(16) C2(90) D2(120) 3 A3(190) B3(18) C3(120) D3(160) 4 A4(215) B4(20) C4(150) D4(200) 1.2 残余应力及变形测量
试板上的残余应力并不是处处相同，测量时采用焊缝方向和垂直于焊缝方向上均匀取点的方法进行测量，图2为沿焊缝横向和纵向的残余应力测试点分布示意图，其中测试点有13个，沿垂直焊缝方向的残余应力测试点分别在距焊缝中心20，50，80，110，140 mm处；而沿着焊缝方向的测试点，即A，B，C，D，E，F，G，H，I，每个点之间间距为30 mm. 由于盲孔法测残余应力的局限性，文中所测残余应力均为试板近表面残余应力，将测试结果进行比较，得出焊缝近表面横纵向最大残余应力.
![]()
图 2 试板的残余应力测试取点示意图(mm)Figure 2. Sketch of the point selection for residual stress testing of the test plate如图3所示，试验采用盲孔法测量316L试板焊缝近表面的残余应力，使用角度尺等工具测量试板焊接角变形，并将测得的数据作为样本数据集应用于焊接残余应力和变形预测模型的训练.
![]()
图 3 盲孔法测量残余应力示意图Figure 3. Schematic diagram of the blind hole method for measuring residual stress1.3 正交试验
按照L16(44)正交试验的方法测得的试验结果见表2，在打底层和盖面层的焊接参数相同的条件下，填充层不同的焊接工艺参数对焊接残余应力和角变形的影响程度是显著不同. 横向最大残余应力第6组最大，为444.5 MPa；第18组最低，为123.9 MPa，相差320.6 MPa；纵向最大残余应力第10组最大，为494.3 MPa；第17组最小，为136.7 MPa，相差357.6 MPa；角变形第14组最大，为9.84°；第一组最小，为6.18°，相差3.66°.
表 2 正交试验结果Table 2. Results of the orthogonal experiment序号 焊接电流
I/A电弧电压
U/V焊接速度
v/(mm·min−1)层间温度
T/℃横向最大残余应力
σx-max/MPa纵向最大残余应力
σy-max/MPa角变形
θ/(°)1 140 14 50 80 124.4 386.7 6.18 2 140 16 90 120 287.6 275.8 7.56 3 140 18 120 160 237.3 241.9 6.93 4 140 20 150 200 413.3 187.6 7.42 5 165 14 90 200 397.6 284.3 7.12 6 165 16 50 160 444.5 365.8 7.88 7 165 18 120 120 315.3 397.2 9.33 8 165 20 150 80 274.3 426.3 8.52 9 190 14 120 120 356.1 468.4 8.78 10 190 16 150 80 333.1 494.3 8.81 11 190 18 50 200 297.6 412.6 9.24 12 190 20 90 160 183.7 471.8 8.38 13 215 14 150 160 244.2 356.1 9.56 14 215 16 120 200 174.3 337.1 9.84 15 215 18 90 120 211.3 387.5 9.36 16 215 20 50 80 193.5 434.8 9.21 17 163 17 120 88 163.1 136.7 8.41 18 175 18 110 165 123.9 256.8 8.65 19 185 15 100 95 263.4 313.7 8.93 20 210 19 135 145 309.8 351.8 9.43 2. 神经网络预测
2.1 BP神经网络
BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络模型之一[15]，具有任意复杂的模式分类能力和优良的多维函数映射能力. 在网络结构上，BP神经网络由输入层、隐含层、输出层组成；在计算方法上，BP神经网络以网络误差平方为目标函数，利用梯度下降法来计算目标函数的最小值，因此，BP神经网络在解决非线性拟合的问题上具有巨大的优势[16] .
BP神经网络的主要特点是信号前向传播，误差反向反馈传播，设定期望输出，网络根据预测输出与期望输出的误差对比结果进行反向传播，调整各神经元的权值和阈值，整个过程反复进行，直到网络样本输出误差小于期望误差精度或训练达到最大迭代次数为止[17] .
图4为神经网络结构示意图，x1，x2，x3，x4是神经网络模型的输入, y1，y2，y3是网络的输出，整个神经网络模型可以看成一个非线性函数，网络的输入x1，x2，x3，x4是自变量，网络的输出y1，y2，y3为因变量，自变量和因变量构成了函数映射关系. 假设
$ f $ 为激活函数的映射关系，将该神经网络的隐藏层神经元激活函数设定为Sigmoid函数, 将输出层神经元激活函数设定为Purelin线性函数.Sigmoid函数公式为
$$ f\left(x\right)=\frac{1}{1 + {e}^{-x}} $$ (1) Purelin线性函数公式为
$$ f\left(x\right)=x $$ (2) 故此时前向传播公式为
$$ {u}_{j}=f\left({\sum }_{i=1}^{n}{v}_{ij}{x }_{i} + {\theta }_{j}^{u}\right)，j={\mathrm{1,2},\cdots ,}m $$ (3) $$ y=f\left({\sum }_{j=1}^{m}{w}_{j}{u}_{j} + {\theta }^{y}\right) $$ (4) 为了推演方便，先拿第k个对象作为目标，假设
$ {y}^{\left(k\right)} $ 为经过神经网络预测出的值，$ {y}^{{\left(k\right)}^{'}} $ 为真实的输出值, 为了得到真实值与预测值之间误差尽可能小的目标，将目标函数设定为$$ J=\sum _{k}^{\infty }{\left({y}^{\left(k\right)}-{y}^{{\left(k\right)}^{'}}\right)}^{2} $$ (5) 式中假设
$ {v}_{ij} $ 为第i个输入变量与第j个隐藏神经元的权重，$ {\mathrm{\theta }}_{j}^{u} $ 为隐藏层u第j个神经元的阈值，或者称为偏置项，$ {w}_{j} $ 为第j个神经元与y连接的权重，$ {\mathrm{\theta }}^{y} $ 为y的偏置，$ {u}_{j} $ 为隐藏层第j个神经元，$ {v}_{ij} $ ，$ {\theta }_{j}^{u} $ ，$ {w}_{j} $ ，$ {\theta }^{y} $ 为需要确定的网络参数. 可以采用梯度下降法对网络参数和目标函数$ J $ 进行权重更新和优化，其中$ \mu $ 为学习率.$$ {\nu }_{ij}^{'}={v}_{ij}-\mu \frac{dJ}{d{v}_{ij}} $$ (6) $$ {w}_{j}^{'}={w}_{j}-\mu \frac{dJ}{d{w}_{j}} $$ (7) $$ {\theta }_{j}^{u'}={\theta }_{j}^{u}-\mu \frac{dJ}{d{\theta }_{j}^{u}} $$ (8) $$ {\theta }^{y'}={\theta }^{y}-\mu \frac{dJ}{d{\theta }^{y}} $$ (9) 式中：
$ {v}_{ij}\mathrm{'} $ ，$ {\theta }_{j}^{u'} $ ，$ {{w}_{j}}' $ ，$ {\theta }^{y'} $ 为更新以后的网络参数，通过不断迭代更新网络参数，当样本训练输出误差小于期望误差或者达到最大迭代次数时，得到的网络参数就是训练之后的最佳神经网络模型.目标函数对各神经网络中参数的微分由反向梯度下降公式求得
$$ \frac{\partial {J}^{\left(k\right)}}{\partial {w}_{j}}=2\left({y}^{\left(k\right)}-{y}^{\left(k\right)'}\right){u}_{j} $$ (10) $$ \frac{\partial {J}^{\left(k\right)}}{\partial {\theta }^{y}}=2\left({y}^{\left(k\right)}-{y}^{\left(k\right)'}\right) $$ (11) $$ \frac{\partial {J}^{\left(k\right)}}{\partial {\nu }_{ij}}=2\left({y}^{\left(k\right)}-{y}^{\left(k\right)'}\right){w}_{j}{u}_{j}\left(1-{u}_{\dot{j}}\right){x}_{i}^{\left(k\right)} $$ (12) $$ \frac{\partial {J}^{\left(k\right)}}{\partial {\theta }_{j}^{u}}=2\left({y}^{\left(k\right)}-{y}^{\left(k\right)'}\right){w}_{j}{u}_{j}\left(1-{u}_{\dot{j}}\right) $$ (13) 在BP神经网络训练学习过程中，网络的初始权值对学习效果和收敛速度有着至关重要的影响，合适的初始值可以使网络模型较快收敛到最优解，如果初始权值和阈值选取不当，会导致网络的收敛速度慢并且容易陷入局部最小值，由于BP神经网络的初始权值是随机赋予的，因此非常容易出现收敛速度慢且易陷入局部最小值的问题[18] .
采用遗传算法来优化BP神经网络的初始权值和阈值，以提高网络输出的准确性和速度，从而加速BP神经网络的收敛速度，解决局部极值问题，再通过BP神经网络的反向传播算法来寻找整个网络参数的最优解，以实现更好的预测效果.
2.2 GA-BP神经网络
遗传算法是一种模拟自然界遗传机制，以达尔文的生物进化论为理论基础，通过数学利用仿真运算的过程搜索最优解算法. 利用遗传算法，首先需要创建初始种群，选择种群规模为
$ M $ ，取网络所有权值和阈值组成$ N $ 维向量，随机生成一个$ M\cdot N $ 的矩阵作为初始种群，其中N=inputnumber·hiddennumber + hiddennumber + hiddennumber·outputnumber + outputnumber，适应度是遗传算法中衡量个体性能的主要指标，根据适应度的大小对个体进行筛选，因此，适应度是遗传算法的动力. 由于遗传算法的复杂度主要取决于适应度函数的复杂度，因此适应度函数的设计应尽可能简单，以减少算法的计算时间.遗传算法首先需要对初始值进行编码，由于BP神经网络采用了Sigmoid函数作为激活函数，其权值和阈值介于−1 ~ 1，因此采用实数编码会比二进制编码更合适. 误差与适应度为相反的关系，当适应度越好时，预测的结果越准确，误差值越小，因此采用均方误差的倒数作为适应度函数.
适应度函数的公式为
$$ F\left(x\right)=\frac{1}{J\left(x\right)} $$ (14) 遗传算法主要包括选择操作、交叉操作和变异操作，在进行选择操作时，个体被选中的概率与适应度相关，当个体的适应度越大，被选中的可能性就越大，因此最常用到的方法就是轮盘赌法，每个个体被选择的概率为
$$ {p}_{i}=\frac{{F}_{i}}{\displaystyle\sum _{i=1}^{N}{F}_{i}} $$ (15) 式中：
$ {F}_{i} $ 为个体$ i $ 的适应度函数值；$ N $ 为种群个体数量.在进行交叉操作时，将第
$ k $ 条染色体$ {a}_{k} $ 和第$ l $ 条染色体$ {a}_{l} $ 同时在$ j $ 位置进行交换，交换方式如下$$ {a}_{kj}={a}_{kj}\left(1-b\right) + {a}_{lj}b $$ (16) $$ {a}_{lj}={a}_{lj}\left(1-b\right) + {a}_{kj}b $$ (17) 式中：b是[0,1]的随机数.
在进行变异操作时，通过选择第
$ i $ 个个体的第$ j $ 个基因$ {a}_{ij} $ 进行变异，具体操作方法如下$$ {a}_{ij}=\left\{\begin{array}{c}{a}_{ij} + {(a}_{ij}-{a}_{\max})\cdot f(g),r > 0.5\\ {a}_{ij} + {(a}_{\min}-{a}_{ij})\cdot f(g),r\leqslant 0.5\end{array}\right. $$ (18) $$ f\left(g\right)=r{\cdot \left(1-\frac{g}{{G}_{\max}}\right)}^{2} $$ (19) 式中：
$ {a}_{\max} $ 与$ {a}_{\min} $ 分别是基因$ {a}_{ij} $ 的上限和下限；$ r $ 是0 ~ 1之间的随机数；$ g $ 是当前迭代次数；$ {G}_{\max} $ 是最大进化次数.在传统的BP神经网络之前，使用遗传算法进行编码、选择、交叉和变异操作，以优化网络的初始权值和阈值，这种改进避免了传统生物神经网络随机初始化带来的问题，例如网络陷入局部最小值. 遗传算法可以确定最佳的初始权值和阈值，从而解决了传统BP神经网络的局限性，图5为GA-BP神经网络的算法流程图.
3. 仿真试验验证
3.1 数据预处理
经过正交试验L16(44)共获得16组残余应力和角变形的实测数据，再分别采用不同的焊接工艺参数随机进行4组试验，一共获得20组试验数据. 试验取前16组数据作为训练样本，用于GA-BP神经网络的学习和训练，取后4组随机的试验数据作为验证样本，用于验证神经网络的预测精度和泛化能力.
考虑到输入层各个参数之间差异比较大，故对输入层的样本数据采用Mapminmax函数进行归一化处理，将数值变换到0 ~ 1，目的在于消除因量纲不同对预测结果造成的影响，具体消除方法如下
$$ {x}^{*}=\frac{\left(x-{x}_{\min}\right)({y}_{\max}-{y}_{\min})}{{x}_{\max}-{x}_{\min}} + {y}_{\min} $$ (20) 式中：
$ {y}_{\max} $ 和$ {y}_{\min} $ 为设定的上下限，分别为1和0；$ x $ 是待归一化的样本数据；$ {x}_{\max} $ 和$ {x}_{\min} $ 分别为样本数据的最大值和最小值；$ {x}^{*} $ 是样本数据归一化处理后得到的结果.3.2 仿真试验
为了验证改进后的遗传算法对焊接残余应力和变形有良好的预测效果，因此需要进行仿真试验，数据集为上述预处理后的数据，在Matlab2021b中对预测模型进行训练，结果表明，利用遗传算法优化后的BP神经网络模型，对焊接残余应力和变形的预测在预测精度和泛化能力方面比传统的BP神经网络效果要好.
文中的仿真试验，通过焊接电流、电弧电压、焊接速度以及层间温度来预测焊接之后的残余应力和变形，因此输入层节点为4个，输出层节点为3个，关于隐含层的节点数根据经验公式手动设定
$$ m_1=\sqrt{a + b} + k $$ (21) 式中：
$ m_1 $ 为隐含层节点数；$ a $ 和$ b $ 分别为输入层和输出层的节点数；$ k $ 为1 ~ 10之间的常数.3.3 参数设定
采用神经网络对模型训练时，隐藏层设定为两层，在Matlab中的基本参数设置如下.
(1) net.trainParam.epochs=100，迭代次数为100次.
(2) net.trainParam.lr=0.1，学习率为0.1.
(3) net.trainParam.goal=0.001，训练目标误差为0.001.
设置遗传算法的迭代次数为50，种群规模为20，发生交叉的初始概率为0.6，变异概率为0.4.
3.4 仿真结果及分析
使用Matlab2021b软件分别对BP神经网络和GA-BP神经网络进行训练，预测结果与实际值比较结果如图6所示.
![]()
图 6 BP和GA-BP神经网络训练和预测结果Figure 6. Training and prediction results of BP and GA-BP neural networks. (a) maximum lateral residual stress of the training sample； (b) maximum longitudinal residual stress of training sample； (c) training sample deformation angle； (d) test the maximum lateral residual stress of the sample； (e) longitudinal maximum residual stress of the sample is tested； (f) test sample deformation angle通过对比优化前后神经网络模型的预测输出以及期望输出分析神经网络的预测效果，从图6中可以看出，BP神经网络模型的预测较不稳定，在个别样本点的预测误差较大，在少数样本点以及测试点的预测精度较高，因此BP神经网络模型的数据拟合能力和预测性都不够稳定. 对比图6中这6张图不难看出，无论是训练样本还是测试样本，GA-BP神经网络的预测值比BP神经网络更接近于实际测量值，拟合程度更高，预测效果更好.
BP和GA-BP神经网络适应度曲线如图7所示，GA-BP神经网络的收敛速度和训练效率都明显高于BP神经网络，通过对比两种模型的适应度曲线，可以看出BP网络的曲线波动更大，GA-BP网络的曲线更加平滑，这表明优化后的网络模型收敛更快，训练更加稳定，优化后网络的最佳适应度值更低，模型的预测结果与实际结果之间的差异更小，预测结果更好.
![]()
图 7 适应度变化曲线Figure 7. Curves of fitness changes. (a) BP neural network; (b) GA-BP neural network神经网络预测平均相对误差见表3，BP神经网络对横、纵向残余应力和角变形的训练样本预测误差分别为12.15%，12.52%，6.8%，GA-BP神经网络的训练样本预测误差分别为2.51%，2.01%，1.28%，由此可见优化后的网络模型预测效果显著提高. BP神经网络的测试集的预测误差分别为14.56%，14.35%，8.53%，GA-BP神经网络的预测误差分别为2.38%，2.84%，1.32%，优化后的网络模型无论是在训练集还是测试集上的表现都优于传统的BP神经网络. GA-BP神经网络预测模型在预测结果上有了一定的改善，在预测精度上明显优于传统的BP神经网络模型，平均相对误差在3%以内.
表 3 神经网络预测平均相对误差Table 3. Average relative error of neural network prediction输出结果 BP GA-BP 训练样本 测试样本 训练样本 测试样本 横向最大残余应力 12.15% 14.56% 2.51% 2.38% 纵向最大残余应力 12.52% 14.35% 2.01% 2.84% 角变形 6.8% 8.53% 1.28% 1.32% 试验结果表明，根据正交试验和预测值不难发现相对于电弧电压，焊接电流对残余应力和角变形的影响更大，随着电流电压的增大，残余应力呈现上升趋势，同时变形也在增大.
通过对比表中的平均相对误差表值，可以得出GA-BP模型比BP网络模型的误差小，预测的精度更高，通过采用随机试验的方式验证模型的预测精度和误差，可以发现模型的泛化能力很好，并且优化后模型的泛化能力比传统BP神经网络模型表现更加优异，通过对比两组模型的训练迭代次数和适应度曲线图，可以发现GA-BP的收敛速度要明显好于BP，因此GA-BP的收敛性更好，总体效果更好.
4. 结论
(1) BP神经网络的预测相对误差在15%以内，而GA-BP神经网络的预测相对误差能控制在3%以内，因此GA-BP神经网络比传统的BP神经网络预测效果更好，拟合能力更突出，并且模型的收敛速度更快，训练过程更稳定.
(2) GA-BP神经网络模型对横、纵向残余应力以及角变形的真实值随机测试预测误差分别为2.38%，2.84%，1.32%，结果表明，GA-BP神经网络能够精准得反映多层多道焊填充层焊接工艺参数与焊后残余应力之间的非线性映射关系，相对误差小，具有较强的预测能力和泛化能力，该方法对奥氏体不锈钢中厚板多层多道焊填充层焊接工艺参数具有指导作用，并对焊后残余应力和变形控制提供了一种新的思路和方法，在焊接过程中发挥了重要作用.
-
![]()
图 3 管道模型
Figure 3. Model of the pipeline. (a) 3D model of half pipeline; (b) 2D model of welded joint
![]()
图 5 不同路径损伤分布
Figure 5. Distribution of damage values in differnet paths. (a) Path from B1 to X8; (b) Path X4 from weld line to the inner wall
![]()
图 8 损伤值与临界损伤值的对比
Figure 8. Comparison of damage and critical value. (a) 5.5 s; (b) 5.75 s
![]()
图 9 不同压力下的损伤分布(B1-X8)
Figure 9. Distribution of damage values at different pressure (B1-X8)
![]()
图 14 路径X4温度、损伤值与临界损伤值对比
Figure 14. Comparison of temperature, damage and critical value at path X4
表 1 在役焊接试验相关工艺参数
Table 1 Welding parameters of in-service welding
序号 焊接电流 I/A 焊接电压 U/V 焊接速度 v/(mm·s−1) 热输入 Q/(J·mm−1) 压力 P/MPa 烧穿情况 1 255 13.7 4 870 6.5 未烧穿 2 260 13.8 4 890 6.5 未烧穿 3 265 13.7 4 910 6.5 未烧穿 4 270 13.8 4 930 6.5 未烧穿 5 275 13.9 4 955 6.5 未烧穿 6 280 14.0 4 980 6.5 烧穿 
下载: 导出CSV
表 2 损伤模型参数结果
Table 2 Damage model parameter results
温度T/K 应变速率0.1/s 应变速率1.0/s 初始损伤阈值应变 $ {\varepsilon }_{{\rm{th}}} $ 临界断裂应变 $ {\varepsilon }_{{\rm{cr}}} $ 断裂应力 $ {\sigma }_{{\rm{R}}} $ /MPa峰值应力 $ {\sigma }_{{\rm{u}}} $ /MPa临界损伤值 $ {D}_{{\rm{cr}}} $ 初始损伤阈值应变 $ {\varepsilon }_{{\rm{th}}} $ 临界断裂应变 $ {\varepsilon }_{{\rm{cr}}} $ 断裂应力 $ {\sigma }_{{\rm{R}}} $ /MPa峰值应力 $ {\sigma }_{{\rm{u}}} $ /MPa临界损伤值 $ {D}_{{\rm{cr}}} $ 1 273 0.163 0.256 77.3 115.3 0.33 0.161 0.250 96.4 139.7 0.31 1 373 0.143 0.263 39.3 63.4 0.38 0.168 0.257 63.1 97.0 0.35 1 473 0.131 0.257 25.9 45.6 0.43 0.153 0.251 42.4 70.7 0.40 1 573 0.123 0.252 20.4 38.4 0.47 0.143 0.246 30.8 55.1 0.44
下载: 导出CSV
-
[1] 刘永滨, 冯立德, 张季娜, 等. 天然气管道在役修补焊接过程中的数值模拟[J]. 焊接学报, 2019, 40(10): 111 − 115,120. Liu Yongbin, Feng Lide, Zhang Jina, et al. Numerical simulation on in-serve welding of natural gas pipeline[J]. Transactions of the China Welding Institution, 2019, 40(10): 111 − 115,120.
[2] 黄志强, 汤海平, 丁雅萍, 等. 天然气管道在役焊接温度场数值模拟[J]. 焊接学报, 2018, 39(6): 29 − 34. doi: 10.12073/j.hjxb.2018390143 Huang Zhiqiang, Tang Haiping, Ding Yaping, et al. Numerical simulation for in-service welding temperature field of gas pipeline[J]. Transactions of the China Welding Institution, 2018, 39(6): 29 − 34. doi: 10.12073/j.hjxb.2018390143
[3] Wu Q, Han T, Wang Y, et al. In-situ observation of high-temperature failure behavior of pipeline steel and investigation on burn-through mechanism during in-service welding[J]. Engineering Failure Analysis, 2019, 109(9): 104236.
[4] API 1104. Welding of pipelines and related facilities, appendix B: in service welding[S]. American petroleum institute, 2013.
[5] Cisilino A P, Chapetti M D, Ozegui J L, et al. Minimum thickness for circumferential sleeve repair fillet welds in corroded gas pipelines[J]. International Journal of Pressure Vessels and Piping, 2002(79): 67 − 76.
[6] Matthew A B, William A B, et al. The effect of hoop stress on the burn through susceptibility during in-service welding of thin-walled pipelines[C]. Canada: 2008 7th International Pipeline Conference, 2009.
[7] 郭广飞. X70钢高压气管线在役焊接烧穿判据研究[D]. 青岛: 中国石油大学(华东), 2014. Guo Guangfei. Study on burn-through criterion of X70 high-pressure gas pipeline during in-service welding[D]. Qingdao: China university of petroleum(East China), 2014.
[8] Wu Qian, Han Tao, Wang Hongtao, et al. Burn-through prediction during in-service welding based on residual strength and high-temperature plastic failure criterion[J]. International Journal of Pressure Vessels and Piping, 2021, 189(9): 104280.
[9] Majnoun P, Ghavi M R, Vakili-Tahami F, et al. A new thermo-mechanical approach to predict "burn-through" during the in-service welding[J]. International Journal of Pressure Vessels and Piping, 2021, 194(3): 104558.
[10] Lemaitre J A. Continuous damage mechanics model for ductile fracture[J]. Journal of Engineering Materials and Technology, 1985, 107(1): 10783.
[11] Oyane M. Criteria of ductile fracture strain[J]. Jsme International Journal, 2008, 15(90): 1507 − 1513.
[12] Bonora N, Gentile D, Pirondi A, et al. Ductile damage evolution under triaxial state of stress: theory and experiments[J]. International Journal of Plasticity, 2005, 21(5): 981 − 1007. doi: 10.1016/j.ijplas.2004.06.003
[13] Pirondi A, Bonora N. Modeling ductile damage under fully reversed cycling[J]. Computational Materials Science, 2003, 26(2): 129 − 141.
[14] 杨超众. 316LN钢热成形开裂预报与损伤规律研究[D]. 上海: 上海交通大学, 2014. Yang Chaozhong. Research on fracture and damage condition for 316LN steel during hot deformation[D]. Shanghai: Shanghai Jiao Tong University, 2014.
[15] Bonora N, Ruggiero A, Esposito L, et al. CDM modeling of ductile failure in ferritic steels: Assessment of the geometry transferability of model parameters[J]. International Journal of Plasticity, 2006, 22(11): 2015 − 2047. doi: 10.1016/j.ijplas.2006.03.013
[16] Lemaitre J, Desmorat R. Engineering damage mechanics : ductile, creep, fatigue and brittle failures[M]. Germany: Springer, 2005.
[17] Yang H, Li Z H, Zhang Z L, et al. Investigation on Zener-Hollomon parameter in the warm-hot deformation behavior of 20CrMnTi[J]. Journal of Zhejiang University-Science A(Applied Physics & Engineering), 2006, 7(8): 1453 − 1460.
[18] Mirzadeh H, Najafizadeh A. Flow stress prediction at hot working conditions[J]. Materials Science & Engineering A, 2010, 527(4-5): 1160 − 1164.
[19] Goldak J, Bibby M, Moore J, et al. Computer modeling of heat flow in welds[J]. Metallurgical Ttansactions B, 1986(17B): 587 − 600.
[20] Qian W, Yong W, Tao H, et al. Influence of internal corrosive defect on the burn-through of in-service welding on pipelines[J]. Journal of Pressure Vessel Technology, 2018, 140(4): 041701. doi: 10.1115/1.4039698
[21] Qian W, Yong W, Tao H, et al. Study on the failure mechanism of burn-through during in-service welding on gas pipelines[J]. Journal of Pressure Vessel Technology, 2019, 141(2): 024501. doi: 10.1115/1.4042461
计量
- 文章访问数: 271
- HTML全文浏览量: 27
- PDF下载量: 36
