Finite element analysis of solder joint reliability of 3D packaging chip
-
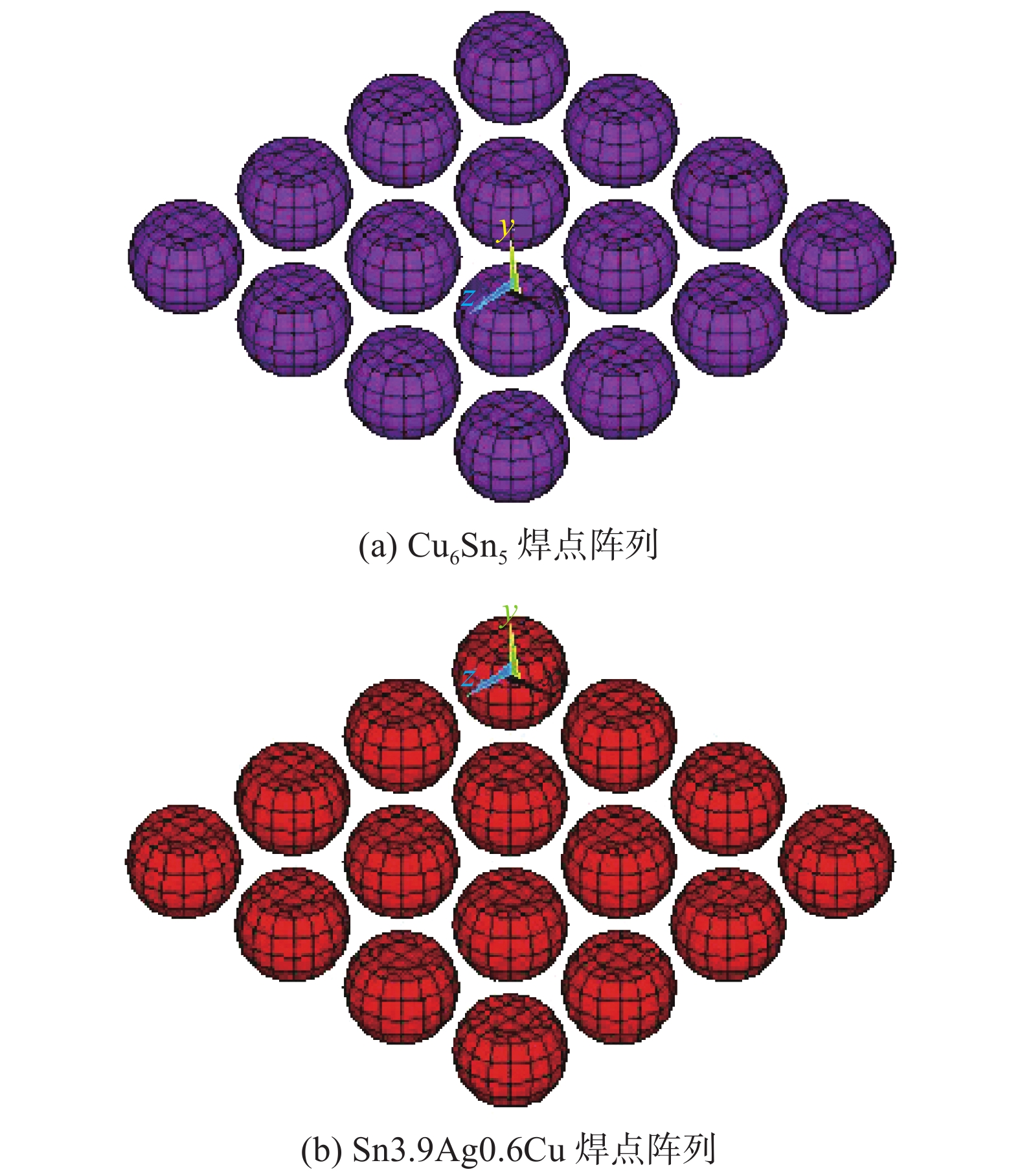
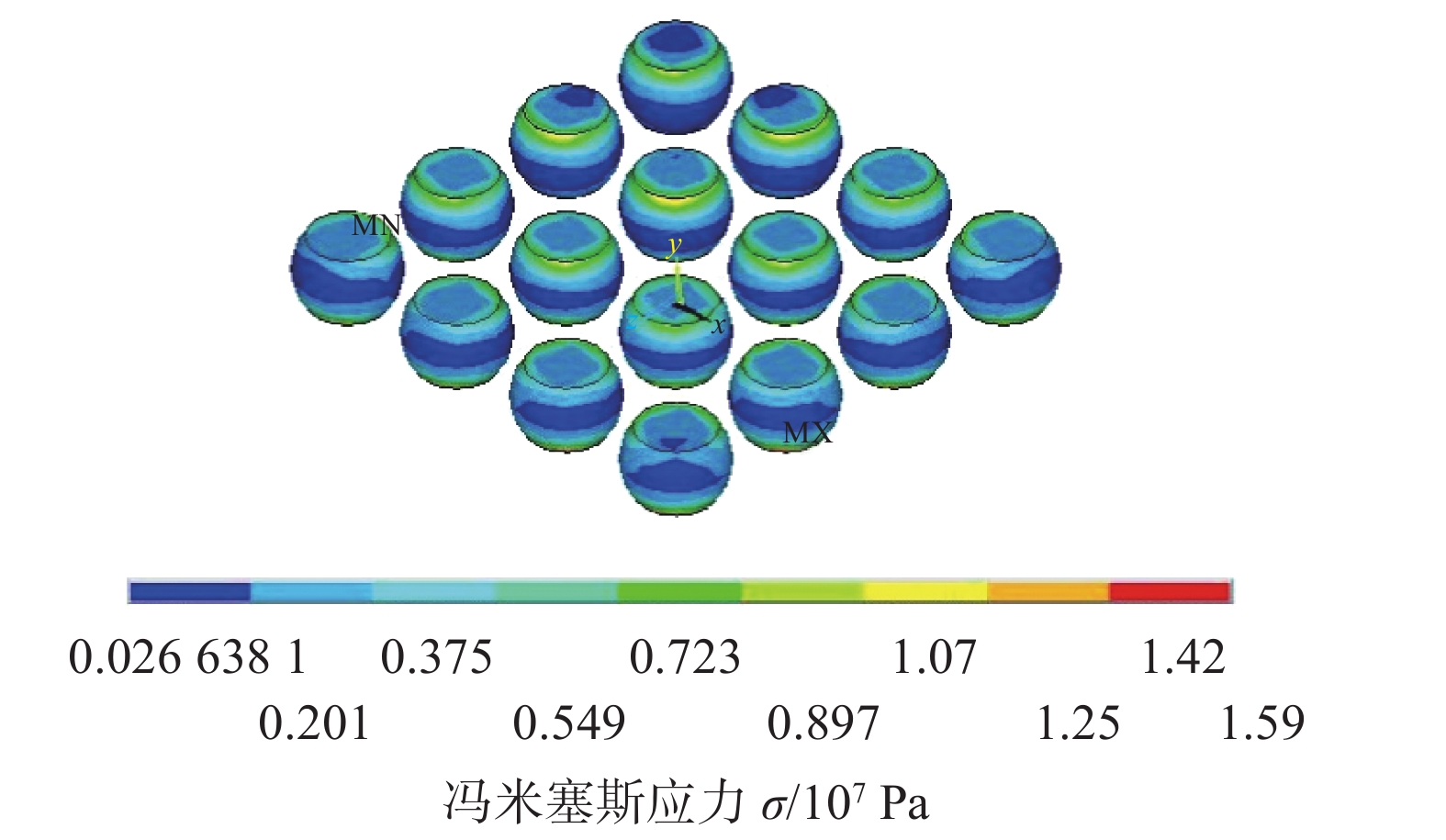
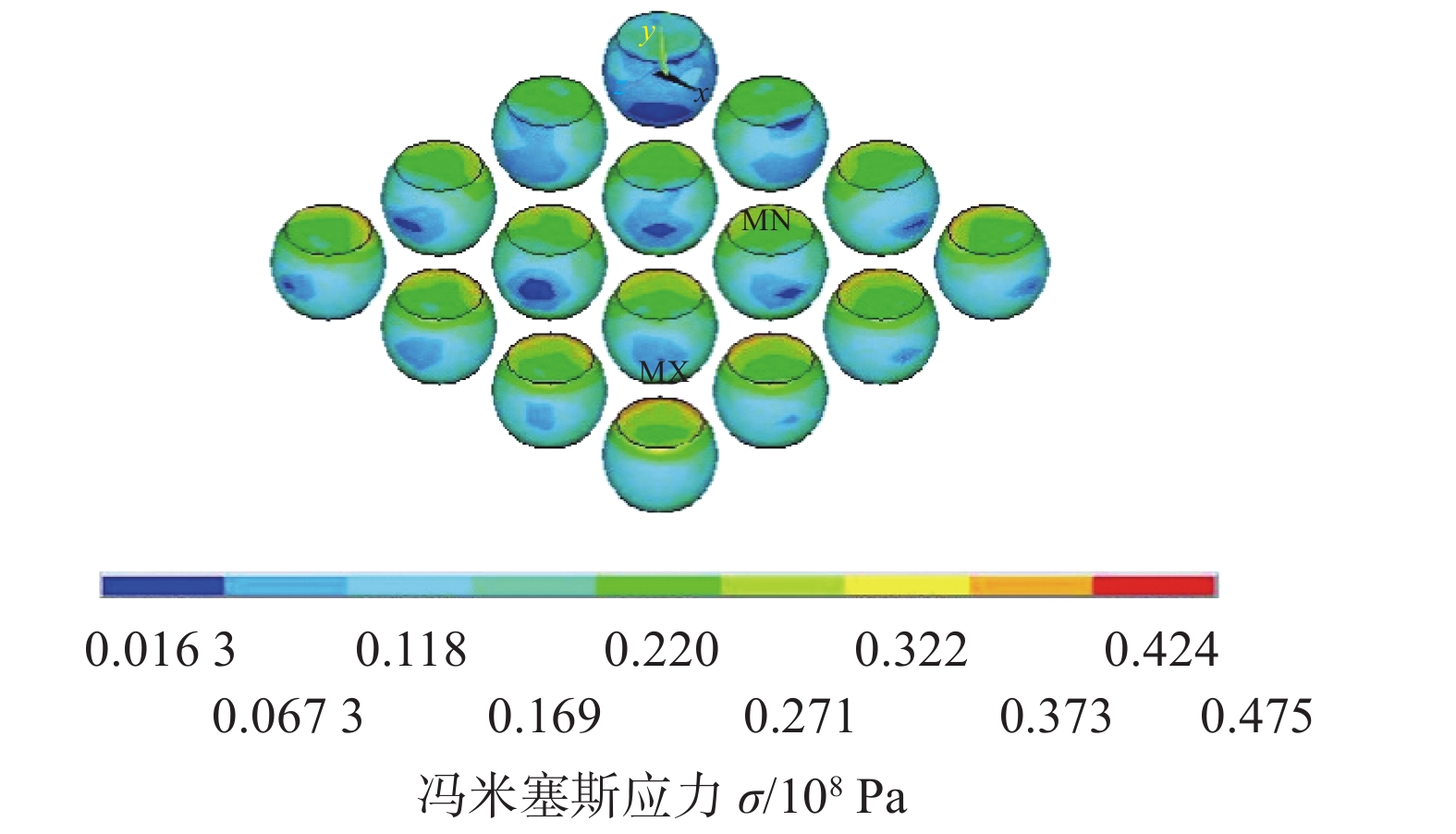
摘要: 选择工业中广泛使用的Sn,Sn3.9Ag0.6Cu钎料作为三维封装芯片键合焊点材料,采用ANSYS有限元软件建立三维封装模型,基于Garofalo-Arrhenius本构方程,进行−55 ~ 125 °C热循环模拟,并通过田口法探讨封装结构和工艺参数对焊点的可靠性影响. 结果表明,Cu柱与焊点接触处是整个结构的薄弱区域,在IMC焊点阵列中最右列第二个焊点处出现最大应力. 通过田口法,结合有限元模拟结果,获得了4个因子对S/N的贡献度由大到小依次为:焊点阵列、焊点高度、芯片厚度、焊点材料. 其中焊点阵列的影响最大,其次是焊点高度、芯片厚度,焊点材料影响最小. 基于优化设计,获得了最优的匹配组合为3 × 3阵列,焊点高度0.02 mm,芯片厚度0.2 mm,焊点材料Cu6Sn5.Abstract: In this paper, Sn and Sn3.9Ag0.6Cu solders, which are widely used in industry, were selected as bonding materials for 3D packaging chips. The 3D packaging model was established using ANSYS finite element software. Based on the Garofalo-Arminius’s constitutive equation, the process of thermal cycle under the temperature condition from −55 ~ 125 °C. In addition, the influence of packaging structure and process parameters on the reliability of solder joint was discussed by Taguchi method. The results show that the contact area between Cu pillar and solder joint is the weak area of the whole structure, and the maximum stress appears at the second solder joint in the rightmost row of the intermetallic compound (IMC) solder joint array. Through the Taguchi method and combined with the finite element simulation results, the contribution of the four factors to S/N was obtained as follows: solder joint array, solder joint height, chip thickness, solder joint material, of which the solder joint array has the largest influence, followed by solder joint height and chip thickness, solder joint material has the least influence. Based on the optimization design, the optimal matching combination was solder joint array 3 × 3, solder joint height 0.02 mm, chip thickness 0.2 mm and solder joint material Cu6Sn5.
-
Keywords:
- 3D packaging /
- reliability of solder joint /
- stress distribution /
- Taguchi method
-
0. 序言
焊接技术是工业热工艺加工当中使用率较高的技术之一,在实际工业中,由于材料本身和外部环境等问题,会在焊接部位形成不同程度的缺陷,如未熔合、裂纹等[1],拥有可靠的焊缝缺陷检测技术对保证工艺质量具有重大意义. 在传统的焊缝图像缺陷检测工作中,主要以人工检测X射线焊缝图像为主[2],由于焊缝缺陷形成复杂,且易受检测人员主观判断影响,给检测工作带来很大困难[3]. 随着智能技术的推进,深度学习模型在焊缝缺陷检测领域表现突飞猛进,卷积神经网络通过反向传播学习目标特征,可以有效解决X射线焊缝缺陷检测问题. 国内外学者就此问题进行了研究,Xu等人[4]基于卷积神经网络的迁移学习,研究设计域间异构迁移学习方法,对焊缝缺陷检测进行探索. Liang 等人[5]采用卷积注意力模块,提出跨模态注意关注焊缝图像的关键区域,提高了焊缝缺陷检测的精度.Razfar等人[6]使生成对抗网络和深度卷积神经网络结合,提高了低对比度的焊缝图像检测效果.但上述几种模型参数量大、浮点运算多,在提升检测精度的同时增大了计算量,造成了成本高、检测速度低和实用性较差等棘手难题.
在实际生产中,由于需要更快速地处理数据,避免与远程服务器交换不可靠的数据,大多应用需要在靠近数据源的边缘设备上本地部署模型,性能与成本也因此受到限制. 高性能模型成本极高,快速检测的轻量级模型又伴随一定精度损失,越来越多的学者对于模型轻量化的问题进行研究. Liu等人[7]设计了高效特征提取模块,低成本处理输入数据,提升了网络在焊缝缺陷检测工作中的工业实用性.Zhu等人[8]改进了RenNet网络从而实现模型轻量化,结合注意力机制和边界抗混叠模块,获得了不错的焊缝缺陷检测速度.Yang等人[9]提出一个小尺寸预训练SqueezeNet模型,并将其部署到树莓派嵌入式系统中,响应时间缩短. 上述模型实现了参数量下降、检测速度上升,但是检测精度也因未全面学习缺陷特征而下降,现阶段模型仍存在难以合理平衡精度和检测速度的问题.
针对平衡精度和检测速度的问题,本文优先从网络轻量化入手,搭建新型主干网络,降低模型深度,设计超轻量卷积方式,使用Depthwise卷积用更少代价生成更多有效冗余特征映射,减少模型参数量和浮点运算数,实现网络轻量化. 模型轻量化伴随精度损失是由于焊缝缺陷分布散乱的特征和部分缺陷种类成像间断导致未全面学习缺陷特征所致,适当的跨通道交互可以在显著降低模型复杂度的同时保持性能.因此,设计高效轻量级专注模块,从水平和垂直两个方向捕获孤立区域关系,结合轻量级上采样算子,使模型特征重组时具有较大感受野,更好地利用周围信息,弥补网络轻量化造成的精度损失. 最后,设计OS-IoU损失函数,提高损失函数效率,强化距离损失和形状损失关注程度,重新定义惩罚项及相关性,提高模型预测精度. 总之,本文采用先轻量化后弥补精度损失的方案,提出了一种轻量级高效X射线焊缝图像缺陷检测方法(LHODM),对X射线焊缝缺陷检测工作的相关研究及实际应用具有一定的指导意义.
1. 试验方法
文中设计的LHODM模型结构如图1所示,依据参考文献[10]的YOLOv5s网络架构设计新型主干网络,如图1(a)所示,由1个常规卷积与4个ULConv卷积组成,该操作有效降低了模型深度和模型参数量,方便模型在嵌入式设备终端部署,完成焊缝检测工作. 通过对比深度神经网络提取特征图发现存在较多相似特征图,而丰富甚至冗余的特征信息通常可以保证网络对输入的全面理解. 由此设计ULConv卷积,使用廉价操作生成更多特征映射,缓解生成相似特征的卷积带来的参数量增加问题,降低计算成本,同时充分揭示内在特征背后信息. 图1中的ULConv结构由Lweightconv和C3Lweight组成,其中核心组件Lweight由常规卷积生成不含冗余的特征图1,再由特征图1通过Depthwise卷积生成特征图2[11],Depthwise卷积中卷积核只与一个特征通道卷积,改变特征图大小而不改变通道数,缩减卷积成本,最后将特征图1和特征图2拼接. 改进后的卷积方式参数量大幅减少,降低了模型对内存和计算资源的需求.
模型轻量化会带来精度损失的问题,为弥补精度损失,考虑到适当的跨通道交互可以显著降低模型复杂度的同时保持性能,设计高效轻量化专注模块ELCC,该模块只涉及少量参数,结构如图2所示. 由于焊缝缺陷具有分布散乱且缺陷不连通特点,对于维度为W × H × C的输入特征图,通过条纹池化将输入特征图分别进行水平条纹池化处理和垂直条纹池化处理,得到双方向上的对应单列池化特征,分别使用一个1D卷积,将单列池化特征进行同方向扩展,最后将水平方向的条纹池化扩展图与垂直方向的条纹池化扩展图进行融合. 经过一个1 × 1卷积和Sigmoid层,与原输入进行对应元素相乘,得到最终输出. 完成对空间信息进行压缩操作后,获得1 × 1 × C的中间特征图. 对压缩后特征图,使用自适应动态卷积核做1 × 1卷积进行通道特征学习,学习不同通道之间的重要性.
学习完成后将通道注意力特征图和原始输入特征图进行通道相乘,最终输出具有通道专注的特征图. 条纹池化可以捕获孤立区域的长距离关系,在空间维度上保持较窄的内核形状,便于捕捉局部上下文信息,防止无关区域干扰标签预测,ELCC模块的设计,不仅响应轻量化需求,还有效缓解主干网络轻量化带来的精度损失问题.
传统上采样具有诸多不足,如最近邻上采样和双线性上采样仅通过像素点空间位置来决定上采样核[12-13],没有利用到语义信息,且感知域很小,如文献[14]的Deconvolution,对于特征图每个位置都是应用相同上采样核,不能捕捉到特征图内容信息,且引入了大量参数和计算量. 理想上采样应具有较大感受野,可以更好地利用周围信息,具备轻量化特点且和特征图语义信息相关. CARAFE算子首先利用输入特征图来预测上采样核,每个位置上采样核均不相同,基于预测的上采样核进行特征重组. 同时,CARAFE参数量低、运算量小,响应轻量化需求. CARAFE分为两个模块,分别是上采样核预测模块和特征重组模块,结构如图3所示. 上采样核预测模块,对于形状为H × W × C的输入特征图,使用一个1 × 1卷积将通道数压缩到Cm,该步骤是为了减少后续计算量. 对压缩后的输入特征图,使用卷积预测上采样核,输入通道数为Cm,随后将通道维在空间维展开,得到新上采样核,最后利用softmax方法进行归一化,使卷积核权重和为1. 特征重组模块,对于输出特征图中全部位置,将其映射回输入特征图,取出以之为中心的Kup × Kup区域与预测出该点上采样核做点积运算,得到输出值,相同位置的不同通道共享用一个上采样核[15].
传统边界框损失函数CIoU,并没有考虑真实框和预测框之间的方向,导致模型收敛速度缓慢或无法有效收敛. 为进一步考虑真实框和预测框之间的向量角度,本文设计OS-IoU损失函数如图4所示,重新定义惩罚项及其相关性,考虑期望回归向量之间的夹角,强化距离损失和形状损失关注程度. OS-IoU损失函数包含4个部分,分别为角度损失、距离损失、形状损失和IoU损失. OS-IoU角度损失 $ \varLambda $的示意图如图4(a)所示,公式为
$$ \varLambda=1-2 \times \sin ^{2}\left(\arcsin \left(\frac{c_{{\rm{h}}}}{\sigma}\right)-\frac{\text{π}}{4}\right) $$ (1) $$ \varLambda=\cos \left(2 \times\left(\arcsin \left(\frac{c_{\rm{h}}}{\sigma}\right)-\frac{\text{π}}{4}\right)\right) $$ (2) $$ c_{{\rm{h}}}=\max \left(b_{{\rm{c}}_{{\rm{y}}}}^{{\rm{g t}}}, b_{{\rm{c}}_{{\rm{y}}}}\right)-\min \left(b_{{\rm{c}}_{{\rm{y}}}}^{{\rm{g t}}}, b_{{\rm{c}}_{{\rm{y}}}}\right) $$ (3) $$ \sigma=\sqrt{\left(b_{{\rm{c}}_{{\rm{x}}}}^{{\rm{g t}}}-b_{{\rm{c}}_{{\rm{x}}}}\right)^{2} + \left(b_{{\rm{c}}_{{\rm{y}}}}^{{\rm{g t}}}-b_{{\rm{c}}_{{\rm{y}}}}\right)^{2}} $$ (4) 式中:$ \sigma $为真实框和预测框中心点距离;$ c_{{\rm{h}}} $为真实框和预测框中心点的高度差;($ b_{{\rm{c}}_{{\rm{x}}}}^{{\rm{g t}}} $,$ b_{{\rm{c}}_{{\rm{y}}}}^{{\rm{g t}}} $)为真实框中心坐标;($ b_{{\rm{c}}_{{\rm{x}}}} $,$ b_{{\rm{c}}_{{\rm{y}}}} $)为预测框中心坐标.
OS-IoU距离损失$ \varDelta $的示意图如图4(b)所示,公式为
$$ \varDelta = \sum\limits_{t = x,y} {(1 - {e^{ - \gamma {\rho _{\rm{t}}}}}) = 2 - {e^{ - \gamma {\rho _{\rm{x}}}}} - {e^{ - \gamma {\rho _{\rm{y}}}}}} $$ (5) $$ {\rho _{\rm{x}}} = {\left(\frac{{ b_{{\rm{c}}_{{\rm{x}}}}^{{\rm{g t}}} - {b_{{{\rm{c}}_{\rm{x}}}}}}}{{{c_{\rm{w}}}}}\right)^2} $$ (6) $$ {\rho _{\rm{y}}} = {\left(\frac{{ b_{{\rm{c}}_{{\rm{y}}}}^{{\rm{g t}}} - {b_{{{\rm{c}}_{\rm{y}}}}}}}{{{c_{\rm{h}}}}}\right)^2} $$ (7) $$ \gamma = 2 - \varLambda $$ (8) 式中:$ c_{{\rm{w}}} $为真实框和预测框最小外接矩形的宽;$\gamma $,${\rho _{\rm{x}}} $,${\rho _{\rm{y}}} $为公式的中间量.
OS-IoU形状损失$\varOmega$的公式为
$$ \varOmega = {(1 - {e^{ - {w_w}}})^\theta } + {(1 - {e^{ - {w_h}}})^\theta } $$ (9) $$ \varOmega = {\sum\limits_{t = w,h} {(1 - {e^{ - wt}})} ^\theta } $$ (10) $$ {w_w} = \frac{{\left| {w - {w^{{\rm{gt}}}}} \right|}}{{\max (w,{w^{{\rm{gt}}}})}} $$ (11) $$ {w_h} = \frac{{\left| {h - {h^{{\rm{gt}}}}} \right|}}{{\max (h,{h^{{\rm{gt}}}})}} $$ (12) 式中:$ w $为预测框的宽;$ h $为预测框的高,;$ {w^{{\rm{gt}}}} $为真实框的宽;$ {h^{{\rm{gt}}}} $为真实框的高;$ \theta $控制对形状损失的关注程度.
OS-IoU损失函数中IoU损失$ \varPsi $如图4(c)所示,公式为
$$ \varPsi = \frac{{\left| {A \cap B} \right|}}{{\left| {A \cup B} \right|}} $$ (13) 式中:A为物体真实边框;B为预测边框.
OS-IoU损失函数的定义为
$$ L_{{\rm{OS-IoU}}}=1-\varPsi + \frac{2(\varDelta + \varOmega )}{3} $$ (14) LHODM网络损失函数由矩形框损失函数$ {L_{\rm{r}}} $、目标置信度损失函数$ {L_{\text{o}}} $、目标分类概率损失函数$ {L_{\rm{c}}} $组成. 网络中矩形框损失函数采用OS-IoU,目标置信度损失、目标分类概率损失采用二分类交叉熵损失(binary cross entropy loss,BCE)[16],损失函数L公式为
$$ {L_B} = - \frac{1}{j}\sum\limits_j {\left[ {k\ln c + (1 - k)\ln (1 - c)} \right]} $$ (15) $$ L= n\times {L_{\rm{r}}} + m\times {L_{\rm{o}}} + r\times {L_{\rm{c}}} $$ (16) $$ n + m + r = 1 $$ (17) 式中:LB为二分类交叉熵损失;$ k $为目标信息;$ c $为预测输出信息;$ j $为样本总量;$ n $,$ m $,$ r $分别为$ {L}_{{\rm{r}}}, {L}_{{\rm{o}}},{L}_{{\rm{c}}} $3大损失加权和,且权重和为1.
2. 试验准备
2.1 数据集
在实际工业中,X射线焊缝常见缺陷分为内部缺陷和外部缺陷. 常见缺陷有夹渣(s)、咬边(u)、裂纹(c)、气孔(p)、未焊透(lop)、未熔合(lof). 文中采用的数据集是由中国石油天然气管道科学研究院和GDXray公共数据库提供的缺陷底片样本共同组成[17],由于焊缝图像尺寸不协调,长宽比过大,遂使用先验知识对现有数据集图像进行裁剪,共获得尺寸大小为160 × 160像素的缺陷图像2 647张,其中涉及缺陷分别为裂纹缺陷图像486张、未熔合缺陷图像498张、未焊透缺陷图像482张、气孔缺陷图像502张、夹渣缺陷图像499张、咬边缺陷图像180张. 为方便后续模型训练,提前将图像划分为训练集、验证集和测试集,划分比例为7∶2∶1,最终得到训练集图像1851张、验证集图像527张、测试集图像269张.
2.2 试验环境
试验基于 Windows64位操作系统,硬件配置为:中央处理器(CPU)为AMD Ryzen 7 5800H with Radeon Graphics,显卡使用NVIDIA GeForce RTX 3060 Laptop GPU,在Pytorch框架下进行. 初始学习率设置为 0.001,迭代300次,Batch-size大小为64.
2.3 性能指标
为客观、有效地对模型性能及改进模型效果进行评价,文中使用评价指标为准确率P、召回率R、均值平均精度PA0.5、参数量PM和每秒传输帧数FPS.其中准确率P表示预测为真的样本中正样本数所占整个样本比例,召回率R表示在所有真实情况为正的样本中预测为真的样本数所占比例. 平均精度PA是不同召回率下准确率的平均值,均值平均精度$\overline P_{\rm{A}}$表示不同类别的PA值的平均值. PA0.5表示IOU设置为0.5时,计算每个类别的PA均值. 具体公式为
$$ P = \frac{{P_{\rm{T}}}}{{P_{\rm{T}} + P_{\rm{F}}}} $$ (18) $$ R = \frac{{P_{\rm{T}}}}{{P_{\rm{T}} + N_{\rm{F}}}} $$ (19) $$ \overline P_{\rm{A}} = \frac{1}{q}\sum\limits_{i = 1}^q {P_{{\rm{A}}i}} $$ (20) 式中:PT表示预测为真的正样本;NF表示预测为假的负样本;PF表示预测为假的正样本;q表示类别数;PAi表示第i个类别的PA值[18].
3. 试验结果与分析
3.1 模型训练结果
图5为LHODM模型训练曲线,其中包括F1-C,P-C,R-C,P-R曲线. F1-C曲线是精确率和召回率的调和平均值,一般来说,置信度阈值较低时,较多置信度低的样本会被认为真,召回率高,精确率低;相反置信度阈值较高时,置信度高的样本才能被认为是真,检测结果就会越准确;P-C曲线,当置信度越大时,类别检测越准确;R-C曲线,当置信度越小时,类别检测越全面;P-R曲线体现精确率和召回率的关系,通常希望在准确率很高的前提下,尽可能地找到全部缺陷类别,因此曲线面积越接近1,模型效果越好. 整体来看,模型训练结果良好,在保证一定准确率的前提下,可实现对缺陷类别的全面识别. 由模型训练结果来看,训练300轮次后,各项曲线基本收敛,$\overline P_{\rm{A}} $值已收敛,达到稳定状态,通常认为可以结束训练并获取模型权重.
3.2 对比试验结果
为证明文中模型性能平衡且检测表现优异,选择主流一阶段、二阶段目标检测网络和LHODM进行对比,对比模型分别为YOLOv5s,CentripetalNet,Faster-RCNN,Cascade-RCNN,YOLOv3,LHODM模型检测结果[19-22]. 图6为在GDXray数据集与中国石油天然气管道科学研究院提供的X射线焊缝数据集随机选择的4张图象上的模型检测结果,方框表示缺陷存在位置并标明缺陷类别与置信度. 由检测结果可知,CentripetalNet,Faster-RCNN,YOLOv3,Cascade-RCNN4种模型均出现不同程度的漏检现象且缺陷置信度较低,在实际工业中,4种模型均无法达到工业需求.
LHODM模型具有较大检测优势,与YOLOv5s模型相比,LHODM同样可识别漏检缺陷,可检测部分遮挡缺陷或成像不明显缺陷,虽然缺陷置信度有微弱下降,但对实际检测结果没有影响. 在牺牲极少精度损失的前提下,获得明显速度提升、参数量减少回报,降低成本,对X射线焊缝检测工作来说,是综合性能提升的表现.
在实际检测结果对比试验中,LHODM具有良好的检测效果. 为更全面评价模型,设计了$\overline P_{\rm{A}} $值、参数量、测试时间、FPS性能指标测试试验,试验结果如表1所示.
表 1 模型性能对比Table 1. Model performance comparison模型 均值平均精度
PA0.5参数量
PM/M测试时间
t/ms每秒传输帧数FPS/
(帧·s−1)YOLOv5s 92.04 7.03 23.47 42.61 YOLOv3 91.33 61.54 190.48 5.25 Faster-RCNN 89.67 41.14 158.73 6.30 Cascade-RCNN 90.46 68.94 126.90 7.88 CentripetalNet 88.19 205.68 127.06 7.87 LHODM 91.62 3.99 15.76 63.47 试验结果表明,LHODM以降低0.42%$\overline P_{\rm{A}} $值为代价,检测速度提升了20.86帧/s,参数量下降了3.04 M,测试时间缩短了7.71 ms,综合性能显著提升. LHODM降低了对内存和硬件需求,实用性更佳.
3.3 消融试验结果
为验证文中各方法的有效性设计了相关消融试验,由于参考了YOLOv5s网络架构,故在YOLOv5s网络架构中进行本文提出设计的验证工作,试验结果如表2所示. 其中包括替换YOLOv5s卷积方式为ULConv卷积,试验结果表明,网络参数量由7.03 M降低至3.69 M,检测速度由42.61帧/s提高至65.33帧/s,模型计算复杂度和空间复杂度降低,网络明显轻量化,但同时$\overline P_{\rm{A}} $值由92.04%降低至88.46%,可见模型轻量化设计带来一定程度的精度损失. 为弥补由模型轻量化造成的精度损失问题,本文采取两种措施,分别是使用轻量级上采样算子CARAFE和设计轻量级高效专注模块ELCC,将两个模块应用到YOLOv5s进行消融试验,结果表明,CARAFE算子使得模型参数量增长了0.16 M,$\overline P_{\rm{A}} $值提升了0.29%;ELCC模块使参数量增长了0.17 M,$\overline P_{\rm{A}} $值提升0.36%. 由此可知,CARAFE算子与ELCC模块在带来参数量小幅增长的同时,可带来更大精度回报. 同时结合焊缝缺陷特点,考虑模型受到真实框和预测框之间的方向影响,设计OS-IoU损失函数替换YOLOv5s的CIoU损失函数,试验结果表明,在模型参数量不变的前提下$\overline P_{\rm{A}} $值由92.04%提升至92.19%.
表 2 LHODM模块消融结果Table 2. Module ablation results of LHODM模型 准确率P(%) 召回率R(%) 均值平均精度PA0.5 参数量PM/M 测试时间t/ms 每秒传输帧数FPS/(帧·s−1) YOLOv5s 90.17 87.36 92.04 7.03 23.47 42.61 YOLOv5s + ULConv 85.52 83.15 88.46 3.69 15.31 65.33 YOLOv5s + CARAFE 91.39 88.44 92.33 7.20 25.58 39.09 YOLOv5s + L-ELCC 89.77 88.01 92.41 7.21 25.54 39.16 YOLOv5s + OS-IoU 89.21 87.58 92.19 7.03 23.47 42.61 YOLOv5s + ULConv + CARAFE 85.76 83.20 88.73 3.86 17.94 55.74 YOLOv5s + ULConv + CARAFE + ELCC 86.32 84.67 89.70 3.99 15.76 63.47 LHODM 89.98 87.79 91.62 3.99 15.76 63.47 综上所述,使用ULConv卷积组成的主干网络可实现模型轻量化,CARAFE与ELCC可弥补精度损失,OS-IoU可提升模型精度. 为进一步验证4种方法结合使用效果,在YOLOv5s框架上先后叠加使用上采样算子CARAFE,ULConv,ELCC和OS-IoU损失函数,试验结果表明,LHODM综合性能显著提升,拥有轻量化网络和不错的精度表现.
4. 结论
(1)参考深度学习YOLOv5s模型原始框架的基础上,重新设计主干网络,提出轻量级卷积ULConv,使用Depthwise操作生成更多有效冗余特征,丰富的特征信息通常可以保证网络对输入的全面理解.
(2)设计ELCC高效轻量化专注模块,使用条纹池化捕获孤立区域的长距离关系,在空间维度上保持较窄的内核形状,便于捕捉局部上下文信息,防止无关区域干扰标签预测.
(3)结合轻量级上采样算子CARAFE,在响应模型轻量化前提下,加强整体通道特征,使网络更加关注待检测目标,在模型特征重组时具有更大感受野,更有效利用环境周围信息. 最后,设计符合焊缝缺陷特点的OS-IoU损失函数,考虑期望回归向量之间的夹角,重新定义惩罚项及相关性,构建LHODM网络.
-
表 1 材料参数
Table 1 Materials parameters
材料 弹性模量E/GPa 泊松比γ 热膨胀系数α/10−6K−1 屈服强度ReL/GPa 切变模量G/GPa 芯片 163 0.28 2.5 Cu柱 117 0.35 14.3 Cu6Sn5 124 0.30 19.0 1.86 50.4 Sn3.9Ag0.6Cu 74.84 0.30 16.6 BT基板 26 0.39 15.0 表 2 材料蠕变参数
Table 2 Creep parameters of materials
C1/s−1 C2/10−9Pa−1 C3 C4/K 441000 5 4.2 5412 表 3 控制因子和水平
Table 3 Control factors and levels
控制因子 水平1 水平2 水平3 焊点材料A Sn3.9Ag0.6Cu Cu6Sn5 Cu3Sn 焊点阵列B 5 × 5 4 × 4 3 × 3 焊点高度C 0.08 mm 0.04 mm 0.02 mm 芯片厚度D 0.2 mm 0.1 mm 0.05 mm 表 4 田口正交试验方案
Table 4 Taguchi orthogonal test
试验 因子与水平 评价指标 S/N A B C D Δσ/GPa 1 1 1 1 1 0.055 8 25.07 2 1 2 2 2 0.047 5 26.47 3 1 3 3 3 0.041 0 27.74 4 2 1 2 3 0.056 2 25.00 5 2 2 3 1 0.044 7 26.99 6 2 3 1 2 0.015 9 27.33 7 3 1 3 2 0.057 1 24.87 8 3 2 1 3 0.051 4 25.78 9 3 3 2 1 0.017 8 27.70 平均值 26.33 表 5 信噪比S/N平均效应响应
Table 5 Average effect response for S/N ratio
水平 A B C D 水平1 26.43 24.98 26.06 26.59 水平2 26.44 26.41 26.39 26.22 水平3 26.11 27.59 26.53 26.17 效应 0.33 2.61 0.47 0.42 排名 4 1 2 3 -
[1] Sun L, Chen M H, Zhang L, et al. Recent progress in SLID bonding in novel 3D-IC technologies[J]. Journal of Alloys and Compounds, 2020, 818: 152825. doi: 10.1016/j.jallcom.2019.152825
[2] Hang C J, Tian Y H, Zhang R, et al. Phase transformation and grain orientation of Cu-Sn intermetallic compounds during low temperature bonding process[J]. Journal of Materials Science: Materials in Electronics, 2013, 24(10): 3905 − 3913. doi: 10.1007/s10854-013-1337-5
[3] 吕亚平, 刘孝刚, 陈明祥, 等. 含TSV结构的3D封装多层堆叠Cu/Sn键合技术[J]. 先进封装技术, 2014, 39(1): 64 − 70. Lü Yaping, Liu Xiaogang, Chen Mingxiang, et al. Multilayer stack Cu/Sn bonding technology for 3D packaging with TSV[J]. Advanced Packaging Technologies, 2014, 39(1): 64 − 70.
[4] 张亮, 韩继光, 郭永环, 等. WLCSP器件Sn3.9Ag0.6Cu焊点疲劳寿命预测[J]. 焊接学报, 2012, 33(3): 97 − 100. Zhang Liang, Han Jiguang, Guo Yonghuan, et al. Fatigue life prediction of Sn3.9Ag0.6Cu-soldered joints in WLCSP device[J]. Transactions of the China Welding Institution, 2012, 33(3): 97 − 100.
[5] 田艳红, 王宁, 杨东升, 等. 三维封装芯片键合IMC焊点应力分析及结构优化[J]. 焊接学报, 2012, 33(8): 17 − 20. Tian Yanhong, Wang Ning, Yang Dongsheng, et al. Stress analysis and structure optimization of IMC joints in 3D package[J]. Transactions of the China Welding Institution, 2012, 33(8): 17 − 20.
[6] 邵良滨, 黄春跃, 梁颖, 等. 基于热-结构耦合的叠层金凸点应力分析[J]. 焊接学报, 2017, 38(1): 31 − 34. Shao Liangbin, Huang Chunyue, Liang Ying, et al. Study on stacked AU bumps stress based on thermal-structure coupling[J]. Transactions of the China Welding Institution, 2017, 38(1): 31 − 34.
[7] 陈照辉. 大功率LED封装和硅通孔三维封装工艺及可靠性数值仿真与试验研究[D]. 上海: 上海交通大学, 2012. Chen Zhaohui. Study on process and reliability of high power LED packaging and through silicon via 3D packaging by simulation and experiment[D]. Shanghai: Shanghai Jiao Tong University, 2012.
[8] 韩立帅, 黄春跃, 梁颖, 等. 3D封装微尺度CSP焊点随机振动应力应变分析[J]. 焊接学报, 2019, 40(6): 64 − 70. doi: 10.12073/j.hjxb.2019400156 Han Lishuai, Huang Chunyue, Liang Ying, et al. Analysis of stress strain and shape size optimization of 3D micro-scale CSP solder joints in random vibration[J]. Transactions of the China Welding Institution, 2019, 40(6): 64 − 70. doi: 10.12073/j.hjxb.2019400156
[9] Annuar S, Mahmoodian R, Hamdi M, et al. Intermetallic compounds in 3D integrated circuits technology: a brief review[J]. Science and Technology of Advanced Materials, 2017, 18(1): 693 − 703. doi: 10.1080/14686996.2017.1364975
[10] Lall P, Islam M N, Singh N, et al. Model for BGA and CSP reliability in automotive underhood applications[J]. IEEE Transactions on Components and Packaging Technologies, 2004, 27(3): 585 − 593. doi: 10.1109/TCAPT.2004.831824
[11] 梁颖, 黄春跃, 黄伟, 等. 基于正交设计的WLCSP柔性无铅焊点随机激励应力应变分析[J]. 焊接学报, 2016, 37(2): 13 − 16. Liang Ying, Huang Chunyue, Huang Wei, et al. Stress and strain distribution of lead-free solder joints with compliant layer in wafer level chip scale package under random vibration based on orthogonal design[J]. Transactions of the China Welding Institution, 2016, 37(2): 13 − 16.
[12] 胡丹, 沈骏, 陈旭, 等. 正弦振动引起的BGA焊点Sn-Cu金属间化合物失效机理[J]. 中国有色金属学报, 2019, 29(4): 756 − 763. Hu Dan, Shen Jun, Chen Xu, et al. Fracture mechanism of Sn-Cu intermetallic compound layer in BGA solder joint induced by sinusoidal vibration[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(4): 756 − 763.
[13] 张亮, 韩继光, 郭永环, 等. WLCSP器件结构优化模拟及无铅焊点可靠性[J]. 焊接学报, 2012, 33(7): 53 − 56. Zhang Liang, Han Jiguang, Guo Yonghuan, et al. Optimum simulation and soldered joints reliability of WLCSP device[J]. Transactions of the China Welding Institution, 2012, 33(7): 53 − 56.
[14] Zhang L, Han J G, Guo Y H, et al. Anand model and FEM analysis of SnAgCuZn lead-free solder joints in Wafer Level Chip Scale Packaging devices[J]. Microelectronics Reliability, 2014, 54(1): 281 − 286. doi: 10.1016/j.microrel.2013.07.100
[15] Samavatian M, Samavation V, Moayeri M, et al. Effect of stress triaxiality on damage evolution of porous solder joints in IGBT discretes[J]. Journal of Manufacturing Processes, 2018, 32: 57 − 64. doi: 10.1016/j.jmapro.2018.01.025
[16] Wu K C, Lin S Y, Hung T Y, et al. Reliability assessment of packaging solder joints under different thermal cycle loading rates[J]. IEEE Transactions on Device and Materials Reliability, 2015, 15(3): 437 − 442. doi: 10.1109/TDMR.2015.2462726
[17] Zhang L, Sun L, Guo Y H, et al. Reliability of lead-free solder joints in CSP device under thermal cycling[J]. Journal of Materials Science: Materials in Electronics, 2014, 25: 1209 − 1213. doi: 10.1007/s10854-014-1711-y
[18] Ladani L J. Stress analysis of 3-dimensional IC package as function of structural design parameters[J]. Microelectronic Engineering, 2010, 87(10): 1852 − 1860. doi: 10.1016/j.mee.2009.11.002
[19] Li M H C, Hong S M. Optimal parameter design for chip-on-film technology using the Taguchi method[J]. The International Journal of Advanced Manufacturing Technology, 2005, 25(1−2): 145 − 153. doi: 10.1007/s00170-003-1824-6
[20] Tsai T N, Liukkonen M. Robust parameter design for the micro-BGA stencil printing process using a fuzzy logic-based Taguchi method[J]. Applied Soft Computing, 2016, 48: 124 − 136. doi: 10.1016/j.asoc.2016.06.020
[21] Mertol A. Application of the Taguchi method on the robust design of molded 225 plastic ball grid array packages[J]. IEEE Transactions on Components, Packaging, and Manufacturing Technology, 1995, 18(4): 734 − 743. doi: 10.1109/96.475283




 下载:
下载: