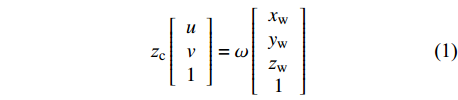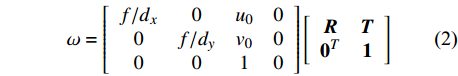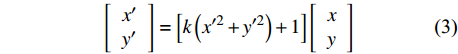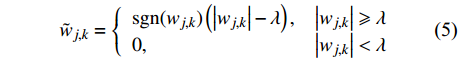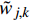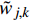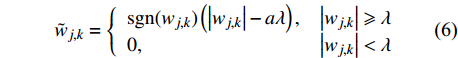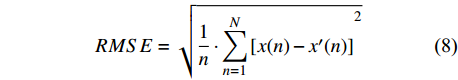Study on soft-hard threshold compromise denoising method for weld forming measurement
-
摘要: 利用线激光视觉传感器对焊缝成形进行测量，焊缝图像往往存在噪声. 针对传统小波阈值去噪算法中硬阈值函数和软阈值函数的不足，研究焊缝图像软硬阈值折衷去噪算法. 利用db4小波基函数对激光条纹中心进行3层小波分解，对分解后的细节系数分别采用传统小波阈值函数和软硬阈值折衷法进行去噪，采用信噪比和均方根误差评价几种方法的去噪效果. 结果表明，软硬阈值折衷法的去噪效果优于传统小波阈值去噪法，能有效提高焊缝外形尺寸的测量精度及可靠性.Abstract: While a stripe laser vision sensor is used to measure the welded forming size, the noise is often existing in a weld image. Aiming at the deficiencies of hard threshold function and soft threshold function in traditional wavelet threshold denoising algorithm, a denoising algorithm based on Soft-hard Threshold Compromise method is studied. Using db4 wavelet basis function, three layers with wavelet decomposition of laser stripe center are performed. The traditional wavelet threshold function and Soft-hard Threshold Compromise method are applied to denoise the detail coefficients, and the denoising effects of several methods are evaluated by SNR and RMSE. Experimental results show that the Soft-hard Threshold Compromise method is better than the traditional wavelet threshold method for denoising, which can effectively improve the measurement accuracy and stability of weld forming size.
-
0. 序言
在现代工业中，焊接已经成为一种重要的加工技术，焊接质量检测是保证焊接质量的重要手段[1-3]. 对于焊后焊缝表面成形质量检测，传统检测法是通过人工目测观察和测量来实现，检测结果依赖检测者的主观判断，难以满足现代化生产需要[4].
与传统检测方法相比，直接视觉检测法是利用摄像机直接拍摄焊缝图像[5-6]，根据焊缝在图像中的灰度分布，利用图像处理方法获得焊缝表面形态信息. 但由于环境光照干扰，检测结果有时并不准确.
基于线激光视觉传感测量技术，利用三角测量原理，根据线激光条纹中的变形来获取焊缝形态信息[7-8]. 由于受环境光照、机械振动及传感器质量影响，焊缝激光条纹图像往往存在噪声，且主要集中在图像的高频部分. 常用的时域及频域去噪法通过保留焊缝图像低频分量与抑制高频分量来完成图像平滑，平滑后的图像减少了噪声干扰，但图像也会变模糊. 焊缝图像的高频分量不仅包含噪声，也包含焊缝轮廓的细节信息，通过抑制焊缝图像高频分量虽能达到降噪目的，但会丢失焊缝轮廓的一些细节信息，影响焊缝测量. 在此提出采用软硬阈值折衷法的小波阈值去噪法，在保留焊缝图像低频分量的同时，也对高频分量进行处理，消除噪声对焊缝成形测量的干扰，有效提高焊缝测量精度及可靠性.
1. 试验装置及测量原理
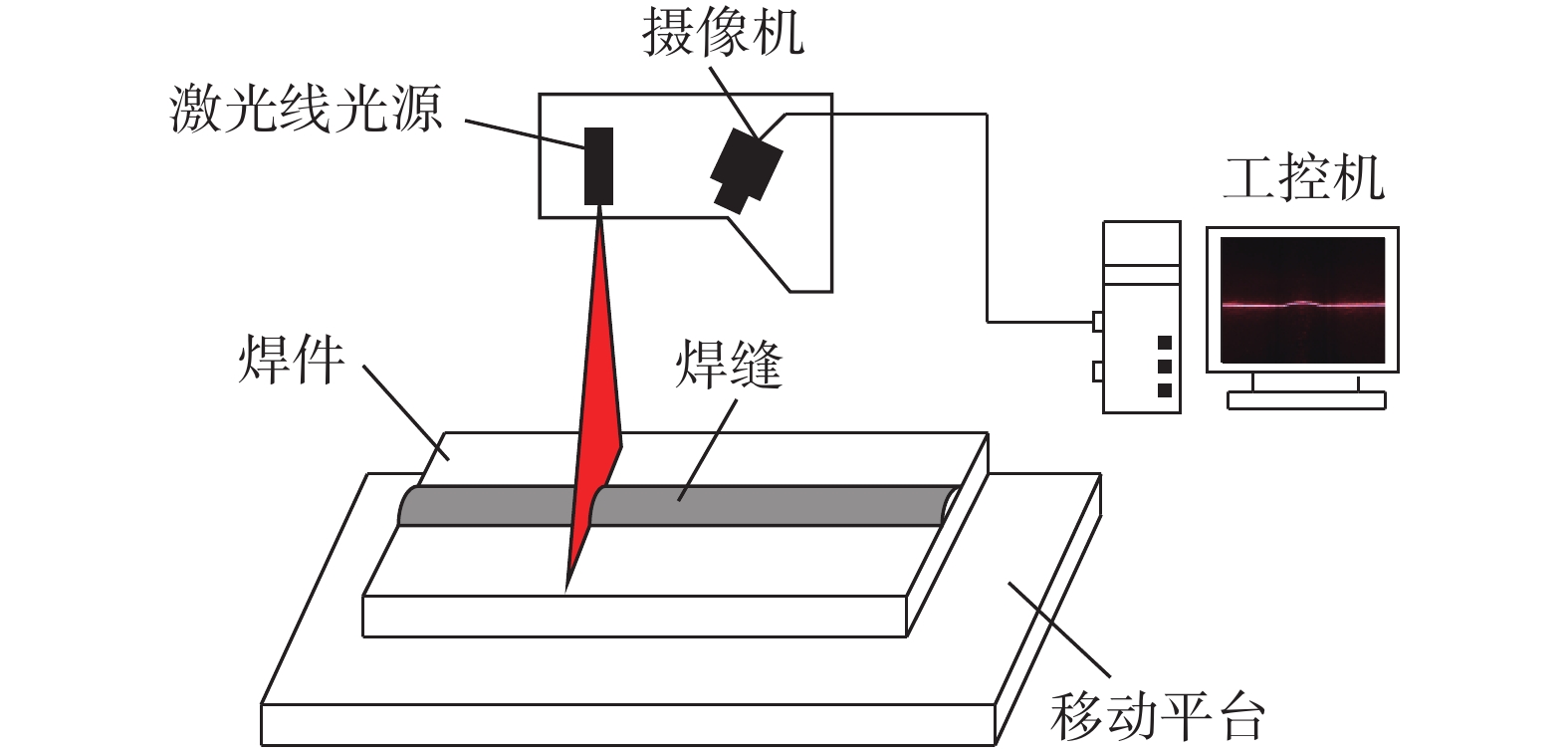
试验装置由摄像机、半导体线激光器、移动平台及工控机组成，如图1所示. 摄像机为300万像素工业相机，线激光器输出波长为650 nm. 摄像机和线激光器相对固定，根据三角测量原理，线激光器发出的光线垂直打在焊缝表面，利用摄像机对焊缝表面进行拍摄获取焊缝图像. 同时工作平台匀速移动，摄像机拍摄的图像通过数据线输入到工控机中，利用图像处理获取焊缝形态信息.
![]()
图 1 线激光焊缝成形测量试验装置原理图Figure 1. Testing schematic of weld forming measurement system based upon stripe laser2. 线激光焊缝成形测量系统标定
焊缝成形视觉测量需要建立被测焊缝的世界坐标系与其图像坐标系之间的转换关系，摄像机图像坐标系与世界坐标系的关系表示为[9]
$${{\textit{z}}_{\rm{c}}}\left[ {\begin{array}{*{20}{c}} u \\ v \\ 1 \end{array}} \right] = \omega \left[ {\begin{array}{*{20}{c}} {{x_{\rm{w}}}} \\ {{y_{\rm{w}}}} \\ {{{\textit{z}}_{\rm{w}}}} \\ 1 \end{array}} \right]$$ (1) $$\omega = \left[ {\begin{array}{*{20}{c}} {f/{d_x}}&0&{{u_0}}&0 \\ 0&{f/{d_y}}&{{v_0}}&0 \\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{R}}&{{T}} \\ {{{{0}}^T}}&{{1}} \end{array}} \right]$$ (2) 式中：(u, v)为焊缝特征点的图像坐标；(xw, yw, zw)为特征点对应的世界坐标；zc为摄像机坐标系下对应点的纵坐标；f表示相机焦距；dx，dy分别为像素点在成像平面坐标系中X轴和Y轴的物理尺寸；(u0, v0)为摄像机主点坐标；R为旋转矩阵；T为平移向量；ω为比例系数，可由式(2)计算获得.
在标定过程中，由于图像存在径向畸变，因此需对图像做畸变矫正，畸变矫正模型表达式为
$$\left[ {\begin{array}{*{20}{c}} {{x'}} \\ {{y'}} \end{array}} \right] = \left[ {k\left({x'^{2}} + {y'^{2}}\right) + 1} \right]\left[ {\begin{array}{*{20}{c}} x \\ y \end{array}} \right]$$ (3) 式中：(x, y)为畸变矫正前特征点图像坐标；(x′, y′)为矫正后特征点对应图像坐标；k为畸变系数.
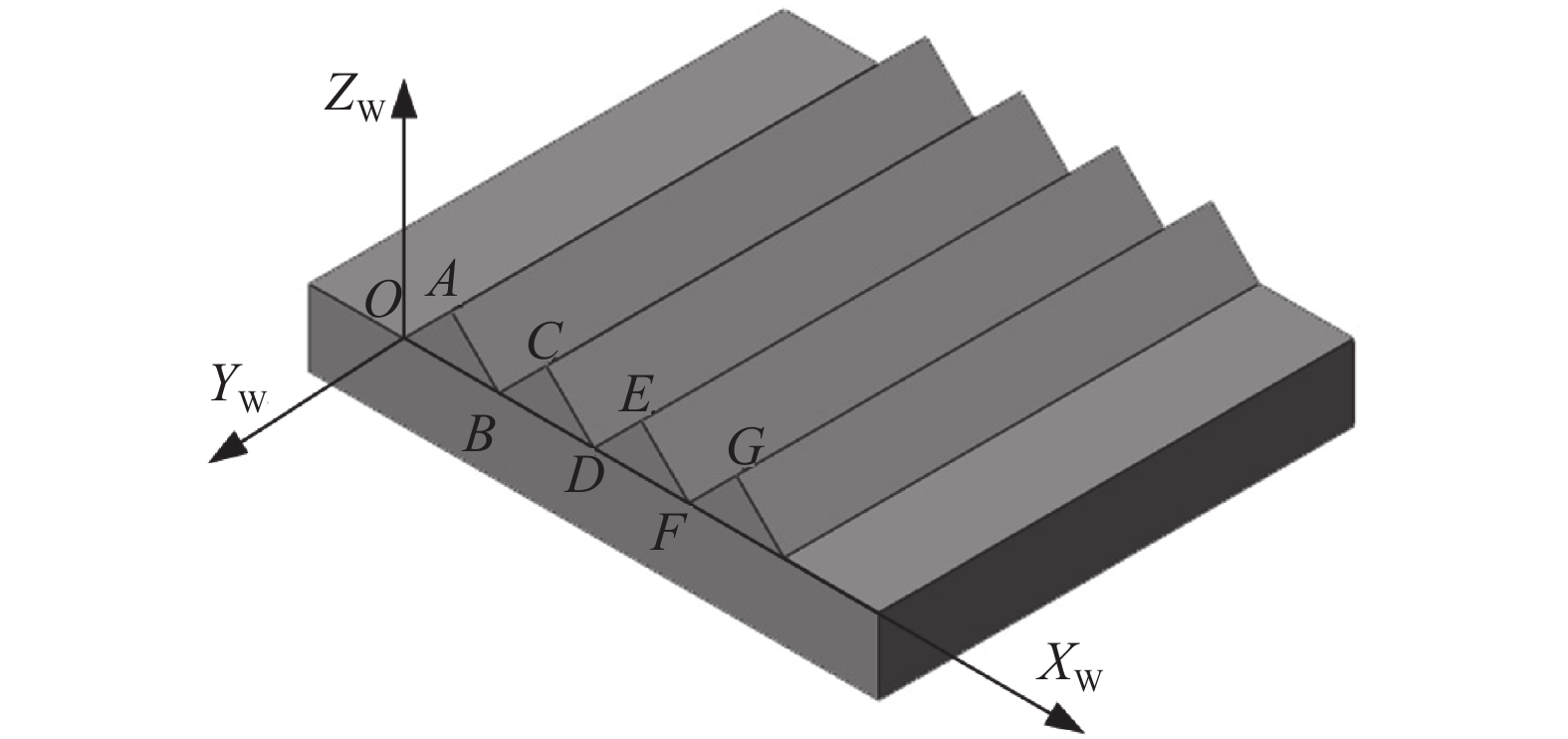
试验采用锯齿靶标标定法，锯齿间距为10 mm，齿高为5 mm，齿顶与齿根夹角为90 º，齿数为4，图2为锯齿靶标示意图. 标定时X轴和Y轴保持不动，不断调整Zw的高度，从而获得一系列特征点的图像坐标和世界坐标，根据式(1)得到标定矩阵，建立被测焊缝的世界坐标系与其图像坐标系之间的转换关系.为测试焊缝成形测量系统的标定精度，试验选用0级量块中的10，20与30 mm量块，在测量高度不变的情况下对每个量块重复摆放测量10次，测量结果如表1所示.
表 1 不同规格量块高度测量结果Table 1. Results of measurement in height with different gauge blocks量块标准值 h/mm 平均值 H/mm 标准偏差 δ/mm 误差 Δδ/mm 10 9.969 0.019 0.031 20 19.951 0.014 0.049 30 29.934 0.021 0.066 由表1分析可知，随着量块的测量值增加，测量误差也逐渐增大，原因是当量块测量值逐渐增加时，激光条纹在图像坐标系中逐渐上移而远离镜头中心，因此畸变也逐渐增大.
3. 小波阈值去噪
小波阈值去噪法是对含噪焊缝图像通过条纹中心提取方法获取焊缝条纹中心，利用小波多尺度分解获得焊缝条纹中心的各层细节分量，在各层细节分量中设定阈值，根据阈值对各层细节分量进行相应的保留或收缩，再利用小波逆变换最终重构出去噪后的焊缝条纹中心.
传统的小波阈值函数主要有硬阈值和软阈值，硬阈值函数表达式为[10-11]
$${\tilde w_{j,k}} = \left\{ {\begin{array}{*{20}{l}} {{w_{j,k}},}&{\left| {{w_{j,k}}} \right| \geqslant \lambda } \\ {0,}&{\left| {{w_{j,k}}} \right| < \lambda } \end{array}} \right.$$ (4) 软阈值函数表达式为
$${\tilde w_{j,k}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{sgn}}({w_{j,k}})\left(\left| {{w_{j,k}}} \right| - \lambda \right),}&{\left| {{w_{j,k}}} \right| \geqslant \lambda } \\ {0,}&{\left| {{w_{j,k}}} \right| < \lambda } \end{array}} \right.$$ (5) 式中：wj,k为小波系数；
${\tilde w_{j,k}}$ 为经阈值处理后的小波系数；λ为阈值，阈值的计算方法有全局阈值、启发式阈值和stein无偏似然估计等.硬阈值和软阈值去噪算法存在一些不足，硬阈值函数在λ处不连续，对于各层细节分量，经阈值处理后获得的小波系数会产生附加震荡；软阈值函数虽然连续，但当|wj,k|大于λ时，
${\tilde w_{j,k}}$ 与wj,k之间存在恒定偏差，影响焊缝条纹中心的真实性.为克服两种阈值函数的不足，提出采用软硬阈值折衷法对提取的焊缝条纹中心进行降噪处理，函数表达式为$${\tilde w_{j,k}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{sgn}}({w_{j,k}})\left(\left| {{w_{j,k}}} \right| - a\lambda \right),}&{\left| {{w_{j,k}}} \right| \geqslant \lambda } \\ {0,}&{\left| {{w_{j,k}}} \right| < \lambda } \end{array}} \right.$$ (6) 式中：a分别取0和1时，函数分别对应硬阈值函数和软阈值函数. 当0 < a < 1时，经阈值处理得到的小波系数介于硬阈值函数及软阈值函数之间. 经多次试验发现a = 0.1时去噪效果最佳.
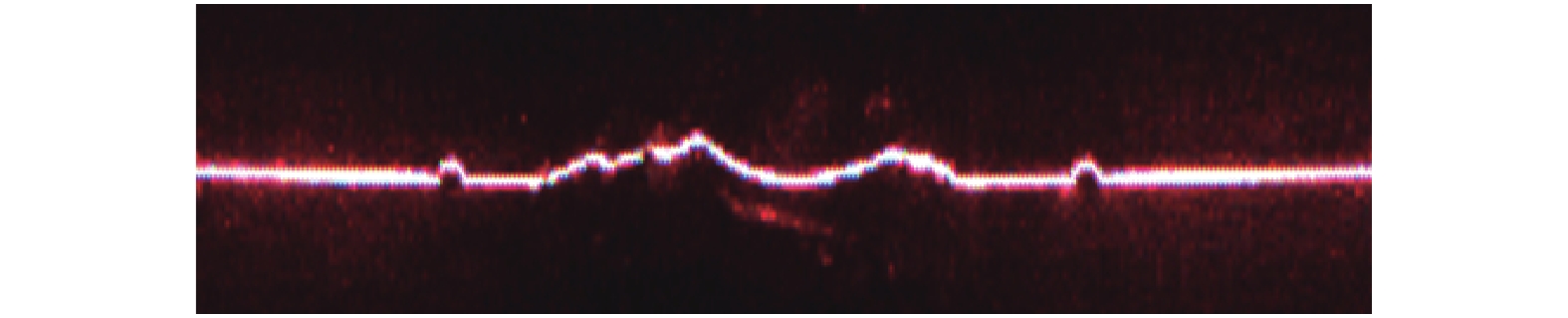
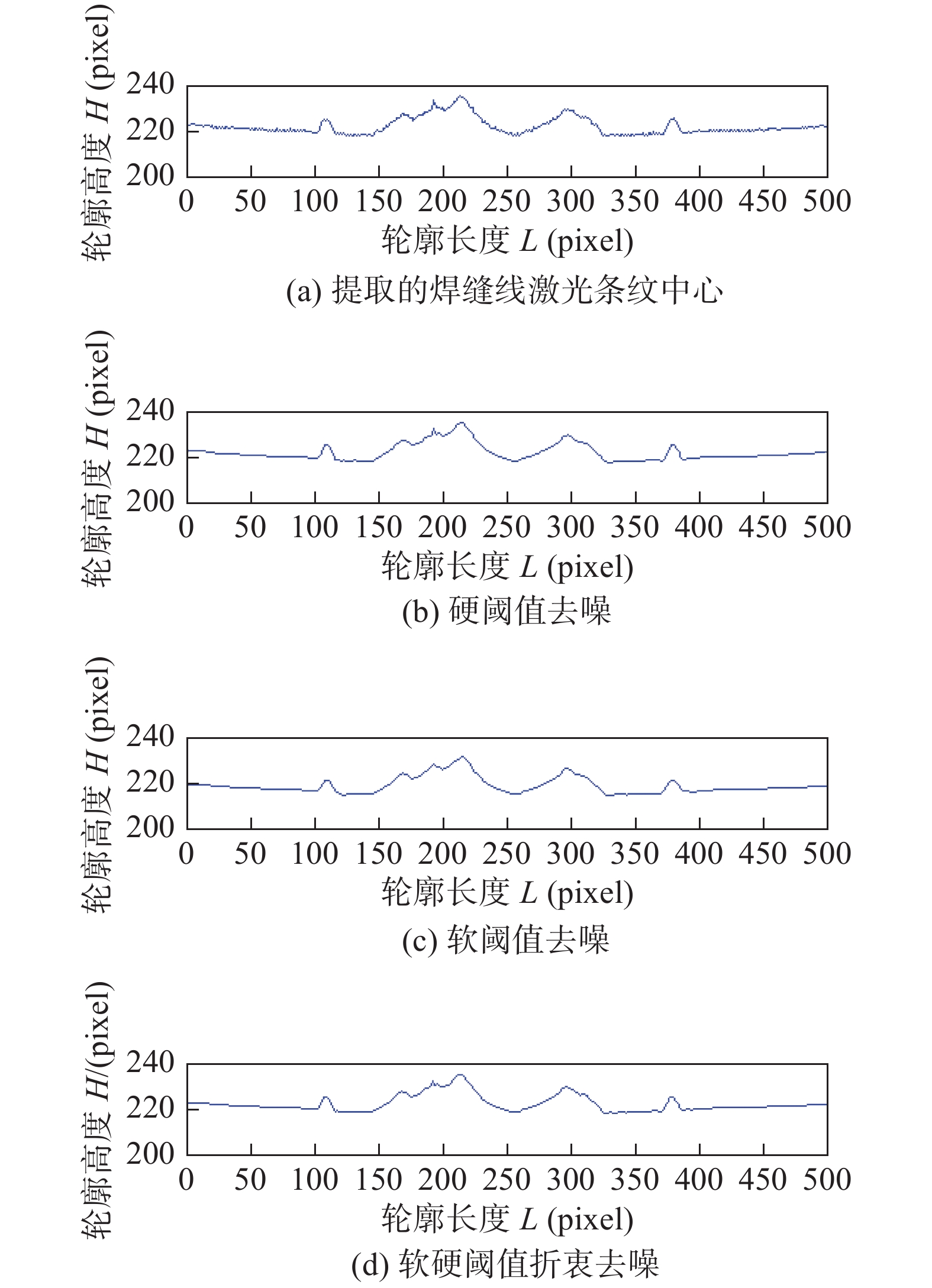
试验采用db4小波基函数对提取的焊缝条纹中心进行3层小波分解. 根据全局阈值，分别采用硬阈值法、软阈值法和软硬阈值折衷法对分解后获得的各层细节分量进行阈值降噪. 利用小波逆变换重构出降噪后的焊缝条纹中心. 图3为焊缝的线激光条纹图像，图4为3种阈值函数的去噪效果.
![]()
图 4 3种阈值函数去噪效果Figure 4. Denoising effect of three threshold functions. (a) extracted center of weld line laser stripe; (b) hard threshold denoising; (c) soft threshold denoising; (d) soft-hard threshold compromise denoising method焊缝条纹中心的去噪效果可以采用信噪比和均方根误差来衡量，设去噪前的信号为x(n)，去噪后的信号为x′(n)，信噪比表示为
$$SNR = 10 \cdot {\lg}\left( {\frac{{\displaystyle\sum\limits_{n = 1}^N {{x^2}(n)} }}{{\displaystyle\sum\limits_{n = 1}^N {{{\left[ {x(n) - {x'}(n)} \right]}^2}} }}} \right)$$ (7) 均方根误差表示为
$$RMSE = \sqrt {\frac{1}{n} \cdot {{\sum\limits_{n = 1}^N {\left[ {x(n) - {x'}(n)} \right]} }^2}} $$ (8) 表2为3种不同阈值函数处理后得到的信噪比和均方根误差.
表 2 3种处理方法的信噪比和均方根误差比较Table 2. Comparison of SNR and RMSE between three methods阈值函数 信噪比 SNR(dB) 均方根误差 RMSE (pixel) 硬阈值 55.876 9 0.357 4 软阈值 54.314 1 0.427 8 软硬阈值折衷 56.187 2 0.344 8 分析可知采用软硬阈值折衷法处理得到的信噪比最高，同时均方根误差最小. 对图5所示对接焊缝利用线激光进行扫描，扫描长度为150 mm，扫描速度为1 mm/s. 扫描后获得重构后的焊缝三维图像，根据对比发现经软硬阈值折衷法降噪处理后的焊缝图像保留了细节信息，且图像更加平滑.
![]()
图 5 焊缝三维重构图Figure 5. 3D reconstruction figure of weld seam. (a) butt weld; (b) fillet weld; (c) weld 3D diagram after denoising with median filter; (d) weld 3D diagram after soft-hard threshold compromise denoising method4. 试验结果与可靠性分析
为测试焊缝成形测量系统的可靠性，对图5中对接焊缝和角焊缝进行测量，分别采用软硬阈值折衷法和中值滤波对提取的焊缝激光条纹中心进行去噪处理，采用斜率截距法获得焊缝熔宽，连续测量10次取均值，表3为测量结果.
分析数据可知，在对接焊缝中同一焊缝位置，经软硬阈值折衷法去噪和中值滤波去噪测量的焊缝熔宽与实际值对比，最小偏差分别为0.01和0.02 mm，最大偏差分别为0.05和0.14 mm；在角焊缝中同一焊缝位置，经软硬阈值折衷法去噪和中值滤波去噪测量的焊缝熔宽与实际值对比，最小偏差为0.01 mm，最大偏差分别为0.04和0.11 mm. 经软硬阈值折衷法去噪后测量的焊缝熔宽波动范围比普通去噪法处理后的波动范围更小，说明采用软硬阈值折衷法的小波阈值去噪能够有效提高焊缝外形尺寸的测量精度及测量可靠性.
表 3 焊缝熔宽测量值对比(mm)Table 3. Comparison of measured weld seam width序号 对接焊缝 角焊缝 实际值 中值滤波 软硬阈值折衷法 实际值 中值滤波 软硬阈值折衷法 1 21.45 21.47 21.495 10.81 10.82 10.828 2 21.51 21.556 21.52 10.84 10.756 10.83 3 21.51 21.65 21.519 10.82 10.763 10.833 4 21.53 21.781 21.58 10.83 10.94 10.82 5 21.47 21.449 21.501 10.82 10.763 10.835 6 21.52 21.554 21.518 10.85 10.754 10.828 7 21.43 21.546 21.508 10.79 10.757 10.814 8 21.53 21.545 21.554 10.86 10.973 10.82 9 21.49 21.553 21.505 10.84 10.95 10.829 10 21.48 21.62 21.49 10.86 10.743 10.831 平均值 21.492 21.572 21.519 10.832 10.821 10.826 5. 结论
(1) 与传统的小波阈值去噪方法相比，软硬阈值折衷法的降噪效果与参数a有关，当0 < a < 1时，经阈值处理得到的小波系数介于硬阈值和软阈值之间，经多次试验发现a取0.1时去噪效果最佳.
(2) 针对传统小波阈值去噪算法对含噪焊缝图像去噪性能的不足，提出软硬阈值折衷去噪法. 试验表明采用软硬阈值折衷法的去噪性能优于传统小波阈值去噪方法，能有效提高焊缝外形尺寸的测量精度及可靠性.
-
![]()
图 1 线激光焊缝成形测量试验装置原理图
Figure 1. Testing schematic of weld forming measurement system based upon stripe laser
![]()
图 4 3种阈值函数去噪效果
Figure 4. Denoising effect of three threshold functions. (a) extracted center of weld line laser stripe; (b) hard threshold denoising; (c) soft threshold denoising; (d) soft-hard threshold compromise denoising method
![]()
图 5 焊缝三维重构图
Figure 5. 3D reconstruction figure of weld seam. (a) butt weld; (b) fillet weld; (c) weld 3D diagram after denoising with median filter; (d) weld 3D diagram after soft-hard threshold compromise denoising method
表 1 不同规格量块高度测量结果
Table 1 Results of measurement in height with different gauge blocks
量块标准值 h/mm 平均值 H/mm 标准偏差 δ/mm 误差 Δδ/mm 10 9.969 0.019 0.031 20 19.951 0.014 0.049 30 29.934 0.021 0.066 
下载: 导出CSV
表 2 3种处理方法的信噪比和均方根误差比较
Table 2 Comparison of SNR and RMSE between three methods
阈值函数 信噪比 SNR(dB) 均方根误差 RMSE (pixel) 硬阈值 55.876 9 0.357 4 软阈值 54.314 1 0.427 8 软硬阈值折衷 56.187 2 0.344 8
下载: 导出CSV
表 3 焊缝熔宽测量值对比(mm)
Table 3 Comparison of measured weld seam width
序号 对接焊缝 角焊缝 实际值 中值滤波 软硬阈值折衷法 实际值 中值滤波 软硬阈值折衷法 1 21.45 21.47 21.495 10.81 10.82 10.828 2 21.51 21.556 21.52 10.84 10.756 10.83 3 21.51 21.65 21.519 10.82 10.763 10.833 4 21.53 21.781 21.58 10.83 10.94 10.82 5 21.47 21.449 21.501 10.82 10.763 10.835 6 21.52 21.554 21.518 10.85 10.754 10.828 7 21.43 21.546 21.508 10.79 10.757 10.814 8 21.53 21.545 21.554 10.86 10.973 10.82 9 21.49 21.553 21.505 10.84 10.95 10.829 10 21.48 21.62 21.49 10.86 10.743 10.831 平均值 21.492 21.572 21.519 10.832 10.821 10.826
下载: 导出CSV
-
[1] Gao X D, Ma N J, Du L L. Magneto-optical imaging characteristics of weld defects under alternating magnetic field excitation[J]. Optics Express, 2018, 26(8): 9972. doi: 10.1364/OE.26.009972
[2] 迟大钊, 马子奇, 程怡, 等. 不等厚板搭接焊缝缺陷数字X射线检测[J]. 焊接学报, 2019, 40(11): 45 − 48. doi: 10.12073/j.hjxb.2019400286 Chi Dazhao, Ma Ziqi, Cheng Yi, et al. X-ray based defect testing method for a lap joint with unequal thickness steel plates[J]. Transactions of the China Welding Institution, 2019, 40(11): 45 − 48. doi: 10.12073/j.hjxb.2019400286
[3] Qi Jiyang, Li Jinyan. Feature extraction of welding defect based on machine vision[J]. China Welding, 2019, 28(1): 60 − 66.
[4] Rodríguez-Martín M, Lagüela S, González-Aguilera D, et al. Procedure for quality inspection of welds based on macro-photogrammetric three-dimensional reconstruction[J]. Optics & Laser Technology, 2015, 73: 54 − 62.
[5] Park J K, An W H, Kang D J. Convolutional neural network based surface inspection system for non-patterned welding defects[J]. International Journal of Precision Engineering and Manufacturing, 2019, 20(6): 363 − 374.
[6] Sun J, Li C, Wu X, et al. An effective method of weld defect detection and classification based on machine vision[J]. IEEE Transactions on Industrial Informatics, 2019, 15(12): 6322 − 6333. doi: 10.1109/TII.2019.2896357
[7] Wang N F, Zhong K, Shi X D, et al. A robust weld seam recognition method under heavy noise based on structured-light vision[J]. Robotics and Computer Integrated Manufacturing, 2020, 61(2): 101821.1 − 101821.9. doi: 10.1016/j.rcim.2019.101821
[8] 张斌, 常森, 王桔, 等. 基于遗传算法的激光视觉焊缝特征点提取[J]. 中国激光, 2019, 46(1): 80 − 90. Zhang Bin, Chang Sen, Wang Ju, et al. Feature points extraction of laser vision weld seam based on genetic algorithm[J]. Chinese Journal of Lasers, 2019, 46(1): 80 − 90.
[9] 张鹏贤, 李明, 代敦三. 基于激光扫描的焊缝成形尺寸测量[J]. 上海交通大学学报, 2014, 48(5): 636 − 640. Zhang Pengxian, Li Ming, Dai Dunsan. Measurement of welding formation size based on laser line scanning[J]. Journal of Shanghai Jiaotong University, 2014, 48(5): 636 − 640.
[10] 肖静, 游世辉. 基于小波变换的发动机表面缺陷图像去噪方法的研究[J]. 表面技术, 2018, 47(12): 328 − 333. Xiao Jing, You Shihui. Denoising method of engine surface defect image based on wavelet transform[J]. Surface Technology, 2018, 47(12): 328 − 333.
[11] 汪殿龙, 张志洋, 梁志敏, 等. 基于小波分析的交流CMT焊接电信号滤波[J]. 焊接学报, 2014, 35(5): 17 − 20. Wang Dianlong, Zhang Zhiyang, Liang Zhimin, et al. Electric signals filtering of AC CMT welding based on wavelet analysis[J]. Transactions of the China Welding Institution, 2014, 35(5): 17 − 20.
-
期刊类型引用(4)
1. 刘文吉，朱鹏飞，于镇洋，杨嘉昇，肖宇. 基于电流多特征融合的窄间隙P-GMAW摆动电弧传感焊缝跟踪方法. 传感技术学报. 2024(04): 612-619 . 
百度学术
2. 贾爱亭，洪波，李湘文，高佳篷，吴格飞，屈原缘. 基于轨迹在线识别的3D折线焊缝机器人摆动GMAW实时跟踪方法. 机械工程学报. 2022(14): 116-125 . 百度学术
3. 聂春萌，杨建伟. 虚拟现实系统中多自由度电磁跟踪方法仿真. 计算机仿真. 2019(04): 330-333 . 百度学术
4. 李高阳，洪宇翔，祝团结，刘锦. 一种摆动电弧CO_2焊焊缝表面状态自适应的新方法. 工程技术研究. 2019(16): 1-4 . 百度学术
其他类型引用(8)
计量
- 文章访问数: 387
- HTML全文浏览量: 53
- PDF下载量: 31
- 被引次数: 12
