Numerical simulation of double-sided explosive welding of stainless steel/ordinary carbon steel
-
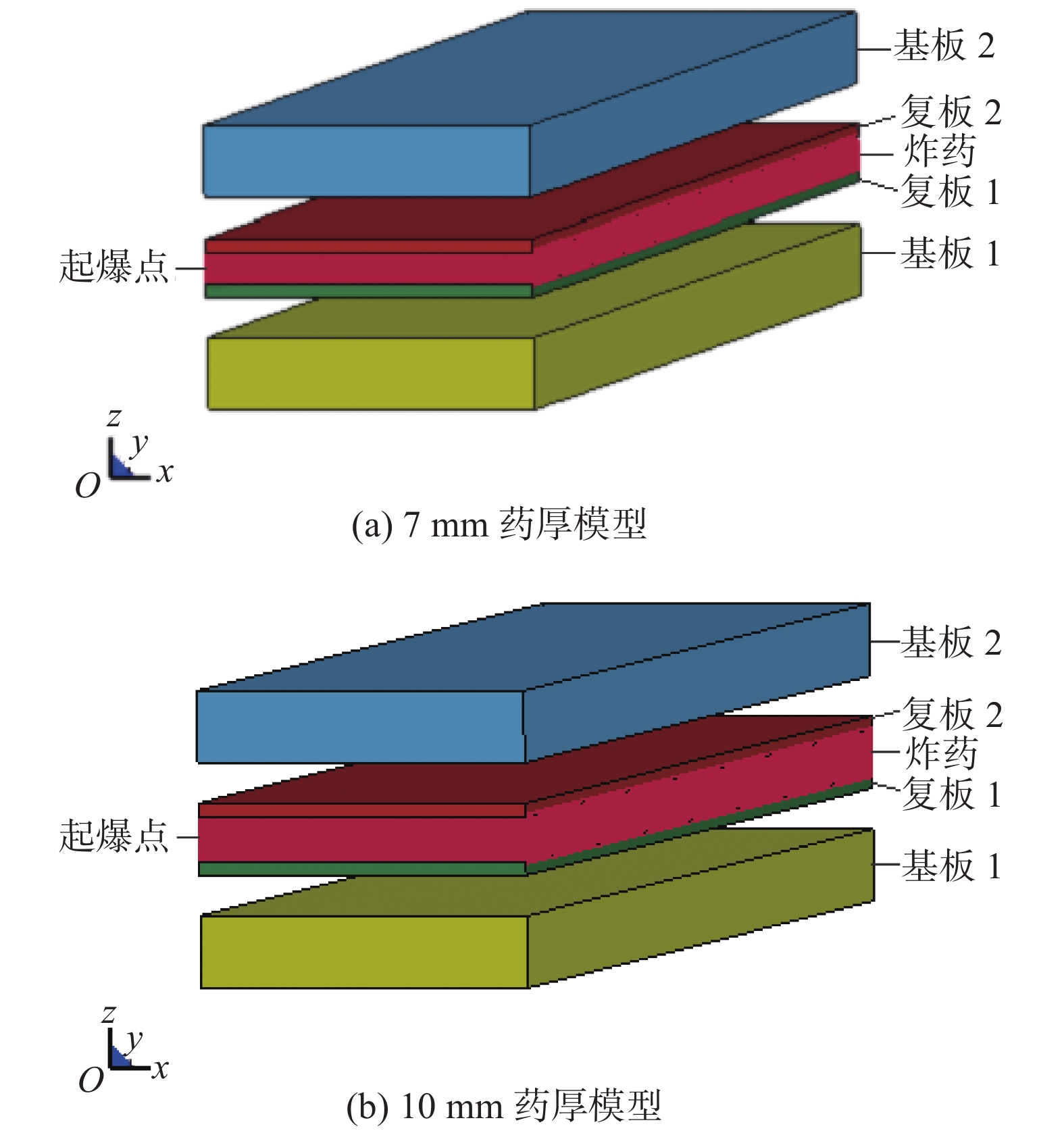
摘要: 为了提高能量的利用率，使用双面爆炸焊接装置可以一次性得到两块复合板. 借助LS-DYNA软件与光滑粒子流体动力学，采用SPH-FEM耦合算法，选取厚度为3 mm的304不锈钢、16 mm的Q235钢和乳化炸药，对不锈钢/普碳钢的双面爆炸焊接试验做了三维数值模拟，计算并建立了爆炸焊接窗口. 对模拟过程中的复板竖向位移、碰撞压力和碰撞速度进行了分析，并将模拟得到的结果与试验结果进行了比较. 模拟结果表明，7 mm药厚下复合质量较好，而10 mm药厚下可能会由于碰撞能量过大导致焊接失效，模拟与试验结果一致性较好. 引入了Gurney公式对试验结果进行预测，计算结果显示：Gurney公式的预测结果与试验结果吻合较好，表明了SPH-FEM耦合算法与Gurney公式用于不锈钢/普碳钢双面爆炸焊接的有效性.Abstract: In order to improve the utilization rate of energy, two composite plates can be obtained at one time by using a double-sided explosive welding device. With the help of LS-DYNA software and smoothed particle hydrodynamics, SPH-FEM coupling algorithm was adopted. Three-dimensional numerical simulations were made for the double-sided explosive welding experiment of stainless steel/ordinary carbon steel by selecting 304 stainless steel with the thickness of 3 mm, Q235 steel with 16 mm and emulsion explosives. The explosive welding window was calculated and established. The vertical displacement, collision pressure and collision velocity were analyzed, and the simulation results were consisted with the experimental results. The simulation results show that the composite quality is better under the thickness of 7 mm, while the welding failure may be caused by the excessive collision energy under the thickness of 10 mm. The simulation results were in accordance with the experimental results. The Gurney formula was introduced to predict the experimental results. The calculation results show that the prediction results of the Gurney formula are in good agreement with the experimental results, indicating that the SPH-FEM coupling algorithm and Gurney formula are effective for double-sided explosive welding of stainless steel/ordinary carbon steel.
-
Keywords:
- double-sided explosive welding /
- 304 steel /
- Q235 steel /
- numerical simulation
-
0. 序言
搅拌摩擦焊是一种固相焊接工艺，焊接过程中搅拌头在待焊工件中旋转，并沿焊接方向移动.在物理摩擦和材料塑性变形的共同作用下，搅拌头使得搅拌头附近的材料热塑化，并将焊接区的材料混合，最终形成致密的固相连接[1].相对于传统熔化焊接头，搅拌摩擦焊接头具有组织致密、热变形小等特点[2].随着基础研究的不断深入，国内外研究机构和企业已将搅拌摩擦焊技术应用到了航空航天工业[3]、船舶制造工业[4-5]、汽车零部件制造[6]、轨道交通移动装备[7-9]等诸多领域.
在传统的单轴肩搅拌摩擦焊过程中，下压量是保证焊接质量关键参数[4].因此，在焊接位置的背面提供有效的刚性支撑是实现良好焊接的必要先决条件.然而，对于具有封闭、中空等复杂结构的工件，当无法提供背部刚性支撑时，单轴肩搅拌摩擦焊便无法实施.虽然在部分情况中，可以通过接头结构的设计为单轴肩搅拌摩擦焊位置提供所需的背部支撑结构，但势必会增加工件的整体重量，影响产品整体的轻量化效果.新型双轴肩搅拌摩擦焊，在焊接工具结构中增设下轴肩，取代了单轴肩搅拌摩擦焊所需的背部刚性支撑，在无需轴向压紧力的条件下，即可实现中空复杂结构的搅拌摩擦焊[10].因此，在复杂结构工件，特别是中空型材的搅拌摩擦焊中，双轴肩搅拌摩擦焊具有广阔的应用前景.
双轴肩搅拌摩擦焊的焊接工具由上轴肩、搅拌针、下轴肩3个主要部分构成，搅拌针与下轴肩一般一体成型，并通过螺纹与上轴肩连接成为一个整体.上轴肩、搅拌针、下轴肩分别与材料摩擦产生热量，为双轴肩搅拌摩擦焊的主要热输入[11-12].针对轨道交通领域中常用的6061-T6铝合金中空薄壁型材进行双轴肩搅拌摩擦焊试验，基于热输入理论分析，建立焊接工具结构尺寸特征值与板厚关系的工程模型，指导设计焊接工具结构，优化结构尺寸.通过优化焊接工艺参数(如搅拌头转速、焊接速度等)，获得抗拉强度和弯曲性能优异的6061-T6铝合金中空薄壁型材对接接头.
1. 试验方法
试验采用FSW-HD型重载搅拌摩擦焊设备. 图1为焊接设备及工装. 在双轴肩搅拌摩擦焊过程中，需要通过垫板、挡板、定位块、压板等组成的工装(图1b)对待焊型材进行装夹和固定，防止在焊接过程中待焊型材分离，保证焊接质量.
![]()
图 1 焊接设备及工装Figure 1. Welding equipment and fixture. (a) FSW-HD type friction stir welding equipment; (b) welding fixture实施双轴肩搅拌摩擦焊前，首先将型材焊接端面铣平，保证对接装配后待焊型材之间无间隙；然后将待焊型材清洗干净，安装在工装中；最后沿焊接方向调节装配的平行度及高度，为双轴肩搅拌摩擦焊做好准备. 在焊接过程中，根据搅拌头转速变化特点，可将焊接过程分为起始加速、匀速焊接、结尾退出3个阶段. 焊接完成后，获得成形良好的对接焊缝，并沿焊缝方向截取标准拉伸试样、弯曲试样，通过力学性能测试分析并评价焊缝性能.
按照GB/T 2651—2008《焊接接头拉伸试验方法》标准在EMSYS电子万能材料试验机上进行拉伸试验；按照GB/T 2653—2008《焊接接头弯曲试验方法》标准在Z1000电子万能材料试验机上进行弯曲试验.
6061-T6是Al-Mg-Si系铝合金，具有较好的可加工性、耐腐蚀性能和焊接性等特点，常通过挤压成型的方式制成具有一定功能特性截面结构的型材. 采用轨道交通产品中常用的6061-T6铝合金中空薄壁型材作为双轴肩搅拌摩擦焊工艺研究的材料.该型材由安徽鑫铂铝业股份有限公司加工制造. 型材结构如图2所示，多个型材对接，可以形成具有空腔的大型部件(图2b)，该部件为轨道交通产品的关键部件.对接位置板厚为2.5 mm.
![]()
图 2 型材结构Figure 2. Extruded profile structure. (a) cross section schematic of extruded profile; (b) large area structure formed by multiple components通过化学成分分析，验证型材成分满足GB/T 3190—2008 《变形铝及铝合金化学成分》中规定的6061铝合金化学成分要求，具体结果如表1所示.
表 1 6061铝合金中空薄壁型材化学成分(质量分数，%)Table 1. Chemical compositions of 6061-T6 aluminum alloy extruded profile项目 Mg Si Cu Cr Fe Zn Mn Al 实测值 0.851 0.688 0.161 0.086 0.143 0.016 0.081 余量 标准值 0.8 ~ 1.2 0.4 ~ 0.8 0.15 ~ 0.4 0.04 ~ 0.35 0 ~ 0.7 0 ~ 0.25 0 ~ 0.15 余量 通过力学性能测试获得母材的显微硬度为111 HV0.2，抗拉强度为298 MPa，屈服强度为276 MPa，断后伸长率为7.0%.具体测试结果如表2所示.
表 2 6061铝合金中空薄壁型材的力学性能Table 2. Mechanical properties of 6061-T6 aluminum alloy extruded profile编号 抗拉强度
Rm/MPa屈服强度
ReL/MPa断后伸长率
A(%)显微硬度
H(HV0.2)母材1 297 273 8.02 110 母材2 298 276 6.75 113 母材3 300 279 6.45 111 平均 298 276 7.07 111 2. 试验结果与分析
2.1 理论分析
根据搅拌摩擦焊焊接过程的产热特点，焊接工具的结构参数显著影响焊接过程的热输入，进而影响焊缝的成形质量[13].双轴肩搅拌摩擦焊工具的上、下轴肩间距与板厚存在一定的对应关系，且上轴肩直径、下轴肩直径、搅拌针直径等诸多结构参数均会对焊接质量产生影响. 针对特定厚度的待焊工件，如何能够快速和高效地选定焊接工具的主要结构参数、减少工具设计的迭代次数、降低开发成本是双轴肩搅拌摩擦焊工艺研发过程中必要且关键的问题. 通过对搅拌摩擦焊热输入的理论分析，推导并建立工具结构特征值与待焊工件厚度之间的经验方程，进而指导6061-T6铝合金双轴肩搅拌摩擦焊的工具选型，有效地解决了上述问题.
搅拌摩擦焊技术发展至今，其热源模型已有较多的研究[14-17]. 虽然不同学者对于模型的简化和等效方向不同，得出的热源解析模型也有一定的区别，但学界得到的一点共识是，搅拌摩擦焊过程中总的热输入Qtotal等于焊接工具与材料的摩擦产热Qf与材料塑性变形产热Qt之和[18]，如式(1)所示，且摩擦产热占总热输入的80%以上[16].
$$ Q_{{\rm{total}}} = Q_{{\rm{f}}} + Q_{{\rm{t}}} $$ (1) 塑性变形产热Qt由材料本身物化性质决定，而摩擦产热Qf与工具的结构参数密切相关.因此，进一步解析摩擦产热Qf的表达，为寻求摩擦产热Qf与工具结构参数之间的关系打下基础. 焊接工具与工件之间摩擦产热主要包括上轴肩与工件的摩擦产热、搅拌针与工件的摩擦产热以及下轴肩与工件之间的摩擦产热[16]，即
$$ Q_{{\rm{f}}} = Q_{{\rm{u}}} + Q_{{\rm{p}}} + Q_{{\rm{d}}} $$ (2) 式中：Qu为上轴肩与工件的摩擦产热；Qp为搅拌针与工件的摩擦产热；Qd为下轴肩与工件的摩擦产热.
为了简化分析，假设与工件接触的轴肩为无附加结构的水平面，搅拌针为无附加结构的规则圆柱体，轴肩与搅拌针之间直接过渡，无圆角、倒角等结构.
在上轴肩与工件摩擦的圆环面上，设搅拌针半径为Rp，上轴肩直径为Ru，可以得到图3中黑色微单元上摩擦产热功率dq为[19]，
![]()
图 3 轴肩与工件摩擦的圆环面示意图Figure 3. Schematic diagram of the ring area of friction between shoulder and workpiece$$ d_{{\rm{q}}}=w r \tau \cdot r {\rm{d}} \theta {\rm{d}} r=\tau a^{2} {\rm{d}} \theta {\rm{d}} r $$ (3) 式中：r为微单元到中心的距离；ω为焊接工具转速；τ为单位面积所受的摩擦力[20].将式(3)在圆环上积分，可以得到Qu，即
$$ {Q}_{\rm {u }}=\int_{R_{{\rm{p}}}}^{R_{\rm {u }}} \tau \omega r^{2} {\rm{d}} r \int_{0}^{2 {\text{π}}} {\rm{d}} \theta=\frac{2}{3} {\text{π}} \tau \omega\left(R_{\rm {u }}^{3}-R_{{\rm{p}}}^{3}\right) $$ (4) 设搅拌针高度为H，可以得到Qn，即
$$ {Q}_{\rm {p }}=\int_{0}^{H} \tau \omega R_{{\rm{p}}}^{2} {\rm{d}} l \int_{0}^{2 {\text{π}}} {\rm{d}} \theta=2 {\text{π}} \tau \omega R_{{\rm{p}}}^{2} H $$ (5) $$ {Q}_{\rm {d }}=\int_{R_{{\rm{p}}}}^{R_{{\rm{d}}}} \tau \omega r^{2} {\rm{d}} r \int_{0}^{2 {\text{π}}} {\rm{d}} \theta=\frac{2}{3} {\text{π}} \tau \omega\left(R_{\rm {d }}^{3}-R_{{\rm{p}}}^{3}\right) $$ (6) 联立式(2)、式(4)、式(5)和式(6)，得到焊接工具与工件之间摩擦产热Qf .
$$ {Q}_{\mathrm{f}}={Q}_{\rm {u }} + {Q}_{\rm {p }} + {Q}_{\rm {d }}=\frac{2}{3} {\text{π}} \tau \omega\left[R_{\rm {u }}^{3} + R_{\rm {d }}^{3}-R_{{\rm{p}}}^{2}\left(2 R_{{\rm{p}}}-3 H\right)\right] $$ (7) 由式(7)可见，决定焊接过程中热输入的参数时，除材料本身特性参数和焊接工艺参数外，焊接工具的结构参数也起到重要作用.该结构参数包含了上轴肩直径Ru、下轴肩直径Rd、搅拌针直径Rp、轴肩间距H等焊接工具的关键结构尺寸.将其定义为焊接工具的结构特征值S，即
$$ S=R_{\rm {u }}^{3} + R_{\rm {d }}^{3}-R_{{\rm{p}}}^{2}\left(2 R_{{\rm{p}}}-3 H\right) $$ (8) 在此基础上，通过调研针对某一种特定待焊材料的双轴肩搅拌摩擦焊的研究成果，可以获得焊接工具结构特征值S与待焊工件厚度d之间的关系，从而建立工程模型，指导焊接工具选型.
针对6061-T6的双轴肩搅拌摩擦焊，综合分析了国内外已报道的研究结果，获得焊接不同厚度d的工件使用的双轴肩搅拌摩擦焊工具的结构特征值S，详细数据如表3所示.
表 3 部分6061-T6铝合金双轴肩搅拌摩擦焊研究结果Table 3. Reported results of 6061-T6 aluminum alloy bobbing tool FSW文献
编号待焊材料厚度
d/mm上轴肩直径
Ru/mm下轴肩直径
Rd/mm轴肩间距
H/mm搅拌针直径
Rp/mm抗拉强度
Rm/MPa接头系数
η(%)特征值
S[21] 4 18 16 3.8 8 230 72 1 295.4 [22] 5 18 16 4.9 8 221 77 1 348.2 [23] 6 16 16 5.8 8 203 59 1 174.4 [24] 7.8 23 23 7.65 10 191 74 3 365.5 [25] 4 18 16 3.94 8 188 66 1 302.1 [26] 4 18 16 3.9 8 195 69 1 300.2 [27] 4 18 18 4 8 182 66 1 522 [28] 5 18 16 4.95 8 224 75 1 350.6 [29] 6.35 22 22 6 8 229 93 2 822 [30] 8 24 24 7.7 11.9 237 82 3 852.5 以待焊工件厚度d为自变量，结构特征值S为因变量，通过线性拟合的方法，可以获得S-d的拟合方程.由表3可以看出，对于文献[23]的研究结果，其焊接接头的抗拉强度仅达到母材强度的59%，未达到其它研究成果的平均水平(65%以上)，说明该研究中，双轴肩搅拌摩擦焊的焊接工具及工艺还有优化的空间.当不考虑文献[23]的数据时，如图4所示，S-d关系线性拟合的拟合度r0可达0.965.在特征值S与工件厚度d之间的关系表达为
$$ S = 508.6d - 703.1 $$ (9) 2.2 焊接工具优化
根据3.1节建立的焊接工具结构特征值S与待焊工件厚度d的关系的工程模型，当待焊工件厚度为2.5 mm时，焊接工具尺寸特征值S计算值为568.4. 基于特征值S对焊接工具结构进行设计，考虑理论模型与实际试验情况之间的偏差，认为设计的焊接工具结构特征值S在图4所示虚线区域内即为满足要求.共设计3种不同结构尺寸的焊接工具，焊接工具具体结构参数如表4所示. 焊接工具3的搅拌针为圆锥体，靠上轴肩侧锥台直径为6 mm，靠下轴肩侧锥台直径为4.5 mm.
表 4 FSW工具结构的尺寸参数Table 4. Dimension parameter of the FSW tool工具编号 上轴肩直径 Ru/mm 下轴肩直径 Rd/mm 轴肩间距 H/mm 搅拌针直径 Rp/mm 特征值S 1 16 16 2.3 6 1 032 2 12 12 2.3 6 440 3 14 12 2.3 6，4.5 552 当使用1号工具时，焊缝无法成形，且热塑化的材料易于粘黏在焊接工具的两个轴肩之间，如图5所示.焊接工具旋转经过待焊位置时，热塑化的材料沿焊接工具旋转线速度方向拉长，但无法完全填充搅拌针后留下的空隙，形成一个尺寸小于搅拌针直径的间隙.而且，焊接工具移动过程中，热塑化的材料受到轴肩施加的轴向挤压力，挤出焊接工具摩擦范围，生成连续飞边.通过试验现象分析后得知，焊接工具的上、下轴肩直径过大，导致因轴肩与工件摩擦产生的热输入过大，材料软化严重、流动性过强. 不仅使热塑化的材料易于被挤出焊接区域，还使得过于软化的材料在表面张力的作用下更倾向于粘附在上、下轴肩之间的间隙中，从而导致热塑化材料无法填充搅拌针移动方向后方的空隙，焊缝无法成形.
当使用2号工具时，焊缝虽在部分区域可以融合，但整体出现连续沟槽缺陷.即使通过调整焊接工艺参数，沟槽缺陷仍难以避免，如图6所示. 通过试验现象分析，认为焊接工具的上、下轴肩直径偏小，轴肩产生的热输入不足，使得材料不能充分软化，流动性不佳，从而导致材料无法充分流动并填充搅拌针后方的空隙，导致产生连续沟槽缺陷.
当使用3号工具时，可以有效实现工件的焊接，焊缝成形良好、美观.通过对比分析可以发现，当上、下轴肩直径适中时，焊接热输入适当，良好的材料流动使得搅拌针后方的空隙得到良好的填充，从而可以实现成功的焊接，如图7所示.
考虑使用 2.1 节中的工程模型式(8)计算得到的焊接工具结构特征值对焊接工具设计的指导意义. 1号工具的特征值S1为1 032，大于计算值，因此在焊接试验过程中容易引起过大的焊接热输入；2号工具的特征值S2为440，小于计算值，容易导致焊接热输入不足；3号工具的特征值S3为552，与计算值的差值较小，此时焊接热输入适当，可以实现焊接. 因此，当工具特征值与模型计算值之间偏差较小时，通过焊接工艺的调整实现焊缝的成形情况；但当工具特征值与模型计算值之间偏差较大时，焊接工艺的调整无法弥补因工具尺寸不合适导致的焊缝成形问题.
2.3 焊接工艺优化
使用3号工具进行试验，研究焊接工艺参数对接头力学性能的影响.以接头的抗拉强度与弯曲角度作为力学性能指标评价焊接工艺参数.为实现型材的对接焊，需在正、反两面分别施加双轴肩搅拌摩擦焊，并对正、反两面焊接接头力学性能进行综合评价.
图8为焊接速度为600 mm/min的条件下，不同搅拌头转速对焊接接头力学性能的影响.由图8可知，当搅拌头转速为1 000 r/min时，正、反两面焊接接头的抗拉强度均达到最大值，分别为231，226 MPa，且正、反两面焊接接头的弯曲角度均达到180°. 因此，该工艺参数焊接得到的焊接接头综合力学性能最佳.
![]()
图 8 不同转速下焊接接头的力学性能Figure 8. Mechanical properties of FSW joints with different rotation speeds为了满足工业应用及生产的需要，便于焊接工艺的实施，应扩大工艺参数窗口. 当搅拌头转速为1500 r/min时，正、反两面焊接接头也可以得到较高的抗拉强度，分别为210，179 MPa，且正、反两面焊接接头的弯曲角度也均达到180°. 因此，在搅拌头转速分别为1 000，1 500 r/min的条件下，继续对焊接速度进行优化，如图9所示. 从图9a可以看出，在搅拌头转速为1000 r/min时，仅当焊接速度为600 mm/min的工艺条件下，正、反两面焊接接头的弯曲角度可以达到180°，且抗拉强度较高，为231，226 MPa. 而在搅拌头转速为1500 r/min时，焊接速度为450，600，750 mm/min的工艺条件均能获得抗拉强度较高且弯曲角度达到180°的焊接接头，如图9b所示.
![]()
图 9 不同焊接速度下焊接接头的力学性能Figure 9. Mechanical properties of FSW joints with different weld speeds. (a) rotation speed of 1 000 r/min; (b) rotation speed of 1 500 r/min通过焊接工艺的优化，获得了4个较优的焊接工艺参数，可以获得综合力学性能良好的焊接接头，分别为搅拌头转速1 000 r/min、焊接速度600 mm/min，搅拌头转速1500 r/min、焊接速度450 mm/min，搅拌头转速1500 r/min、焊接速度600 mm/min，搅拌头转速1500 r/min、焊接速度750 mm/min. 其中，搅拌头转速1000 r/min、焊接速度600 mm/min工艺下获得的焊接接头综合力学性能最佳.
3. 结论
(1) 通过双轴肩搅拌摩擦焊热输入理论分析，推导出焊接工具结构参数特征值S. 根据国内外公布的6061-T6双轴肩搅拌摩擦焊的研究成果，建立工程模型表征特征值S与板厚d之间的关系为S = 508.6d - 703.1.
(2) 利用工程模型计算适用于焊接2.5 mm铝合金6061-T6的焊接工具特征值，并根据计算特征值设计3种焊接工具. 其中，3号工具上、下轴肩直径分别为14，12 mm，其结构特征值与工程模型计算值之间的差值最小. 从试验结果发现，3号工具的轴肩与待焊板材之间接触面积适当，热输入合适，材料流动使得材料可以流动并填充搅拌针后方的空隙，焊缝成形良好.
(3) 通过焊接工艺优化，获得4个较优的焊接工艺参数，可以获得综合力学性能良好的焊接接头. 其中，搅拌头转速1 000 r/min、焊接速度600 mm/min工艺下获得的焊接接头综合力学性能最佳，正面焊缝焊接接头抗拉强度可达231 MPa，为母材抗拉强度的77%，弯曲角度达180°；反面焊缝焊接接头抗拉强度可达226 MPa，为母材抗拉强度的76%，弯曲角度达180°.
-
![]()
图 1 计算模型
Figure 1. Calculation model. (a) 7 mm charge thickness; (b) 10 mm charge thickness
![]()
图 2 爆炸焊接竖向位移云图
Figure 2. Vertical displacement cloud map of explosion welding. (a) 17.988 μs; (b) 42.974 μs; (c) 70.984 μs
![]()
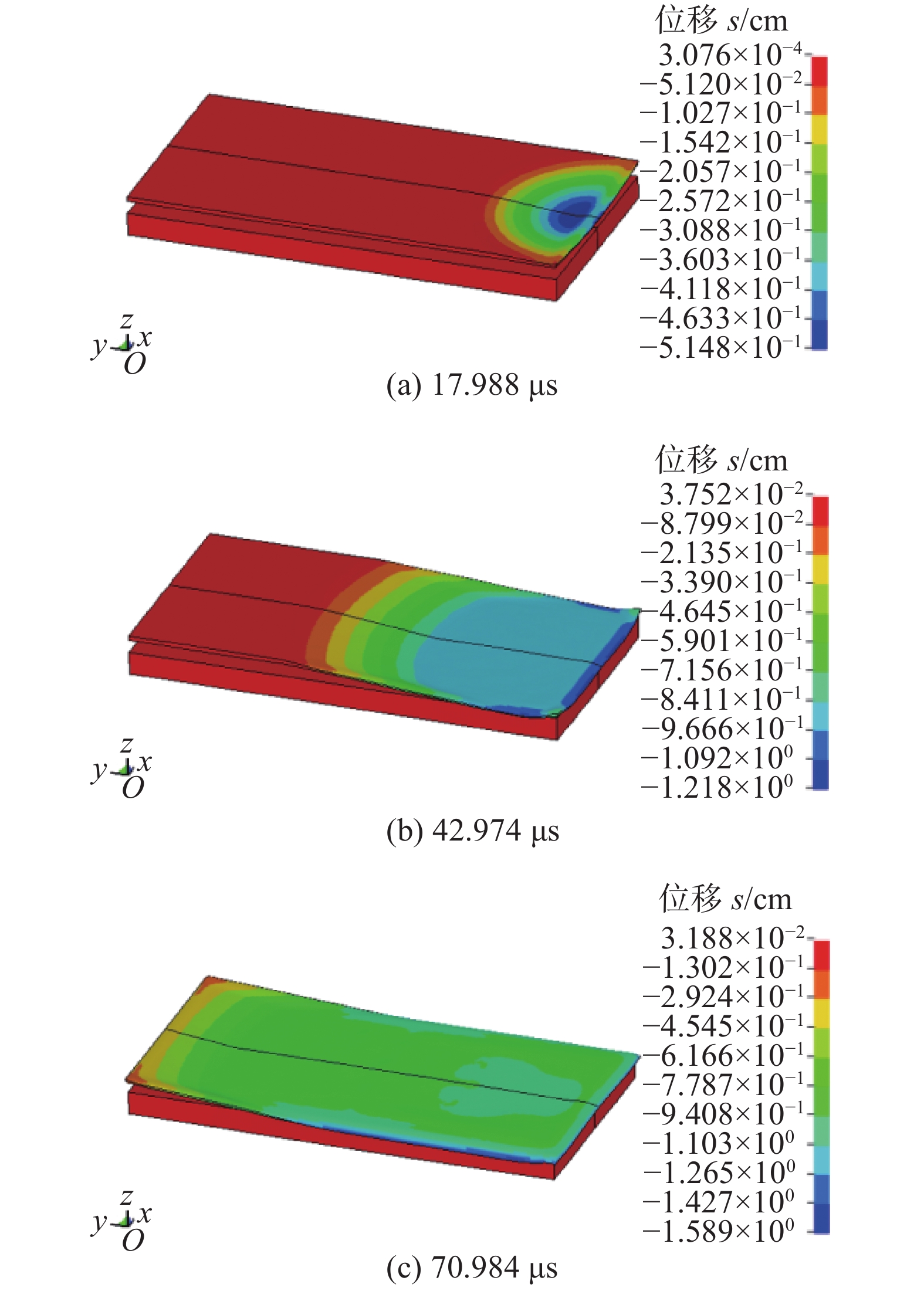
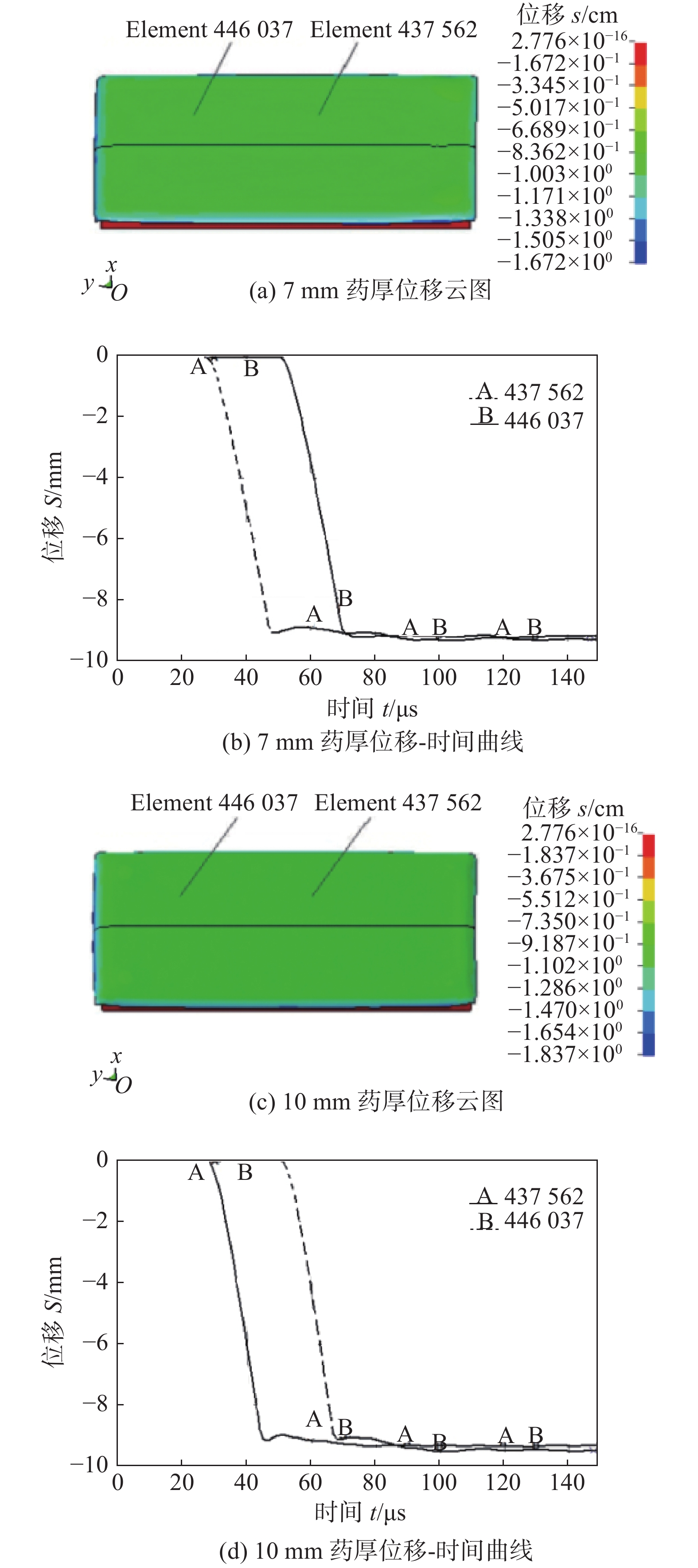
图 3 不同药厚下的竖向位移云图和位移-时间曲线
Figure 3. Vertical displacement cloud diagram and displacement-time curve under different charge thickness. (a) cloud diagram of 7 mm charge thickness; (b) displacement-time curve of 7 mm charge thickness; (c) cloud diagram of 10 mm charge thickness; (d) displacement-time curve of 10 mm charge thickness
![]()
图 4 压力分布图
Figure 4. Pressure distribution diagram. (a) t = 50.98 μs; (b) enlarged drawing of the collision point area
![]()
图 5 结合面上四对特征单元及压力-时间曲线
Figure 5. Four pairs of characteristic elements and pressure-time curve on the joint surface. (a) characteristic elements; (b) pressure-time curve
![]()
图 6 有效塑性应变分布图
Figure 6. Effective plastic strain distribution map. (a) t = 53.97 μs; (b) enlarged drawing of the joint surface
![]()
图 7 剪切应力分布图
Figure 7. Shear stress distribution map. (a) t = 53.97 μs; (b) enlarged drawing of the collision point area
![]()
图 8 复板上6个特征单元及速度-时间曲线
Figure 8. Six characteristic elements and velocity-time curve on flyer plate. (a) characteristic elements; (b) velocity-time curve
![]()
图 9 不同药厚下结合面一对特征单元及速度-时间曲线
Figure 9. A pair of characteristic elements and velocity-time curve of the joint surface under different drug thickness. (a) characteristic elements of 7 mm; (b) velocity-time curve of 7 mm; (c) characteristic elements of 10 mm; (d) velocity-time curve of 10 mm
![]()
图 10 7 mm药厚下爆炸复合板界面波形
Figure 10. Interface waveform of explosive composite plate with thickness of 7 mm; (a) interface waveform; (b) single waveform
表 1 乳化炸药的JWL状态参数
Table 1 JWL state parameters of emulsion explosive
AJWL/GPa BJWL/GPa R1 R2 ω E0/(kJ·cm−3) 326.42 5.808 9 5.80 1.56 0.57 3.323 
下载: 导出CSV
表 2 304不锈钢和Q235钢的Johnson-Cook模型参数
Table 2 Johnson-Cook model parameters of 304 steel and Q235 steel
参数 ρ/(g·cm−3) G/GPa A B n C m Tm/K Tr/K 304不锈钢 7.9 24 0.700 1.30 0.75 0.021 0.90 1 710 294 Q235钢 7.8 77 0.792 0.51 0.26 0.014 1.03 1 809 294
下载: 导出CSV
表 3 304不锈钢和Q235钢的Gruneisen方程参数
Table 3 Gruneisen equation parameters of 304 steel and Q235 steel
材料 c S1 $ \gamma $ A 304不锈钢 0.458 0 1.49 1.93 0.50 Q235钢 0.456 9 1.49 2.17 0.46
下载: 导出CSV
表 4 304不锈钢/Q235钢材料主要性能参数
Table 4 Main performance parameters of 304 steel/Q235 steel
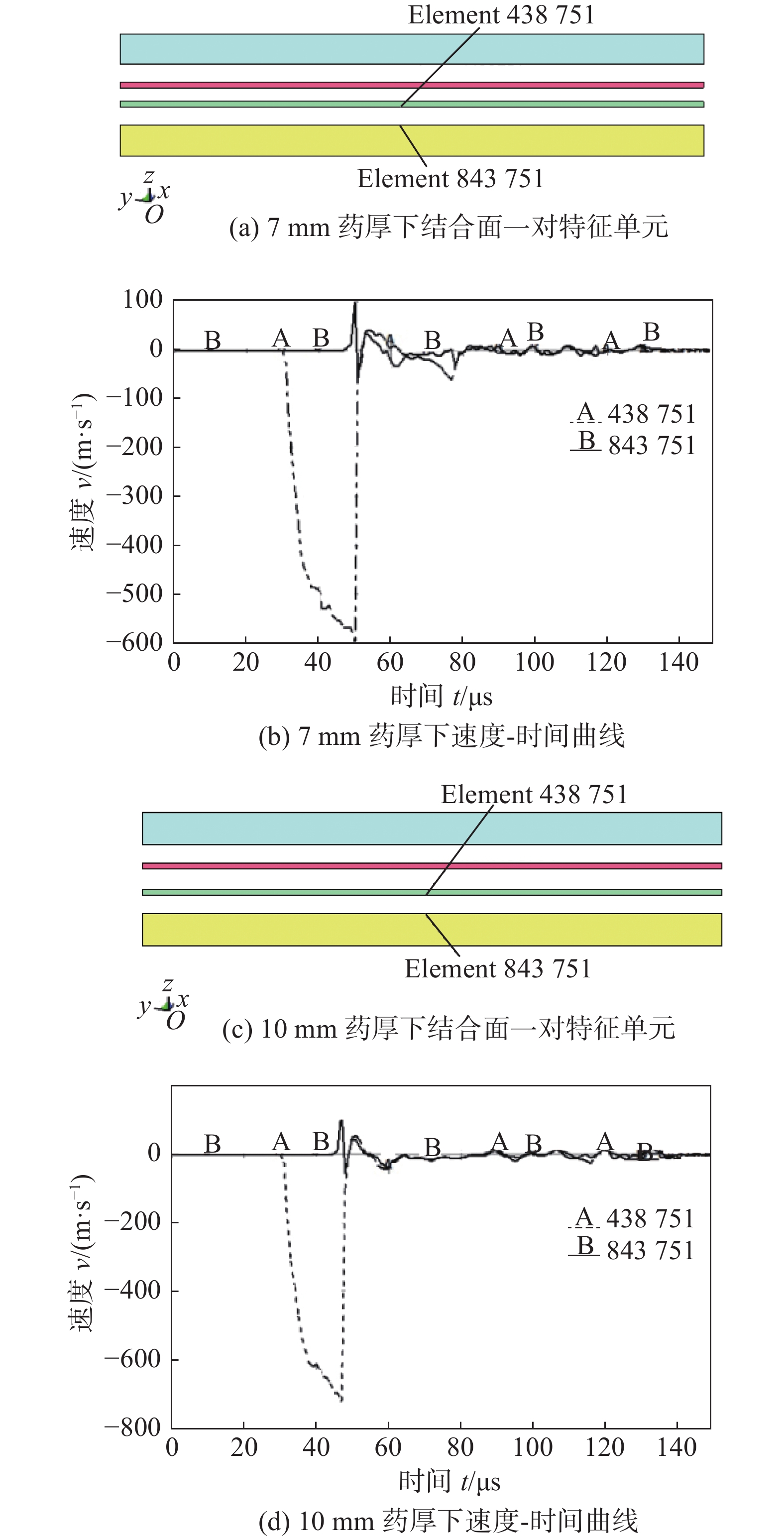
材料 密度ρ/(g·cm−3) 比热容Cp/(J·kg−1·K−1) 热扩散率α/(m2·s−1) 体积声速C0/(m·s−1) 厚度h/m 304不锈钢 7.9 502 3.95×10−6 5790 0.003 Q235钢 7.8 481 2.21×10−5 5200 0.016
下载: 导出CSV
表 5 7 mm药厚碰撞速度的模拟与理论计算
Table 5 Comparison of collision velocity between theoretical calculation and numerical simulation with explosive thickness of 7 mm
质量比 计算结果vcal/(m·s−1) 模拟结果vsim/(m·s−1) 误差比较(%) 0.37 787 595 32.3
下载: 导出CSV
表 6 10 mm药厚碰撞速度的模拟与理论计算
Table 6 Comparison of collision velocity between theoretical calculation and numerical simulation with explosive thickness of 10 mm
质量比 计算结果vcal/(m·s−1) 模拟结果vsim/(m·s−1) 误差比较(%) 0.49 898 723 24.2
下载: 导出CSV
-
[1] Carl L R. Brass welds, made by detonation impulse[J]. Metal Progress, 1944, 46(1): 102 − 103.
[2] 缪广红, 马宏昊, 沈兆武, 等. 不锈钢-普碳钢的双面爆炸复合[J]. 爆炸与冲击, 2015, 35(4): 536 − 540. doi: 10.11883/1001-1455(2015)04-0536-05 Miao Guanghong, Ma Honghao, Shen Zhaowu, et al. Double sided explosive cladding of stainless steel and ordinary carbon steel[J]. Explosion and Shock Waves, 2015, 35(4): 536 − 540. doi: 10.11883/1001-1455(2015)04-0536-05
[3] 缪广红, 马宏昊, 沈兆武, 等. 蜂窝结构炸药及其应用[J]. 含能材料, 2014, 22(5): 693 − 697. Miao Guanghong, Ma Honghao, Shen Zhaowu, et al. Explosives with structure of honeycomb and its application[J]. Chinese Journal of Energetic Materials, 2014, 22(5): 693 − 697.
[4] 史长根, 汪育, 徐宏. 双立爆炸焊接及防护装置数值模拟和试验[J]. 焊接学报, 2012, 33(3): 109 − 112. Shi Changgen, Wang Yu, Xu Hong. Numerical simulation and test of double vertical explosion welding and protective devices[J]. Transactions of the China Welding Institution, 2012, 33(3): 109 − 112.
[5] 史长根, 杨旋, 侯鸿宝, 等. 爆炸焊接两板间距上限法则分析与试验[J]. 焊接学报, 2018, 39(1): 1 − 4. doi: 10.12073/j.hjxb.2018390001 Shi Changgen, Yang Xuan, Hou Hongbao, et al. Analysis and experiment of the upper limit rule of the distance between two plates in explosive welding[J]. Transactions of the China Welding Institution, 2018, 39(1): 1 − 4. doi: 10.12073/j.hjxb.2018390001
[6] Shi Changgen, Sun Zerui, Fang Zhongxing, et al. Design and test of a protective structure for the double vertical explosive welding of large titanium/steel plate[J]. China Welding, 2019, 28(3): 7 − 14.
[7] Zhang Tingting, Wang Wenxian, Zhang Wei, et al. Interfacial microstructure evolution and deformation mechanism in an explosively welded Al/Mg alloy plate[J]. Journal of Materials Science, 2019, 54(12): 9155 − 9167.
[8] Feng Jianrui, Dai Kaida, Zhou Qiang, et al. Formation of bonding interface in explosive welding-a molecular dynamics approach[J]. Journal of Physics, 2019, 31(41): 415403.
[9] Bataev I A, Tanaka S, Zhou Q, et al. Towards better understanding of explosive welding by combination of numerical simulation and experimental study[J]. Materials & Design, 2019, 169: 107649.
[10] 章冠人, 陈大年. 凝聚炸药起爆动力学[M]. 北京: 国防工业出版社, 1991. Zhang Guanren, Chen Danian. Detonation dynamics of condensed explosives[M]. Beijing: National Defence Industry Press, 1991.
[11] 肖定军, 郭学彬, 蒲传金. 单孔护壁爆破数值模拟[J]. 化工矿物与加工, 2008(7): 22 − 24. doi: 10.3969/j.issn.1008-7524.2008.07.007 Xiao Dingjun, Guo Xuebin, Pu Chuanjin. Numerical simulation of single hole wall protection blasting[J]. Chemical Minerals and Processing, 2008(7): 22 − 24. doi: 10.3969/j.issn.1008-7524.2008.07.007
[12] 李裕春, 时党勇, 赵远. ANSYS11.0/LS-DYNA基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008. Li Yuchun, Shi Dangyong, Zhao Yuan. ANSYS11.0/LS-DYNA basic theory and engineering practice[M]. Beijing: China WaterPower Press, 2008.
[13] Liu G R, Liu M B. 光滑粒子流体动力学－一种无网格粒子法[M]. 韩旭译. 长沙: 湖南大学出版社, 2005. Liu G R, Liu M B. Smoothed particle hydrodynamics-a meshfree particle method[M]. Trans.Han Xu. Changsha: Hunan University Press,2005.
[14] 程国强, 李守新. 金属材料在高应变率下的热粘塑性本构模型[J]. 弹道学报, 2004, 11(6): 18 − 22. Cheng Guoqiang, Li Shouxin. Thermal viscoplastic constitutive model of metallic materials at high strain rate[J]. Journal of Ballistics, 2004, 11(6): 18 − 22.
[15] 郑远谋. 爆炸焊接和爆炸复合材料[M]. 北京: 国防工业出版社, 2017. Zheng Yuanmou. Explosive welding and explosive composite material[M]. Beijing: National Defence Industry Press,2017.
[16] 李晓杰. 双金属爆炸焊接上限[J]. 爆炸与冲击, 1991, 4(2): 134 − 138. Li Xiaojie. The upper limit of bimetal explosive welding parameters[J]. Explosion and Shock Waves, 1991, 4(2): 134 − 138.
[17] 缪广红, 李亮, 江向阳, 等. 双面爆炸焊接的数值模拟[J]. 高压物理学报, 2018, 32(4): 1 − 8. Miao Guanghong, Li Liang, Jiang Xiangyang, et al. Numerical simulation of double sided explosive welding[J]. Chinese Journal of High Pressure Physics, 2018, 32(4): 1 − 8.
[18] Saravanan S, Raghukandan K, Hokamoto K. Improved microstructure and mechanical properties of dissimilar explosive cladding by means of interlayer technique[J]. Archives of Civil and Mechanical Engineering, 2016, 16(4): 563 − 568. doi: 10.1016/j.acme.2016.03.009
[19] Nassiri A, Kinsey B. Numerical studies on high-velocity impact welding: smoothed particle hydrodynamics (SPH) and arbitrary Lagrangian-Eulerian(ALE)[J]. Journal of Manufacturing Processes, 2016(24): 376 − 381.
[20] Sui G F, Li J S. Sun F, et al 3D finite element simulation of explosive welding of three-layer plates[J]. Science China, 2011, 54(5): 890 − 896.
[21] Li Yan, Liu Cuirong, Yu Haibo, et al. Numerical simulation of Ti/Al bimetal composite fabricated by explosive welding[J]. Metals, 2017, 7(10): 407.
[22] Findik F. Recent developments in explosive welding[J]. Materials & Design, 2011, 32(3): 1081 − 1093.
[23] Mousavi A, AL-Hassani S T S. Numerical and experimental studies of the mechanism of the wavy interface formations in explosive/impact welding[J]. Journal of the Mechanics and Physics of Solids, 2005, 53(11): 2501 − 2528.
[24] 缪广红, 李亮, 江向阳, 等. 爆炸复合界面波形变化的数值模拟研究[J]. 煤矿爆破, 2017(3): 1 − 4. doi: 10.3969/j.issn.1674-3970.2017.03.001 Miao Guanghong, Li Liang, Jiang Xiangyang, et al. Numerical simulation study on waveform change of explosive composite interface[J]. Coal Mine Blasting, 2017(3): 1 − 4. doi: 10.3969/j.issn.1674-3970.2017.03.001
[25] 王耀华. 金属板材爆炸焊接研究与实践[M]. 北京: 国防工业出版社, 2007. Wang Yaohua. Research and practice of explosive welding of metal plates[M]. Beijing: National Defence Industry Press,2007.
-
期刊类型引用(0)
其他类型引用(2)
计量
- 文章访问数: 395
- HTML全文浏览量: 66
- PDF下载量: 22
- 被引次数: 2
