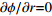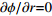Research on arc behavior in gas focusing plasma arc welding
-
摘要: 电弧等离子体行为对焊接接头组织结构和性能具有决定性作用,开展气流再压缩等离子弧特性研究对于指导先进材料的气流再压缩等离子弧焊接工艺和提高焊接接头质量具有重要意义. 针对气流再压缩等离子弧焊接新工艺,基于流体动力学和电磁理论,建立气流再压缩等离子弧数值分析模型,采用ANYSYS Fluent软件,通过C语言进行二次开发,定量计算等离子弧温度分布、流场分布、电势分布,分析压缩气对等离子弧温度场、流场、电弧电压的影响规律. 模拟结果表明,压缩气对喷嘴内的等离子弧温度分布基本没有影响,压缩气对喷嘴外的等离子弧具有拘束压缩作用;压缩气对等离子弧流场分布基本没有影响;压缩气能够提高电弧电压. 相同电流条件下,与常规等离子弧焊接相比,气流再压缩等离子弧焊接电弧穿透能力有望提高.Abstract: Plasma arc behavior plays a decisive role in the microstructure and properties of welded joint. Therefore, it is of great significance to study characteristic of gas focusing plasma for guiding gas focusing plasma arc welding advanced material and improving welded joint properties. The mathematical model of arc in gas focusing plasma arc welding as a new welding process, is developed based on fluid dynamics theory and electromagnetic theory. The model is conducted on software ANSYS Fluent with further development by C program language. The temperature distribution, velocity filed, potential of plasma arc are calculated quantitatively. And influence of focusing gas on arc temperature, plasma velocity and arc voltage is analyzed. Plasma temperature outside of nozzle is focused by focusing gas, while plasma temperature inside of nozzle is basically unchanged with or without focusing gas. Plasma velocity distribution both inside and outside of nozzle has no significant changes with focusing gas. Arc voltage in gas focusing plasma arc welding is larger than that in traditional plasma arc welding with the same welding current. Under the same condition on welding current, arc penetrability in gas focusing plasma arc welding will increase compared with traditional plasma arc welding.
-
Keywords:
- plasma arc welding /
- focusing gas /
- plasma arc behavior /
- temperature field
-
0. 序言
铝锂合金在航天领域主要用于运载火箭推进剂贮箱等部件的焊接制造,采用铝锂合金制造运载器贮箱,可有效降低结构质量,提升运载能力,获得显著的经济效益[1-4]. 目前国外航天型号贮箱结构材料已由最初的铝镁合金、铝铜合金发展到了铝锂合金,其中Weldalite系列的2195铝锂合金应用最为广泛,正逐步取代2A14和2219,用于运载火箭低温贮箱等大型结构[5-6]. 而国内在铝锂合金贮箱结构材料的应用研究方面则相对落后,现阶段仍以2A14和2219材料为主,尚无2195铝锂合金结构件正式应用于产品制造的案例[7].
由于铝锂合金制备常用的熔炼铸造工艺存在缺陷多、成分偏析严重、无法添加更高合金含量等技术瓶颈,使得喷射沉积技术逐渐发展成为铝锂合金材料制备的新途径[8-9]. 喷射沉积技术是将金属雾化熔滴直接成形为具有快速凝固组织特征的材料,所成形的合金材料具有晶粒细小、组织均匀、合金化元素分布均匀、元素过饱和度高且无宏观偏析等显著特点[10-11],尤其适用于含Li以及其它合金元素的高端铝合金制造. 近年来,喷射沉积铝锂合金的研发受到了广泛关注,国内有关单位利用喷射沉积技术已成功制备出2195铝锂合金坯料,并实现了坯料的轧制、挤压、锻造、热处理等工艺的配套. 但从总体上看,目前对喷射沉积2195铝锂合金的焊接研究还处于起步阶段,研究内容主要集中于轧板焊接试验等较为基础的阶段. 于福胜[12]研究了喷射沉积2195-F态铝锂合金的焊接性问题,结果表明,喷射沉积2195-F态铝锂合金轧板的焊接性较好,其焊接接头会发生强化,VPTIG焊和FSW接头拉伸试样均断裂在母材侧. Zhang等人[13]研究了填充焊丝对2195-T6铝锂合金GTAW焊接头组织和力学性能的影响,分别采用铝-铜系和铝-硅-铜系填充焊丝进行了喷射沉积2195铝锂合金轧板的焊接,并讨论了焊丝成分及质量对焊接接头微观组织、力学性能和断裂模式等所造成的影响. 上述研究获得了对喷射沉积2195铝锂合金材料及其焊接性能的基本认识,为该类材料的焊接应用研究进行了有益探索.
2195铝锂合金的主要用途在于结构件制造,在其工程化应用研究过程中,仅仅开展轧板的焊接试验是不够的. 铝锂合金的工程化制造涉及的成形加工方法很多,其大型结构产品的零件常采用旋压、锻造等工艺加工成形,然后将不同成形状态的零件组装焊接在一起,从而构成航空航天类结构级产品. 因此非常有必要研究不同成形状态2195铝锂合金材料的焊接性及接头的组织性能,从而为结构级产品的焊接制造奠定基础.
采用喷射沉积2195铝锂合金旋压件、锻制件制备了焊接试板,采用GTAW工艺进行了“旋压板+锻制板”异种成形状态材料的对接焊,检测了焊接接头的力学性能和维氏硬度,采用电子背散射衍射技术(electron backscattered diffraction, EBSD)对母材及焊接接头进行了微观表征和特征量的统计分析,讨论了喷射沉积2195铝锂合金在经过旋压、锻制不同成形经历后,材料及其焊接接头的微观组织特征与变化情况,从而认识不同成形状态材料GTAW焊接头的组织与性能特点,为喷射沉积2195铝锂合金结构级产品的焊接制造奠定技术基础.
1. 试验材料与方法
1.1 试验材料
使用的材料为喷射沉积2195铝锂合金(记为:SD2195),由江苏豪然喷射成形合金有限公司提供. 试验使用的焊接试板分别取自SD2195材料经旋压和锻制成形后的零件. 其中锻态试板取自SD2195铝锂合金的T6态锻锭,采用机械铣切加工方式制成尺寸为300 mm × 150 mm × 6 mm的焊接试板;旋态试板取自SD2195铝锂合金旋压封头零件,材料旋压前的厚度为13 mm,旋压后的厚度为7 mm,旋压变薄率约为46%. 所取下的试板经修整校平后,再铣切加工成尺寸为300 mm × 150 mm × 6 mm的焊接试板. 填充焊丝采用自主研发的Al-Cu-Zr-Ti系焊丝. 表1为SD2195铝锂合金的主要化学成分,表2为填充焊丝的主要化学成分,表3为SD2195铝锂合金旋、锻态材料的力学性能,表4为SD2195铝锂合金旋、锻态材料微观组织特征的统计结果及与轧板的对比情况. 从表3和表4中的数据可见:SD2195铝锂合金不同的成形经历会直接影响其微观组织和力学性能. 在微观组织方面,锻态和旋态材料的晶粒与轧制态相比都趋于细小并更加均匀. 材料经旋压后变形晶粒的比例很高,达到了92.6%,且变形晶粒细小而均匀,平均晶粒尺寸仅为8.9 μm,标准差为2.1 μm,均明显小于轧态板材;锻态材料的平均晶粒尺寸为10.3 μm,标准差为3.9 μm,同样小于轧态板材,说明SD2195铝锂合金旋、锻态材料的致密性较好. 在力学性能方面,锻态材料的抗拉强度为495 MPa,屈服强度为422 MPa,断后伸长率为9.5%;旋态材料的抗拉强度为475 MPa,屈服强度为420 MPa,断后伸长率为6.5%.
表 1 SD2195铝锂合金主要化学成分(质量分数,%)Table 1. Main chemical compositions of the SD2195 Al-Li alloyCu Mn Mg Ag Si Fe Zr Li Al 3.80 0.000 6 0.45 0.30 0.066 0.035 0.12 0.86 余量 表 2 焊丝的主要化学成分(质量分数,%)Table 2. Main chemical compositions of welding wireCu Si Ti Zr Fe Mn Ag Al 6.44 0.28 0.35 0.26 0.080 0.001 1 0.35 余量 表 3 SD2195铝锂合金旋、锻态母材力学性能Table 3. Mechanical properties of SD2195 Al-Li alloy in spinning and forged states材料状态 抗拉强度Rm/MPa 屈服强度ReL/MPa 断后伸长率A(%) 锻制板-T6 495 422 9.5 旋压板-T6 490 437 6.5 表 4 SD2195铝锂合金不同成形状态母材微结构特征量的统计对比Table 4. Statistics and comparison of microstructure features of SD2195 Al-Li alloy in different forming states材料状态 再结晶晶粒比例δ1(%) 亚结构晶粒比例δ2(%) 变形晶粒比例δ3(%) 小角度晶界比例δ4(%) 平均晶粒尺寸(标准差)d/μm 锻制板-T6 16.5 7.1 76.4 30.1 10.3(3.9) 旋压板-T6 7.1 0.3 92.6 33.6 8.9(2.1) 轧板- T6(对比) 6.1 13.2 80.7 25.4 12.5(8.9) 1.2 试验方法
如图1所示,焊接试验采用单面两层GTAW焊工艺,焊接坡口采用95° V形坡口,留1 ~ 1.5 mm钝边,焊接装配间隙约为1.5 mm. 焊接前严格清理试板表面,采用整体酸洗、机械打磨待焊接位置和酒精清洗等方式进行,尽可能避免焊接气孔及氧化物夹杂等缺陷. 焊接设备为林肯Precision TIG 375焊机,焊接过程中采用双面氩气保护的方式,在板的背面和焊枪处均提供氩气保护,尽可能防止焊接氧化. 试验中为使焊缝成形良好,在打底焊接时选用大电流和小电压以提供较大的电弧力从而使试板熔透,在盖面焊接时选用小电流和大电压以使电弧能够铺展从而保证覆盖住打底焊缝并成形良好,打底层焊接电流为210 ~ 230 A,焊接电压为16.5 ~ 17.5 V,焊接速度为130 ~ 140 mm/min;盖面层焊接电流为180 ~ 200 A,焊接电压为17.5 ~ 18.5 V,焊接速度为120 ~ 130 mm/min. 试样焊接完成后,按照GB/T 16865—2013《变形铝、镁及其合金加工制品拉伸试验用试样及方法》加工拉伸试样(共3件试样,试样标距为50 mm),并进行了接头的拉伸性能试验. 按照GB/T 4340《金属材料维氏硬度试验》进行了接头维氏硬度检测,使用金相显微镜观察了接头各区域的金相组织,使用扫描电镜观察了拉伸试样断口形貌. 采用EBSD技术表征了接头微观组织,并进行了主要特征量的统计计算. 在此基础上,分析讨论了SD2195铝锂合金旋、锻态材料及其焊接接头的微观组织结构特征与变化情况,从而认识SD2195铝锂合金异种成形状态材料GTAW焊接头的组织与性能.
2. 试验结果与分析
2.1 微观组织特征
图2为旋-锻态接头的金相组织,其中图2a,2b,2c和图2d,2e,2f分别为锻侧和旋侧接头的焊缝区(WZ)、熔合区(FZ)和焊接热影响区(HAZ). 从图中可见,锻侧与旋侧的焊接热影响区基本保持了母材的“带状”组织特征,并出现了晶粒轻微长大的现象. 自焊接热影响区至熔合区逐渐产生了再结晶,且过渡区域结合良好,焊缝区总体上呈现出细小的等轴晶特征.
图3为旋-锻态接头焊缝区的再结晶分布图及晶粒与晶界分布图. 再结晶分布图中,红色表示变形晶粒组织,黄色表示亚结构晶粒组织,蓝色表示再结晶晶粒组织. 在变形晶粒组织中,合金晶内和晶界均有很高的位错密度. 亚结构晶粒内部有较低的位错密度,晶界有较高的位错密度. 再结晶晶粒由于发生再结晶导致晶粒内部和晶界位错密度很低. 由图可见,旋-锻态接头焊缝区打底层金属在较高的热力学环境下,合金再结晶驱动力增大,再结晶晶粒尺寸增大. 同时,由于也导致了打底层金属位错密度降低,晶粒主要以亚结构晶粒组织和再结晶晶粒组织形式存在,而盖面金属主要以再结晶晶粒存在.
根据晶体结构中相邻晶粒的晶界位向差(角度),可以将晶界分为小角度晶界和大角度晶界两种类型. 在图3晶界分布图中,红色表示小角度晶界(取向差角不大于15°),黑色表示大角度晶界(取向差角大于15°). 盖面区域有相对较高比例的小角度晶界,而打底区域有比例略高的大角度晶界. 由于焊缝区金属为“欠固溶”的铸态组织,焊缝金属中存在着大量的黑色线条表示的大角度晶界,其小角度晶界比例不高,如靠近旋侧的焊缝金属小角度晶界比例仅为6.4%,靠近锻侧的焊缝金属小角度晶界比例仅为7.8%. 晶界取向角的物理属性以及对材料性能分析的意义可通过对位错能量与位错密度的分析来说明. 相关研究表明[14-16],在变形过程中,小角度晶界通常表现出较好的塑性应变兼容性,能够对裂纹产生阻碍作用,裂纹通常在大角度晶界上萌生和扩展. 小角度晶界的界面能比大角度晶界低,在受外力加载的过程中,根据能量最低原理可知,大角度晶界是相对的薄弱区域,易成为缺陷优先产生的位置. 因此与各自母材相比,焊缝的小角度晶界比例均偏低,这就从冶金组织的角度能够解释焊缝区在接头力学性能上处于“弱势”的原因.
2.2 微观组织特征
表5为旋-锻态接头旋侧和锻侧的微观组织特征统计结果. 如1.1节所述,旋态和锻态母材都有变形晶粒比例略高的特点,经焊接的两次热循环过程后,旋态和锻态的焊接热影响区均出现与母材不同的微观组织晶粒特点. 焊接后变形晶粒被无畸变的等轴晶粒逐渐替代,再结晶组织晶粒比例增加. 从表5与表4中的数据对比可见,旋态母材焊缝侧的再结晶晶粒比例由7.1%增加至23.9%,锻态母材焊缝侧的再结晶晶粒比例由16.5%增加至18.9%. 旋态母材变形晶粒的转变量高于锻态,应与其晶粒内形变驱动能较大有关. 图4为锻态与旋态母材、焊接熔合区、焊缝区的KAM图. KAM图可反映位错密度的分布[17],按“蓝-绿-黄-橙-红”表示由小到大. 由图可见,旋态母材的位错密度明显高于锻态母材,说明旋压材料内部存在着更大的应力储能. 由于旋态母材是经冷塑性加工成形(旋压成形)而获得的,旋压形变量较大(旋压减薄率约为46%),其内部存在较多数量的机械储能,在焊接受热时提供了较大的再结晶驱动力. 在接头熔合区和焊缝区等变形晶粒组织较多的区域,旋态和锻态材料的位错密度均逐渐降低. 晶粒间的这种转变,将造成母材热影响区出现“回复再结晶”软化现象,一方面导致了晶粒组织长大和各项异向性增大,发生塑性变形时所需克服的位错堆积阻力变弱,造成拉伸强度下降;另外也导致了旋、锻侧母材HAZ区域合金位错密度降低,使合金发生塑性变形所需的晶界上位错堆叠需求量增大,材料的塑性得以提升,而断后伸长率得到了明显提升.
表 5 旋-锻态接头微结构特征量统计Table 5. Statistics of microstructural characteristics of spun-forged joint材料状态/表征位置 再结晶晶粒比例δ1(%) 亚结构晶粒比例δ2(%) 变形晶粒比例δ3(%) 小角度晶界比例δ4(%) 平均晶粒尺寸(标准差)d/μm 旋侧-母材(HAZ) 23.9 5.2 60.9 22.3 11.8(6.8) WM(均值) 51.3 42.3 6.5 6.4 22.5(9.9) FZ(均值) 41.6 10.9 47.5 24.5 16.2(8.2) 锻侧-母材(HAZ) 18.9 9.4 71.7 27.5 15.4(9.4) WM(均值) 29.9 59.9 10.3 7.8 24.9(9.9) FZ(均值) 35.3 37.2 27.6 29.1 22.6(10.7) 图5为锻、旋态材料从母材到焊接接头的晶粒尺寸的演变经历,其中黑点表示平均晶粒尺寸,黑色横线在长度方向上表示晶粒尺寸的变化幅度. 结合表5中的数据,可见晶粒尺寸及其变化特点:一是当材料经T6处理后,两种状态材料的平均晶粒尺寸均在10 μm左右;当材料经历了焊接热循环之后,两种状态材料热影响区的平均晶粒尺寸均处于10 ~ 15 μm的水平,与各自的原始态(退火处理状态,退火参数为:退火温度425 ℃ ± 3 ℃,保温2 h;随炉冷却35 ~ 40 min,降至260 ℃空冷)的平均晶粒尺寸相当. 二是旋态母材晶粒尺寸的分散性(即标准差)较小,在材料经过较大形变量的旋压成形加工后,所形成的旋态材料晶粒更为细小且均匀,经过打底及盖面焊接两次热循环,其晶粒尺寸及分布特征仍得以保持,与锻侧接头相比,旋态接头热影响区和熔合区的平均晶粒尺寸及标准差均相对较小. 三是旋、锻态接头焊接熔合区的平均晶粒尺寸均在15 ~ 23 μm范围内,与对应的焊缝平均晶粒尺寸20 ~ 25 μm的尺寸已相当匹配,说明组织已具有较好的“连续性”,这对改善焊接接头的综合性能是非常有利的.
2.3 力学性能分析
表6为旋-锻态接头的力学性能检测结果. 对应于上述对微观组织及主要特征量的统计分析结果,焊接接头的抗拉强度平均值(339 MPa)分别达到了旋态母材的71%和锻态母材的68%,断后伸长率平均值达到了7.3%. 其中,拉伸试样断裂位置分别在锻态母材的热影响区、接头熔合线的锻态焊缝侧和旋态母材的热影响区,接头力学性能较高且断裂位置较为分散,说明了该焊接接头组织具有较好的综合性能.
表 6 旋-锻态接头力学性能及与母材的对比Table 6. Mechanical properties of the spun-forged joint and comparison with base metal接头/材料状态 抗拉强度Rm/MPa 抗拉强度均值$\overline {{R_{\rm{m}}}} $/MPa 断后伸长率A(%) 断后伸长率均值$\overline A $(%) 备注 旋-锻态接头 341 339 8.0 7.3 1号试样,断裂于锻侧HAZ 338 6.0 2号试样,断裂于锻侧熔合线 337 8.0 3号试样,断裂于旋侧HAZ 旋态母材(对比) 475 6.5 3个试样均值 锻态母材(对比) 495 9.5 3个试样均值 图6为旋-锻态接头的硬度分布情况. 在焊接接头横截面上进行了两排的维氏硬度测试,检测位置分别距离试板底边1.5和4.5 mm,从焊缝中心开始,每2个临近点的距离是0.5 mm,试验的加载力为500 gf,保留载荷时间为10 s. 由图可见,接头硬度总体上是以焊缝中心线为对称轴呈近似对称分布,接头焊缝区的硬度较低,旋侧与锻侧熔合区及热影响区的硬度分布基本一致,焊接热循环对旋、锻侧母材热影响区性能造成了明显影响,即在距焊缝中心15 mm左右的旋、锻态母材均出现了明显的软化现象,从而导致母材强度性能的下降,而断后伸长率得到了相应提高,这与旋、锻态母材热影响区不同程度出现的变形晶粒转变为亚结构晶粒和再结晶晶粒的特征变化相符.
图7为旋-锻态接头拉伸试样断裂于锻侧熔合线(2号试样)和热影响区(1号试样)的断口形貌. 图7a和图7b分别是熔合线打底层和盖面层的断口形貌,前者的韧窝小而浅,且分布不均匀,主要以韧性断裂为主,而盖面层的熔合线断口韧窝比打底层大且均匀,具有完全的韧性断裂特征;与断裂在焊接热影响区的断口形貌相比(图7c),后者的断口一次韧窝大而深,并包含较多的二次韧窝,表明该断口具有较好的韧性,相应的断后伸长率已与母材接近.
从喷射沉积2195铝锂合金旋、锻态材料及焊接接头的微观组织特征和力学性能来看,喷射沉积材料自身快速凝固特性所带来的初始晶粒细小、成分均匀等基因性特点在其焊接过程中得到了延续,焊接接头的宏观力学性能较好. 一方面,接头焊缝的晶粒细小而均匀,起到了明显的细晶强化作用. 依据多晶体塑性变形理论,多晶体在塑性变形过程中,由于晶界处原子排列紊乱、畸变能高,且晶界两边晶粒的取向不同,滑移难以从一个晶粒内直接传播至另一个晶粒内[18]. 因此,位错滑移在晶内进行时较为容易,而越过晶界的难度相对较大. 如同一体积内的焊缝晶粒越细,则晶粒数量就越多,晶界所占的体积分数也就相应增大,位错滑移进行的难度就更大,焊缝的强度就会相应提高. 另一方面,焊接接头各区域的组织“连续性”较好,通过采用合理的焊接工艺,能够实现该类材料焊接接头各区域具有较好的组织均匀性,从而提高接头的综合力学性能,一定程度上展现了喷射沉积铝锂合金材料应用于焊接结构制造的优势.
3. 结论
(1) SD2195铝锂合金材料经过锻造、旋压等加工经历后,材料的致密性较好,T6态锻制及旋压材料晶粒相比于轧板材料更为细小和均匀,平均晶粒尺寸分别为10.3,8.9 μm,标准差分别为3.9,2.1 μm.
(2) SD2195铝锂合金旋态及锻态材料具有良好的GTAW焊工艺性,旋-锻态接头的抗拉强度均值达到了各自母材的71%和68%,断后伸长率均值达到7.3%,拉伸断口呈现出明显的韧性断裂特征.
(3) 在经历了焊接热循环后,旋-锻态接头焊缝区金属小角度晶界比例较低,旋侧的小角度晶界比例仅为6.4%,锻侧的小角度晶界比例仅为7.8%;旋侧与锻侧的焊接热影响区及熔合区均趋于一种相似的微结构,母材、热影响区、熔合区及焊缝金属的平均晶粒尺寸依次处于10,10 ~ 15,15 ~ 23,20 ~ 25 μm的水平,说明组织具有较好的“连续性”,材料初始晶粒细小、成分均匀等特点在后续焊接过程中得到了有效保持.
-
表 1 GF-PAW电弧数值模拟边界条件
Table 1 Boundary conditions of arc modeling in GF-PAW
边界名称 轴向速度vz/(m·s−1) 径向速度vr/(m·s−1) 温度T/K 电势 $\phi $ /V相对压强ρ/Pa BC 常数 0 1000 $\scriptstyle{ {\partial \phi } / {\partial r = 0} }$ ─ CKLD 0 0 1000 $\scriptstyle{ {\partial \phi } / {\partial r = 0} }$ DE 常数 0 300 $\scriptstyle{ {\partial \phi } / {\partial r = 0} }$ ─ EF 0 0 1000 $\scriptstyle{ {\partial \phi } / {\partial r = 0} }$ ─ FG 常数 0 1000 $\scriptstyle{ {\partial \phi } / {\partial r = 0} }$ ─ GH 0 0 1000 $\scriptstyle{ {\partial \phi } / {\partial r = 0} }$ 0 HI 0 0 3000 0 ─ IO ${v_z}$ $\scriptstyle{ {\partial {v_r} } / {\partial r = 0} }$ $\scriptstyle{ {\partial T}/ {\partial r = 0} }$ $\scriptstyle{ {\partial \phi }/ {\partial r = 0} }$ ─ OJ 0 0 3500 $- \scriptstyle\sigma \left( { { {\partial \phi } / {\partial r} } } \right) = {I / {\pi {r^2} } }$ ─ BMJ 0 0 3000 $\scriptstyle{ {\partial \phi } / {\partial r = 0} }$ ─ 表 2 主要焊接工艺参数
Table 2 Welding parameter
焊接方法 焊接电流
I/A离子气流量 QP/(L·min−1) 压缩气流量QF/(L·min−1) 保护气流量QS/(L·min−1) PAW 140 2.0 0 20 GF-PAW 140 2.0 1.0 20 -
[1] 孙俊生, 武传松. 双面电弧焊接的传热模型[J]. 物理学报, 2002, 51(2): 286 − 290. doi: 10.3321/j.issn:1000-3290.2002.02.015 Sun Junsheng, Wu Chuansong. Heat transfer modeling of double-side arc welding[J]. Acta Physica Sinica, 2002, 51(2): 286 − 290. doi: 10.3321/j.issn:1000-3290.2002.02.015
[2] Vredeveldt H L. Increased power density plasma arc welding: the effect of an added radial gas flow around the arc root[D]. Delft: Technische Universiteit Delft, 2014.
[3] Nguyen V A, Shinichi T, Bui V H, et al. Experimental investigation on the weld pool formation process in plasma keyhole arc welding[J]. Journal of Physics D: Applied Physics, 2018, 51(1): 14 − 50.
[4] Wu C S, Zhao C Y, Zhang C, et al. Ultrasonic vibration-assisted keyholing plasma arc welding[J]. Welding Journal, 2017, 96(8): 279 − 286.
[5] Wu C S, Wang L, Ren W J, et al. Plasma arc welding: process, sensing, control and modeling[J]. Journal of Manufacturing Processes, 2014, 16(1): 74 − 85. doi: 10.1016/j.jmapro.2013.06.004
[6] 胡庆贤, 徐斌, 王晓丽, 等. 穿孔型等离子弧焊接热-力耦合模型优化[J]. 焊接学报, 2017, 38(1): 13 − 16. Hu Qingxian, Xu Bin, Wang Xiaoli, et al. Optimization of thermal mechanical coupled model of K-PAW[J]. Transactions of the China Welding Institution, 2017, 38(1): 13 − 16.
[7] 张涛, 武传松, 陈茂爱. 穿孔等离子弧焊接熔池流动和传热过程的数值模拟[J]. 金属学报, 2012, 48(9): 1025 − 1032. doi: 10.3724/SP.J.1037.2012.00147 Zhang Tao, Wu Chuansong, Chen Maoai. Modelling fluid flow and heat transfer phenomena in keyholing stage of plasma arc welding[J]. Acta Metallurgica Sinica, 2012, 48(9): 1025 − 1032. doi: 10.3724/SP.J.1037.2012.00147
[8] Li X R, Heusman J, Kvidahl L, et al. Manual keyhole plasma arc welding with application[J]. Welding Journal, 2011, 90(12): 258 − 264.
[9] Chen S J, Zhang R Y, Jiang F, et al. A novel method for testing the electrical property of arc column in plasma arc welding[J]. Welding in the World, 2018, 62(3): 637 − 645. doi: 10.1007/s40194-018-0561-2
[10] Li Y, Feng Y, Zhang X, et al. Energy propagation in plasma arc welding with keyhole tracking[J]. Energy, 2014, 64(1): 1044 − 1056.
[11] Zhang G K, Wu C S, Liu X F. Single vision system for simultaneous observation of keyhole and weld pool in plasma arc welding[J]. Journal of Materials Processing Technology, 2015, 215(1): 71 − 78.
[12] Li T Q, Wu C S, Feng Y H, et al. Modeling of the thermal fluid flow and keyhole shape in stationary plasma arc welding[J]. International Journal of Heat and Fluid Flow, 2012, 34: 117 − 125. doi: 10.1016/j.ijheatfluidflow.2011.12.004
[13] Li T Q, Wu C S. An analytic formula describing the plasma arc pressure distribution[J]. China Welding, 2014, 23(2): 7 − 11.
[14] Li T Q, Wu C S. Numerical simulation of plasma arc welding with keyhole-dependent heat source and arc pressure distribution[J]. The International Journal of Advanced Manufacturing Technology, 2015, 78(1): 593 − 602.
[15] Li T Q, Wu C S, Chen J. Transient variation of arc heat flux and pressure distribution on keyhole wall in PAW[J]. Welding in the World, 2016, 60(2): 363 − 371. doi: 10.1007/s40194-015-0290-8
[16] Cai J J, Feng Y H, Zhou J J, et al. Numerical analysis of weld pool behaviors in plasma arc welding with the lattice Boltzmann method[J]. International Journal of Thermal Sciences, 2018, 124: 447 − 458. doi: 10.1016/j.ijthermalsci.2017.10.026
[17] 陈树君, 徐斌, 蒋凡. 变极性等离子弧焊电弧物理特性的数值模拟[J]. 金属学报, 2017, 53(5): 631 − 640. doi: 10.11900/0412.1961.2016.00263 Chen Shujun, Xu Bin, Jiang Fan. Numerical simulation of physical characteristics of variable polarity plasma arc welding[J]. Acta Metallurgica Sinica, 2017, 53(5): 631 − 640. doi: 10.11900/0412.1961.2016.00263
[18] 吴宣楠, 冯妍卉, 李岩, 等. 穿孔等离子弧焊接弧与熔池的耦合模拟及正交分析[J]. 金属学报, 2015, 51(11): 1365 − 1376. Wu Xuannan, Feng Yanhui, Li Yan, et al. Numerical simulation and orthogonal analysis on coupled arc with molten pool for keyholing plasma arc welding[J]. Acta Metallurgica Sinica, 2015, 51(11): 1365 − 1376.
[19] 菅晓霞, 武传松. Fe蒸汽对等离子弧焊接熔池行为的影响[J]. 金属学报, 2016, 52(11): 1467 − 1476. Jian Xiaoxia, Wu Chuansong. Influence of Fe vapour on weld pool behavior of plasma arc welding[J]. Acta Metallurgica Sinica, 2016, 52(11): 1467 − 1476.
[20] Chen J, Wu C S, Jian X X, et al. A unified 3D model for an interaction mechanism of the plasma arc, weld pool and keyhole in plasma arc welding[J]. Journal of Physics D: Applied Physics, 2015, 48(46): 1 − 14.
[21] 李天庆, 杨喜牟, 雷玉成, 等. 气流再压缩等离子弧焊接工艺初步研究[J]. 焊接学报, 2019, 40(11): 28 − 32. doi: 10.12073/j.hjxb.2019400283 Li Tianqing, Yang Ximou, Lei Yucheng, et al. An initial study on gas focusing plasma arc welding process[J]. Transactions of the China Welding Institution, 2019, 40(11): 28 − 32. doi: 10.12073/j.hjxb.2019400283
[22] Hsu K C. A self-consistent model for the high intensity free-burning argon arc[D]. Minneapolis: University of Minnesota, 1982.
[23] Cram E L. Statistical evaluation of radiative power losses from thermal plasmas due to spectral lines[J]. Journal of Physics D: Applied Physics, 1985, 18(3): 401 − 411. doi: 10.1088/0022-3727/18/3/009



 下载:
下载: